Area Of A Cylinder With Diameter
listenit
Mar 31, 2025 · 4 min read
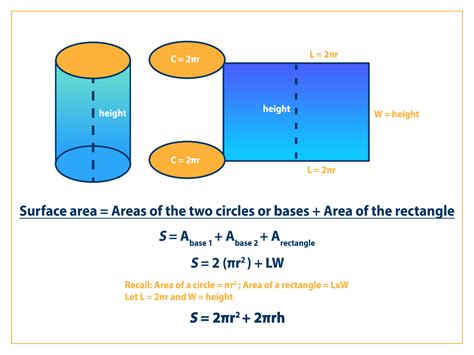
Table of Contents
Calculating the Area of a Cylinder Using Diameter: A Comprehensive Guide
Understanding how to calculate the surface area of a cylinder is a crucial skill in various fields, from engineering and architecture to manufacturing and design. While formulas often use the radius, knowing how to work with the diameter simplifies the process, especially when dealing with real-world measurements where diameter is more readily available. This comprehensive guide breaks down the calculation process, exploring the different components of a cylinder's surface area and offering practical examples and troubleshooting tips.
Understanding Cylinder Geometry and its Components
A cylinder is a three-dimensional geometric shape characterized by two parallel circular bases connected by a curved lateral surface. Key components influencing the surface area calculation include:
- Diameter (d): The distance across the circle through its center. This is often the measurement readily available in practical applications.
- Radius (r): Half the diameter (r = d/2). The radius is crucial for many geometric formulas, but we'll show how to use diameter directly.
- Height (h): The perpendicular distance between the two circular bases.
Calculating the Total Surface Area of a Cylinder Using Diameter
The total surface area of a cylinder is the sum of the areas of its two circular bases and its curved lateral surface. Here’s how to calculate it using the diameter:
1. Area of the Circular Bases:
Each circular base has an area calculated using the formula: A_base = πr²
Since r = d/2, we can substitute this into the formula:
A_base = π(d/2)² = πd²/4
Because there are two bases, the total area of the bases is:
2 * A_base = 2 * (πd²/4) = πd²/2
2. Area of the Lateral Surface:
The lateral surface area is the area of the curved side of the cylinder. Imagine unrolling this surface; it forms a rectangle with a width equal to the cylinder's height (h) and a length equal to the circumference of the base (C).
The circumference of the base is C = πd.
Therefore, the lateral surface area is:
A_lateral = h * C = h * πd
3. Total Surface Area (TSA):
The total surface area is the sum of the areas of the two bases and the lateral surface:
TSA = A_bases + A_lateral = πd²/2 + πdh
This concise formula allows us to calculate the total surface area using only the diameter (d) and the height (h) of the cylinder.
Step-by-Step Example: Calculating the Surface Area
Let's consider a cylinder with a diameter of 10 cm and a height of 15 cm. Let's calculate its total surface area step by step:
1. Calculate the area of the bases:
A_bases = πd²/2 = π(10 cm)²/2 = 50π cm² ≈ 157.08 cm²
2. Calculate the lateral surface area:
A_lateral = πdh = π(10 cm)(15 cm) = 150π cm² ≈ 471.24 cm²
3. Calculate the total surface area:
TSA = A_bases + A_lateral = 50π cm² + 150π cm² = 200π cm² ≈ 628.32 cm²
Therefore, the total surface area of the cylinder is approximately 628.32 square centimeters.
Practical Applications and Real-World Scenarios
The ability to calculate the surface area of a cylinder using the diameter has numerous practical applications:
- Packaging Design: Determining the amount of material needed to manufacture cylindrical containers for products.
- Civil Engineering: Calculating the surface area of cylindrical pillars or pipes for coating or painting estimates.
- Manufacturing: Estimating the material required for manufacturing cylindrical components in various industries.
- Architectural Design: Calculating the surface area of cylindrical structures in building design for material estimations and cost analysis.
- Robotics and Automation: Programming robotic arms to manipulate cylindrical objects accurately requires understanding surface area for gripping and manipulation.
Troubleshooting Common Mistakes
Several common mistakes can lead to inaccurate calculations. Here are some points to keep in mind:
- Units: Ensure consistent units throughout the calculation (e.g., all measurements in centimeters or inches).
- Diameter vs. Radius: Remember to use the correct value – the diameter – in the formulas presented above. Avoid accidentally using the radius instead.
- Order of Operations: Follow the order of operations (PEMDAS/BODMAS) correctly when calculating the area. Squaring the diameter should be done before multiplication with π.
- Approximation of π: The value of π is approximately 3.14159. Using a more precise value of π will yield a more accurate result, especially in applications requiring high precision.
Advanced Concepts and Extensions
This fundamental understanding can be extended to more complex scenarios:
- Hollow Cylinders: For hollow cylinders, you'll need to calculate the surface area of the inner and outer cylinders separately and consider the difference.
- Cylindrical Sections: Calculating the surface area of partial cylinders requires integrating calculus techniques.
- Non-Right Cylinders: If the cylinder's axis is not perpendicular to the bases (oblique cylinder), the calculation becomes more complex, often requiring vector calculus.
Conclusion: Mastering Cylinder Surface Area Calculations
Calculating the surface area of a cylinder using the diameter streamlines the process and offers a practical approach for various real-world applications. By understanding the formulas, following the steps carefully, and paying attention to detail, you can accurately determine the surface area, crucial for numerous engineering, design, and manufacturing processes. This guide provides a comprehensive foundation to confidently tackle surface area calculations and solve related problems efficiently. Remember to always double-check your work and utilize appropriate tools for accurate calculations, especially in scenarios where precision is paramount.
Latest Posts
Latest Posts
-
What Is It Called When Homologous Chromosomes Exchange Genes
Apr 02, 2025
-
Whats The Square Root Of 39
Apr 02, 2025
-
What Is The Square Root Of 122
Apr 02, 2025
-
The Unit Of Energy In Si Units Is
Apr 02, 2025
-
How To Find The Mean Of A Probability Distribution
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Area Of A Cylinder With Diameter . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
