A Parallelogram Is Always A Rectangle
listenit
Apr 02, 2025 · 5 min read
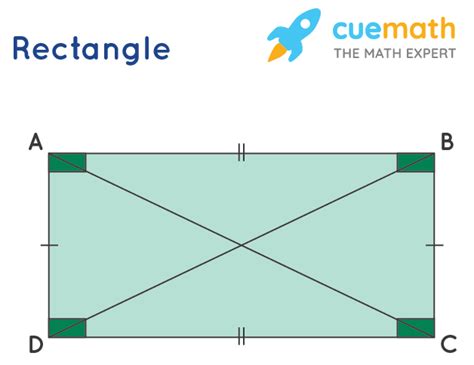
Table of Contents
A Parallelogram is Always a Rectangle: Exploring the Relationship Between Shapes
The statement "a parallelogram is always a rectangle" is false. While rectangles possess all the properties of parallelograms, the reverse is not true. This article delves into the defining characteristics of both parallelograms and rectangles, highlighting the key differences that prevent a parallelogram from automatically qualifying as a rectangle. Understanding these distinctions is crucial for mastering geometric concepts and problem-solving in various mathematical contexts.
Defining Parallelograms
A parallelogram is a quadrilateral (a four-sided polygon) characterized by two pairs of parallel sides. This fundamental property leads to several other important characteristics:
- Opposite sides are equal in length: This directly stems from the parallel sides.
- Opposite angles are equal: The angles opposite each other are congruent.
- Consecutive angles are supplementary: This means that the sum of any two adjacent angles is 180 degrees.
- Diagonals bisect each other: The diagonals intersect at their midpoints.
These properties are essential for identifying and working with parallelograms in various geometric proofs and applications. Understanding these features allows us to solve problems related to area, perimeter, and angle calculations involving parallelograms.
Defining Rectangles
A rectangle is a specific type of parallelogram with additional defining features:
- All angles are right angles (90 degrees): This is the crucial difference between a parallelogram and a rectangle. While a parallelogram only requires parallel sides, a rectangle demands that all its interior angles be right angles.
- Opposite sides are equal in length: Rectangles inherit this property from parallelograms.
- Diagonals bisect each other: Like parallelograms, the diagonals of a rectangle bisect each other. However, in a rectangle, the diagonals are also equal in length.
The presence of right angles significantly impacts the properties and applications of rectangles. This additional constraint allows for simpler calculations, particularly regarding area (length x width) and diagonal lengths (using the Pythagorean theorem).
Why a Parallelogram Isn't Always a Rectangle: Counterexamples
The most compelling way to demonstrate that a parallelogram is not always a rectangle is to present counterexamples. Consider the following scenarios:
Scenario 1: The Oblique Parallelogram
Imagine a parallelogram with its sides forming acute and obtuse angles. This parallelogram clearly fulfills the definition of a parallelogram (parallel opposite sides), but its angles are not 90 degrees. Therefore, it fails to meet the requirements of a rectangle.
Scenario 2: The Rhomboid
A rhomboid is a parallelogram with unequal adjacent sides. Again, it satisfies the definition of a parallelogram, exhibiting parallel opposite sides. However, its angles are not necessarily right angles, meaning it does not qualify as a rectangle.
Scenario 3: A Parallelogram with Diagonals of Unequal Lengths
In a rectangle, the diagonals are always equal in length. If we draw a parallelogram where the diagonals are of unequal lengths, this immediately disqualifies it from being a rectangle.
These examples definitively showcase that the property of having parallel sides is insufficient to guarantee the existence of right angles. The defining characteristic of a rectangle – the presence of four right angles – is what distinguishes it from a broader category of parallelograms.
Exploring the Hierarchy of Quadrilaterals
To further understand the relationship between parallelograms and rectangles, it's helpful to visualize the hierarchy of quadrilaterals:
- Quadrilaterals: The broadest category, encompassing all four-sided polygons.
- Parallelograms: A subset of quadrilaterals with two pairs of parallel sides. This includes rectangles, rhombi, and squares.
- Rectangles: A subset of parallelograms with four right angles. This also includes squares.
- Rhombi (Rhombuses): A subset of parallelograms with all four sides equal in length. This includes squares.
- Squares: A subset of both rectangles and rhombi, possessing both four right angles and four equal sides.
This hierarchical structure clarifies that a rectangle is a special case of a parallelogram, inheriting all parallelogram properties, but with the added condition of right angles. Therefore, while all rectangles are parallelograms, not all parallelograms are rectangles.
Practical Applications and Problem Solving
The distinctions between parallelograms and rectangles have practical implications in various fields:
- Engineering and Construction: The properties of rectangles are fundamental in structural design and building construction. Rectangular shapes offer stability and simplify calculations related to area and volume.
- Computer Graphics and Game Design: Rectangles and squares are widely used in creating and manipulating graphical elements in computer applications. Understanding their geometric properties is crucial for accurate rendering and positioning.
- Cartography and Surveying: Parallelograms and rectangles appear in various map projections and land surveying techniques. The understanding of their properties facilitates accurate measurements and calculations.
- Physics and Engineering: Parallelograms and rectangles find applications in resolving vectors and analyzing forces in physics and engineering problems.
Advanced Concepts and Further Exploration
The study of parallelograms and rectangles extends beyond their basic definitions:
- Vectors and Coordinate Geometry: Using vector methods and coordinate geometry helps analyze the properties of parallelograms and rectangles in more advanced mathematical settings.
- Transformations and Symmetry: Exploring the effects of transformations (rotations, reflections, translations) on parallelograms and rectangles provides valuable insights into their geometric properties and symmetries.
- Non-Euclidean Geometry: The properties of parallelograms and rectangles can also be explored in the context of non-Euclidean geometries, where the parallel postulate of Euclidean geometry does not hold.
Conclusion: A Refined Understanding of Geometric Shapes
The assertion "a parallelogram is always a rectangle" is fundamentally incorrect. While all rectangles are parallelograms, the reverse is not true. The crucial distinction lies in the presence of four right angles in rectangles, a characteristic not required for parallelograms. Understanding this difference is pivotal for accurately applying geometric principles in problem-solving and diverse real-world applications. Through this detailed exploration, we have developed a more nuanced and complete understanding of these fundamental geometric shapes and their interconnected relationships. The hierarchical structure of quadrilaterals, highlighted through examples and scenarios, firmly establishes the distinct nature of parallelograms and rectangles, facilitating a deeper grasp of geometric concepts.
Latest Posts
Latest Posts
-
1 Over 5 As A Decimal
Apr 03, 2025
-
60 Percent Of 40 Is What Number
Apr 03, 2025
-
How Does Friction Affect An Objects Motion
Apr 03, 2025
-
How Many Gallons In 12 Pints
Apr 03, 2025
-
Whats The Derivative Of A Constant
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about A Parallelogram Is Always A Rectangle . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
