9k - 5 + K + 3
listenit
May 09, 2025 · 5 min read
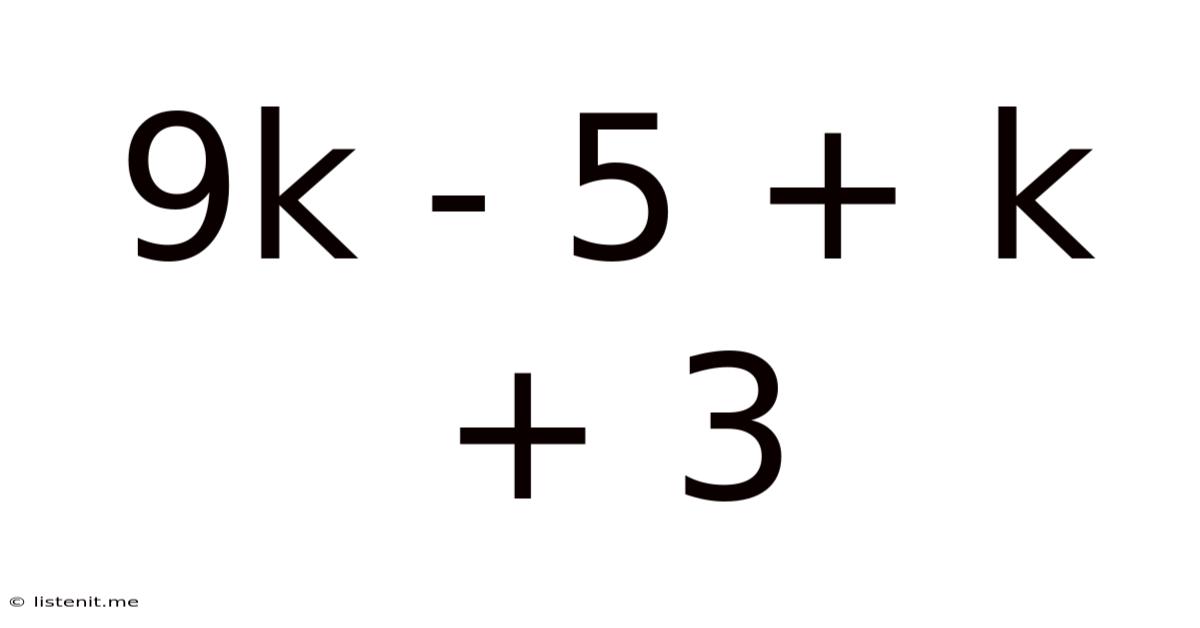
Table of Contents
Decoding the Mathematical Puzzle: 9k - 5 + k + 3
This article delves into the seemingly simple yet surprisingly rich mathematical expression: 9k - 5 + k + 3. While the equation itself might appear basic at first glance, it offers a valuable opportunity to explore fundamental algebraic concepts, problem-solving strategies, and the practical applications of simplification and manipulation in mathematics. We'll uncover its hidden depths, explore various approaches to solving it, and even touch upon its potential applications in different fields.
Understanding the Components: Variables and Constants
Before we embark on solving the equation, let's define the elements:
-
k: This represents a variable. A variable is an unknown quantity or a placeholder for a number that can change. In this equation, 'k' is the only variable. Its value is yet to be determined.
-
9, -5, and 3: These are constants. Constants are fixed numerical values that do not change. They are the unchanging parts of the equation.
Understanding the distinction between variables and constants is crucial in algebra. Constants provide fixed values, while variables allow for flexibility and the potential for various solutions depending on the value of the variable.
Simplifying the Expression: Combining Like Terms
The key to efficiently handling this equation is to combine like terms. Like terms are terms that have the same variable raised to the same power. In our equation, '9k' and 'k' are like terms because they both involve the variable 'k' raised to the power of 1 (which is usually not explicitly written).
Let's simplify:
9k - 5 + k + 3
First, combine the terms containing 'k':
9k + k = 10k
Next, combine the constant terms:
-5 + 3 = -2
Therefore, the simplified expression becomes:
10k - 2
This simplified form is equivalent to the original expression, but it's much more concise and manageable. This process of simplification is fundamental in algebra and is used extensively in more complex equations.
Solving for 'k': Finding the Value of the Variable
The simplified expression, 10k - 2, is not an equation in itself. It's an algebraic expression. To solve for 'k', we need an equation – that is, we need to set the expression equal to a specific value. Let's explore different scenarios:
Scenario 1: Setting the Expression Equal to Zero
Let's set the expression equal to zero:
10k - 2 = 0
Now, we can solve for 'k':
- Add 2 to both sides: 10k = 2
- Divide both sides by 10: k = 2/10 = 1/5 or 0.2
Therefore, if 9k - 5 + k + 3 = 0, then k = 0.2
Scenario 2: Setting the Expression Equal to a Specific Value
Let's say we want to find the value of 'k' when the expression equals 18:
10k - 2 = 18
Solving for 'k':
- Add 2 to both sides: 10k = 20
- Divide both sides by 10: k = 2
Therefore, if 9k - 5 + k + 3 = 18, then k = 2
Scenario 3: Solving for 'k' with Different Values
The beauty of algebra lies in its generality. We can substitute any numerical value for the expression and then solve for k. For instance:
If 10k - 2 = 50, then:
- 10k = 52
- k = 5.2
If 10k - 2 = -12, then:
- 10k = -10
- k = -1
Applications and Further Exploration
The seemingly simple equation 9k - 5 + k + 3 and its simplified form, 10k - 2, have broader applications in various fields:
-
Computer Programming: This type of algebraic manipulation is fundamental in programming algorithms and developing efficient code. Variables are used to represent data, and equations are used to process and manipulate that data.
-
Physics and Engineering: Equations like this form the basis of numerous physical laws and engineering calculations. Understanding how to simplify and solve these equations is vital in these fields.
-
Finance and Economics: Similar equations are used in financial modeling and economic forecasting to predict outcomes based on variable inputs.
-
Data Analysis and Statistics: Variables and equations are integral in statistical modeling, data interpretation, and making predictions based on data trends.
Advanced Concepts and Extensions
This basic equation can serve as a stepping stone to more advanced mathematical concepts:
-
Functions: The expression 10k - 2 can be defined as a function, where the input is 'k' and the output is the result of the expression. This opens the door to function notation, graphing functions, and exploring their properties.
-
Inequalities: Instead of setting the expression equal to a specific value, we could explore inequalities. For example: 10k - 2 > 0. Solving this inequality would give us the range of values for 'k' that satisfy the condition.
-
Systems of Equations: The concept can be extended to more complex systems where multiple equations with multiple variables need to be solved simultaneously.
-
Calculus: While beyond the scope of this introductory explanation, understanding the fundamental manipulation of algebraic expressions is crucial when learning calculus and its various applications.
Conclusion: The Power of Simplicity
The equation 9k - 5 + k + 3, while seemingly simple, reveals the power and elegance of algebra. It demonstrates how simplification, combining like terms, and solving for variables are fundamental processes in mathematics with vast real-world applications. By mastering these fundamental skills, one opens doors to exploring a wide range of advanced mathematical concepts and their applications across various fields. The key takeaway is that even seemingly basic equations possess significant depth and are the building blocks for more complex mathematical explorations. The ability to manipulate and solve equations like this provides a solid foundation for future mathematical endeavors.
Latest Posts
Latest Posts
-
2 3 As A Improper Fraction
May 11, 2025
-
20 Out Of 50 Is What Percent
May 11, 2025
-
Metamorphic Rock Is Changed Into Igneous Rock By
May 11, 2025
-
Calcium Forms An Ion With A Charge Of
May 11, 2025
-
How To Find An Exponential Equation From Two Points
May 11, 2025
Related Post
Thank you for visiting our website which covers about 9k - 5 + K + 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.