90 Of What Number Is 63
listenit
Apr 01, 2025 · 4 min read
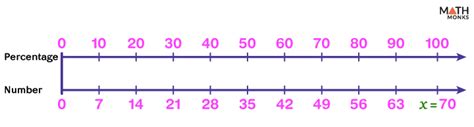
Table of Contents
90% of What Number is 63? A Comprehensive Guide to Percentage Calculations
Finding the answer to "90% of what number is 63?" involves understanding percentages and applying a simple algebraic equation. This seemingly straightforward question opens the door to exploring various percentage calculation methods, their applications in real-world scenarios, and even touches upon advanced mathematical concepts. This article will delve deep into this problem, providing multiple solutions and exploring the broader context of percentage calculations.
Understanding Percentages
Before jumping into the solution, let's solidify our understanding of percentages. A percentage is a fraction or ratio expressed as a number out of 100. The symbol % denotes percentage. For example, 50% means 50 out of 100, which is equivalent to 50/100 or 1/2 (one-half). Understanding this fundamental concept is crucial for solving percentage problems.
Method 1: Using Algebra to Solve "90% of What Number is 63?"
The question "90% of what number is 63?" can be translated into an algebraic equation. Let's represent the unknown number with the variable 'x'. The equation becomes:
0.90x = 63
To solve for 'x', we need to isolate it. We can do this by dividing both sides of the equation by 0.90:
x = 63 / 0.90
x = 70
Therefore, 90% of 70 is 63.
Method 2: Using Proportions to Solve Percentage Problems
Proportions offer another effective method for solving percentage problems. A proportion is a statement that two ratios are equal. We can set up a proportion as follows:
90/100 = 63/x
This proportion states that the ratio of 90 to 100 is equal to the ratio of 63 to the unknown number 'x'. To solve for 'x', we can cross-multiply:
90x = 6300
Now, divide both sides by 90:
x = 6300 / 90
x = 70
Again, we find that 70 is the number we're looking for.
Method 3: Working with Fractions
Percentages can also be expressed as fractions. 90% is equivalent to 90/100, which simplifies to 9/10. We can rewrite the problem as:
(9/10) * x = 63
To solve for 'x', multiply both sides by 10/9 (the reciprocal of 9/10):
x = 63 * (10/9)
x = 70
This method reinforces the equivalence between percentages, decimals, and fractions.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is essential in numerous real-world situations. Here are a few examples:
-
Finance: Calculating interest rates, discounts, taxes, and profit margins all rely heavily on percentage calculations. For example, determining the total cost of an item after a sales tax is applied involves calculating a percentage of the original price.
-
Business: Analyzing sales data, market share, and profit often involves working with percentages. Understanding percentage changes helps businesses track their performance and make informed decisions.
-
Science: Many scientific concepts utilize percentages, such as expressing concentrations of solutions or describing the probability of events. For example, a scientist might express the concentration of a substance as a percentage of the total volume.
-
Everyday Life: Calculating tips at restaurants, understanding discounts in stores, and interpreting statistics presented in news reports all involve working with percentages.
Beyond the Basics: Advanced Percentage Concepts
While the problem "90% of what number is 63?" is relatively straightforward, the underlying concepts extend to more complex scenarios. Let's explore some advanced concepts:
-
Percentage Increase/Decrease: Calculating percentage changes (increases or decreases) involves comparing two values and expressing the difference as a percentage of the original value. The formula for percentage change is: [(New Value - Old Value) / Old Value] * 100%.
-
Compound Interest: This is a crucial concept in finance where interest earned in one period is added to the principal, and subsequent interest calculations are based on the new, higher principal amount. Compound interest calculations involve repeated percentage calculations.
-
Percentage Points: It's important to distinguish between percentage change and percentage points. A change from 10% to 20% is a 10 percentage point increase, but a 100% percentage increase. This subtle difference is crucial for clear communication of data.
Tips for Solving Percentage Problems
Here are some helpful tips to make solving percentage problems easier:
-
Convert Percentages to Decimals or Fractions: This often simplifies the calculations.
-
Use Algebraic Equations or Proportions: These methods provide structured approaches to solving percentage problems.
-
Check Your Work: Always verify your answers to ensure accuracy.
Conclusion: Mastering Percentage Calculations
The seemingly simple question, "90% of what number is 63?" provides a springboard for understanding the versatility and importance of percentage calculations in various fields. From simple applications in daily life to more complex scenarios in finance and science, mastering percentage calculations is a valuable skill. By employing algebraic equations, proportions, or fractional representations, solving percentage problems becomes manageable and insightful. Remember to practice regularly to build your proficiency and confidence in tackling diverse percentage-related challenges. The more you practice, the more intuitive and effortless these calculations will become. Understanding these concepts not only improves problem-solving skills but also enhances your ability to interpret and analyze data presented in percentages across different contexts.
Latest Posts
Latest Posts
-
Is Gasoline Evaporated A Chemical Change
Apr 02, 2025
-
Find The Constant A Such That The Function Is Continuous
Apr 02, 2025
-
How Many Ounces Is 500ml Of Water
Apr 02, 2025
-
What Is The Simplest Form Of 9 12
Apr 02, 2025
-
Write Each Equation In Standard Form Using Integers
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about 90 Of What Number Is 63 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
