9 To The 3 2 Power
listenit
Apr 01, 2025 · 5 min read
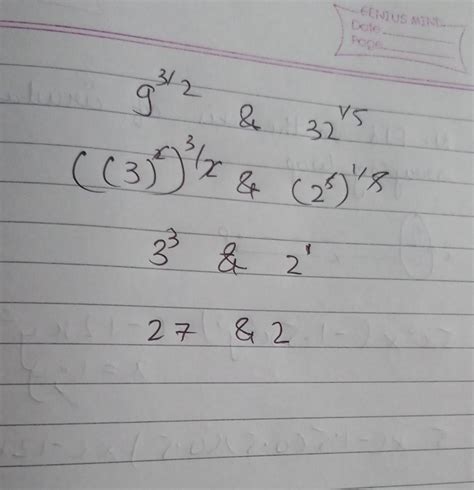
Table of Contents
- 9 To The 3 2 Power
- Table of Contents
- Decoding 9 to the Power of 32: A Deep Dive into Exponential Growth
- Understanding Exponents and Their Properties
- 1. Product of Powers: When multiplying two numbers with the same base, add the exponents: a<sup>m</sup> * a<sup>n</sup> = a<sup>(m+n)</sup>
- 2. Quotient of Powers: When dividing two numbers with the same base, subtract the exponents: a<sup>m</sup> / a<sup>n</sup> = a<sup>(m-n)</sup>
- 3. Power of a Power: When raising a power to another power, multiply the exponents: (a<sup>m</sup>)<sup>n</sup> = a<sup>(mn)</sup>*
- 4. Power of a Product: When raising a product to a power, raise each factor to that power: (ab)<sup>n</sup> = a<sup>n</sup> * b<sup>n</sup>
- 5. Power of a Quotient: When raising a quotient to a power, raise both the numerator and denominator to that power: (a/b)<sup>n</sup> = a<sup>n</sup> / b<sup>n</sup>
- Calculating 9 to the Power of 32
- Practical Applications of Exponential Growth
- 1. Finance and Compound Interest: Compound interest is a classic example of exponential growth. The interest earned each period is added to the principal, and subsequent interest is calculated on the larger amount. This snowball effect leads to exponential growth of investments over time. The longer the investment period, the more dramatic the growth.
- 2. Population Growth: Under ideal conditions, populations (of humans, bacteria, animals) often exhibit exponential growth. Each individual contributes to the overall growth, leading to a rapid increase in population size over time. Understanding exponential growth models is crucial for predicting population trends and managing resource allocation.
- 3. Computer Science and Algorithmic Complexity: Many algorithms have time or space complexities that are exponential. This means that the resources required (time or memory) grow exponentially with the input size. Efficient algorithms are crucial to mitigate the exponential growth and avoid performance bottlenecks.
- 4. Physics and Radioactive Decay: Radioactive decay is a process where unstable atomic nuclei decay at an exponential rate. The half-life of a radioactive substance describes the time it takes for half of the substance to decay. This concept is fundamental in nuclear physics, medicine, and environmental science.
- 5. Biology and Cell Division: Cellular growth in living organisms often follows exponential patterns. Cells divide, creating more cells, which in turn divide, leading to rapid growth and development of tissues and organs.
- The Significance of Large Numbers and Exponential Growth
- Beyond the Calculation: Understanding the Implications
- Latest Posts
- Latest Posts
- Related Post
Decoding 9 to the Power of 32: A Deep Dive into Exponential Growth
The expression "9 to the power of 32" (or 9<sup>32</sup>) might seem intimidating at first glance. It represents a colossal number, far beyond what we can easily grasp. However, understanding how to calculate such exponents, their implications, and the underlying mathematical principles is crucial for anyone working with advanced mathematics, computer science, or even finance. This article will delve into the intricacies of 9<sup>32</sup>, exploring its calculation, practical applications, and the broader concepts of exponential growth.
Understanding Exponents and Their Properties
Before tackling 9<sup>32</sup> directly, let's refresh our understanding of exponents. An exponent indicates how many times a base number is multiplied by itself. In the expression a<sup>n</sup>, 'a' is the base, and 'n' is the exponent. For example:
- 2<sup>3</sup> = 2 * 2 * 2 = 8
- 5<sup>2</sup> = 5 * 5 = 25
- 10<sup>4</sup> = 10 * 10 * 10 * 10 = 10,000
Several properties govern exponents, simplifying complex calculations:
1. Product of Powers: When multiplying two numbers with the same base, add the exponents: a<sup>m</sup> * a<sup>n</sup> = a<sup>(m+n)</sup>
2. Quotient of Powers: When dividing two numbers with the same base, subtract the exponents: a<sup>m</sup> / a<sup>n</sup> = a<sup>(m-n)</sup>
3. Power of a Power: When raising a power to another power, multiply the exponents: (a<sup>m</sup>)<sup>n</sup> = a<sup>(mn)</sup>*
4. Power of a Product: When raising a product to a power, raise each factor to that power: (ab)<sup>n</sup> = a<sup>n</sup> * b<sup>n</sup>
5. Power of a Quotient: When raising a quotient to a power, raise both the numerator and denominator to that power: (a/b)<sup>n</sup> = a<sup>n</sup> / b<sup>n</sup>
These properties are fundamental to efficiently handling exponential expressions, including calculating 9<sup>32</sup>.
Calculating 9 to the Power of 32
Calculating 9<sup>32</sup> directly by repeated multiplication is impractical. The number is simply too large. However, we can employ the properties of exponents and a bit of strategic thinking to simplify the calculation.
One approach is to break down the exponent into smaller, manageable parts. We can rewrite 9<sup>32</sup> as (9<sup>2</sup>)<sup>16</sup>. Since 9<sup>2</sup> = 81, the expression becomes 81<sup>16</sup>. This is still a large number, but significantly smaller than directly calculating 9 multiplied by itself 32 times.
Further simplification can be achieved by breaking down 81<sup>16</sup> into smaller powers. However, even with these simplifications, manual calculation remains cumbersome. Modern calculators and computing software are indispensable for handling such large numbers.
Using a calculator or software, we find that:
9<sup>32</sup> = 3433683820292512484657849089281
This is a 29-digit number, showcasing the rapid growth inherent in exponential functions.
Practical Applications of Exponential Growth
The concept of exponential growth, exemplified by 9<sup>32</sup>, is ubiquitous in various fields:
1. Finance and Compound Interest: Compound interest is a classic example of exponential growth. The interest earned each period is added to the principal, and subsequent interest is calculated on the larger amount. This snowball effect leads to exponential growth of investments over time. The longer the investment period, the more dramatic the growth.
2. Population Growth: Under ideal conditions, populations (of humans, bacteria, animals) often exhibit exponential growth. Each individual contributes to the overall growth, leading to a rapid increase in population size over time. Understanding exponential growth models is crucial for predicting population trends and managing resource allocation.
3. Computer Science and Algorithmic Complexity: Many algorithms have time or space complexities that are exponential. This means that the resources required (time or memory) grow exponentially with the input size. Efficient algorithms are crucial to mitigate the exponential growth and avoid performance bottlenecks.
4. Physics and Radioactive Decay: Radioactive decay is a process where unstable atomic nuclei decay at an exponential rate. The half-life of a radioactive substance describes the time it takes for half of the substance to decay. This concept is fundamental in nuclear physics, medicine, and environmental science.
5. Biology and Cell Division: Cellular growth in living organisms often follows exponential patterns. Cells divide, creating more cells, which in turn divide, leading to rapid growth and development of tissues and organs.
The Significance of Large Numbers and Exponential Growth
Numbers like 9<sup>32</sup> highlight the sheer scale of exponential growth. While we might struggle to visualize such vast quantities, understanding the underlying principles of exponential functions and their implications is essential. They govern processes across various disciplines, offering both opportunities and challenges. Managing exponential growth, whether in finance, population dynamics, or computer science, requires careful planning and strategic thinking.
Beyond the Calculation: Understanding the Implications
The calculation of 9<sup>32</sup> is important, but it's equally vital to understand the implications of such a large number and the concept of exponential growth as a whole. This number's magnitude demonstrates the power of compounding growth, highlighting the importance of early investment, efficient algorithms, and mindful resource management in situations exhibiting exponential behaviour. It serves as a potent reminder of the often-unforeseen consequences of unchecked exponential processes.
By understanding the underlying mathematical principles and their practical applications, we can better navigate and harness the potential of exponential growth, while mitigating its potential negative impacts. The journey from a seemingly simple calculation to an understanding of the broader implications showcases the power of mathematics in explaining and interpreting the world around us. It's not simply about the number itself; it's about what that number represents and the wider context of exponential growth.
Latest Posts
Latest Posts
-
What Is Smaller Than A Cell
Apr 04, 2025
-
What Is 3 4 1 2
Apr 04, 2025
-
Words With The Root Word Hyper
Apr 04, 2025
-
What Is The Electron Configuration Of K
Apr 04, 2025
-
Is Pressure And Temperature Directly Proportional
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about 9 To The 3 2 Power . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
