9 Is 1 3 Of What Number In Fraction
listenit
May 24, 2025 · 5 min read
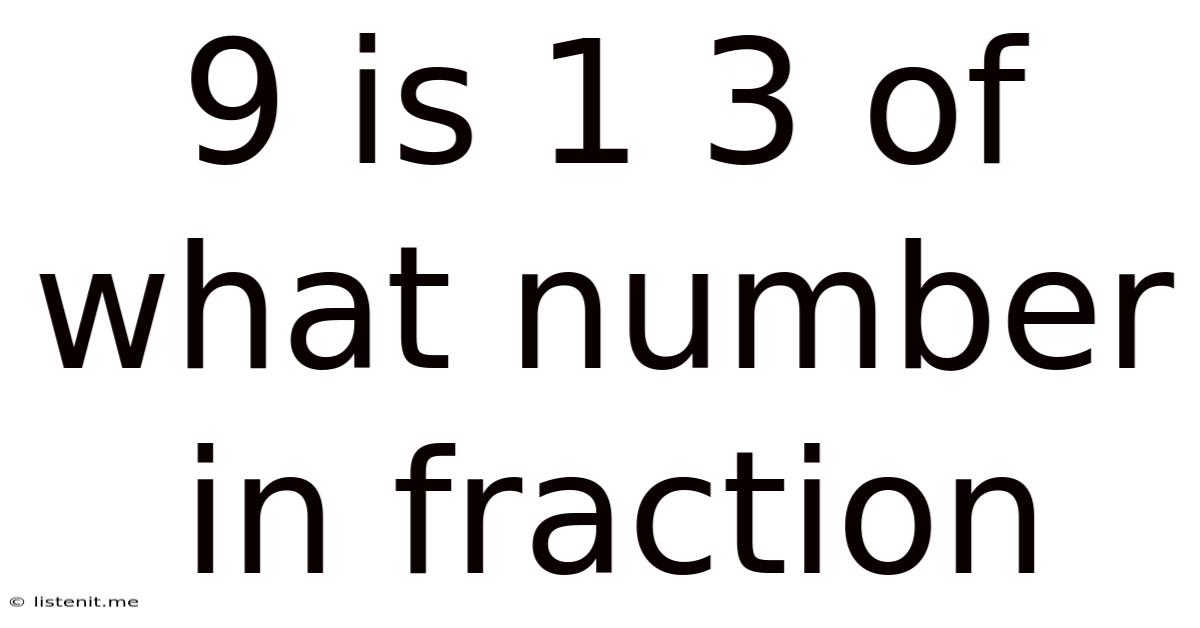
Table of Contents
9 is 1/3 of What Number? A Comprehensive Guide to Solving Fraction Problems
This article delves deep into the question, "9 is 1/3 of what number?" We'll not only solve this specific problem but also equip you with the knowledge and strategies to tackle similar fraction problems with confidence. Understanding fractions is crucial for various aspects of life, from baking to budgeting, and mastering them builds a strong foundation in mathematics.
Understanding the Problem: Deconstructing the Question
The question, "9 is 1/3 of what number?" is essentially asking us to find the whole number when we know a fraction of it. It’s a classic example of a problem involving fractions and proportions. Let's break it down:
- "9 is...": This tells us the value of a part of a larger whole.
- "...1/3 of...": This indicates the fractional part of the whole that 9 represents. 1/3 means one part out of three equal parts.
- "...what number?": This is the unknown we need to find – the total value of the whole.
Method 1: Using Algebra to Solve the Problem
Algebra offers a precise and methodical approach to solving this type of fraction problem. Let's represent the unknown number with the variable 'x'. We can translate the problem into an algebraic equation:
9 = (1/3)x
To solve for x, we need to isolate it on one side of the equation. We can do this by multiplying both sides of the equation by 3 (the reciprocal of 1/3):
3 * 9 = 3 * (1/3)x
This simplifies to:
27 = x
Therefore, 9 is 1/3 of 27.
Method 2: Using Proportions to Solve the Problem
Proportions provide another effective way to approach this problem. A proportion is a statement that two ratios are equal. We can set up a proportion using the information given:
9/x = 1/3
Here, 9 represents the part, x represents the whole, and 1/3 represents the fraction. To solve for x, we can cross-multiply:
9 * 3 = 1 * x
This simplifies to:
27 = x
Again, we find that 9 is 1/3 of 27.
Method 3: Visual Representation and Reasoning
For those who prefer a more visual approach, we can imagine dividing the whole number into three equal parts. Since 9 represents one of those parts, we can simply multiply 9 by 3 to find the total value of the whole:
9 * 3 = 27
This method relies on understanding the concept of fractions as parts of a whole.
Extending the Concepts: Solving Similar Fraction Problems
The strategies used to solve "9 is 1/3 of what number?" can be applied to a wide range of fraction problems. Let's explore some variations:
Example 1: 12 is 2/5 of what number?
Using algebra:
12 = (2/5)x Multiply both sides by 5/2 (the reciprocal of 2/5): (5/2) * 12 = (5/2) * (2/5)x 30 = x
Therefore, 12 is 2/5 of 30.
Example 2: 15 is 3/4 of what number?
Using proportions:
15/x = 3/4 Cross-multiply: 15 * 4 = 3 * x 60 = 3x Divide both sides by 3: x = 20
Therefore, 15 is 3/4 of 20.
Practical Applications of Fraction Problems
Understanding how to solve fraction problems like this isn't just about passing math tests; it's a valuable skill applicable to many real-world situations:
- Cooking and Baking: Recipes often use fractions. If a recipe calls for 1/2 cup of sugar, and you want to double the recipe, you'll need to solve a fraction problem to determine the new amount.
- Finance and Budgeting: Calculating percentages, discounts, and interest rates all involve working with fractions. Understanding how fractions work can help you make informed financial decisions.
- Measurement and Construction: Many construction projects and engineering tasks require precise measurements, which often involve fractions and decimals.
- Data Analysis: Interpreting data and statistics frequently involves working with fractions and proportions to understand trends and make inferences.
Troubleshooting Common Mistakes
When working with fractions, certain errors can occur. Here are some common mistakes to watch out for:
- Incorrectly applying reciprocals: Remember to multiply by the reciprocal when solving algebraic equations involving fractions. Multiplying by the fraction itself will not isolate the variable.
- Errors in cross-multiplication: When using proportions, ensure you multiply correctly across the equal sign.
- Misunderstanding the problem's context: Carefully read the problem statement to correctly identify the part and the whole.
Mastering Fractions: Practice Makes Perfect
The key to mastering fractions is consistent practice. Try solving various fraction problems using different methods to solidify your understanding. Start with simple problems and gradually progress to more complex ones. Online resources and workbooks can provide ample opportunities for practice.
Conclusion: Becoming a Fraction Expert
This article has explored the question, "9 is 1/3 of what number?" in depth, providing three different methods for solving this type of problem. Beyond the specific solution, we've also examined the broader principles of working with fractions, their real-world applications, and common pitfalls to avoid. By mastering these concepts, you'll not only be able to tackle similar fraction problems with confidence but also build a stronger foundation in mathematics for various applications in your life. Remember, consistent practice and a clear understanding of the underlying principles are key to success. So grab a pencil, work through some examples, and become a fraction expert!
Latest Posts
Latest Posts
-
How Many Btu To Heat 900 Sq Ft
May 24, 2025
-
Where Is The Calculator On The Ww App
May 24, 2025
-
What Is 30 Percent Of 125
May 24, 2025
-
Greatest Common Factor Of 24 And 84
May 24, 2025
-
20 Divided By 3 In Fraction
May 24, 2025
Related Post
Thank you for visiting our website which covers about 9 Is 1 3 Of What Number In Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.