9 10 Divided By 1 5
listenit
May 24, 2025 · 5 min read
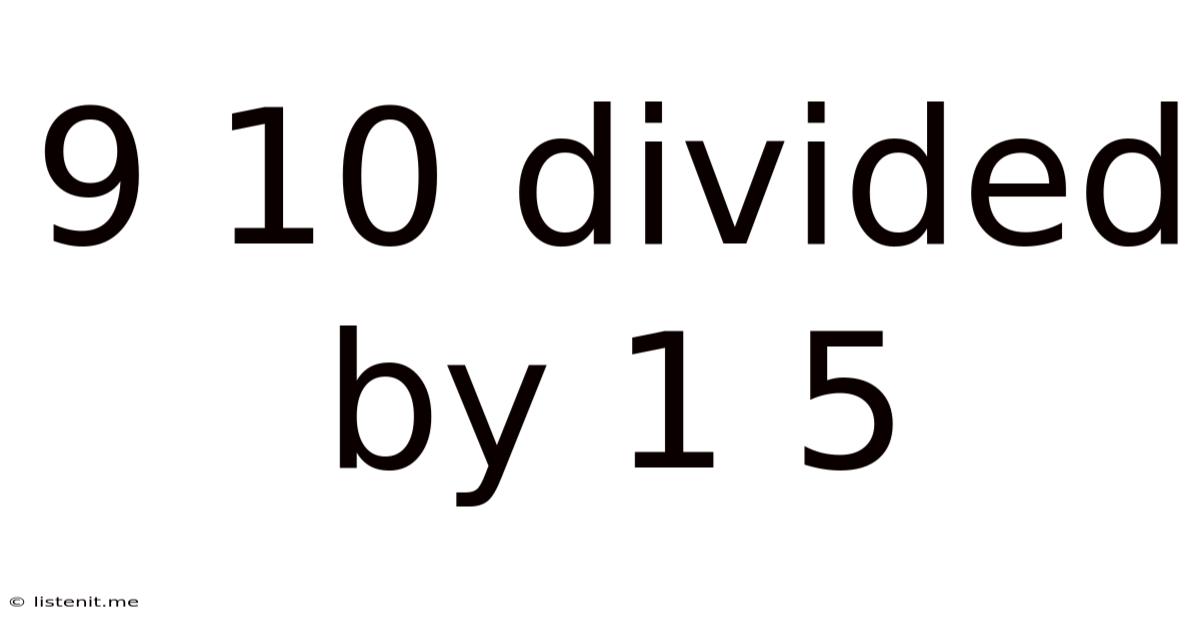
Table of Contents
9/10 Divided by 1/5: A Deep Dive into Fraction Division
This seemingly simple math problem, 9/10 divided by 1/5, offers a fantastic opportunity to explore the intricacies of fraction division, a concept crucial for a strong foundation in mathematics. While the answer itself is straightforward, understanding why the solution works is key to mastering more complex mathematical concepts later on. This article will provide a comprehensive explanation, covering various approaches and emphasizing the underlying principles.
Understanding Fraction Division
Before tackling the specific problem, let's establish a solid understanding of fraction division. The core principle lies in the concept of reciprocals (also known as multiplicative inverses). The reciprocal of a fraction is obtained by swapping its numerator and denominator. For example, the reciprocal of 2/3 is 3/2, and the reciprocal of 5 is 1/5 (since 5 can be written as 5/1).
Dividing by a fraction is equivalent to multiplying by its reciprocal. This is a fundamental rule that simplifies the process significantly. Instead of directly dividing by a fraction, we convert the division problem into a multiplication problem.
The Rule: a/b ÷ c/d = a/b * d/c
This rule holds true regardless of the specific values of a, b, c, and d (provided that b and c are not zero, as division by zero is undefined).
Solving 9/10 Divided by 1/5
Now, let's apply this principle to our problem: 9/10 ÷ 1/5.
Following the rule above, we rewrite the division as multiplication:
9/10 ÷ 1/5 = 9/10 * 5/1
Now we simply multiply the numerators together and the denominators together:
(9 * 5) / (10 * 1) = 45/10
This fraction can be simplified by finding the greatest common divisor (GCD) of the numerator and denominator. The GCD of 45 and 10 is 5. Dividing both the numerator and the denominator by 5, we get:
45/10 = 9/2
Finally, we can convert this improper fraction to a mixed number:
9/2 = 4 ½
Therefore, the solution to 9/10 divided by 1/5 is 4 ½ or 4.5.
Alternative Approaches and Visual Representations
While the reciprocal method is the most efficient, understanding the problem from different perspectives can solidify your comprehension.
Visual Representation using Area Models
Imagine a rectangle representing one whole unit. Divide this rectangle into 10 equal parts, representing 1/10 each. Now shade 9 of these parts to represent 9/10. Dividing by 1/5 means finding out how many 1/5 units are contained within the shaded 9/10. You'll find that four and a half 1/5 units fit within the 9/10 area.
Repeated Subtraction
Though less efficient for this problem, the concept of repeated subtraction can help visualize fraction division. How many times can we subtract 1/5 from 9/10? This approach would involve finding a common denominator (which would be 10), rewriting 1/5 as 2/10 and then repeatedly subtracting 2/10 from 9/10. This method, while valid, is more cumbersome than using reciprocals.
Expanding on Fraction Division: Real-World Applications
Understanding fraction division isn't just about solving textbook problems; it has significant real-world applications across various fields:
-
Cooking and Baking: Scaling recipes up or down requires dividing and multiplying fractions. For example, if a recipe calls for 1/2 cup of flour and you want to make half the recipe, you'd need to divide 1/2 by 2.
-
Sewing and Crafts: Working with fabric or other materials often requires precise measurements involving fractions. Cutting a piece of fabric into smaller sections involves fraction division.
-
Construction and Engineering: Precise measurements and calculations are crucial in these fields, requiring a strong understanding of fraction division. For example, dividing a length of pipe into smaller segments.
-
Data Analysis and Statistics: Many statistical calculations involve fractions and their manipulation, including division.
-
Financial Calculations: Dividing shares, calculating proportions of investments, and many other financial operations involve fractions and their division.
Mastering Fractions: Tips and Practice
Proficiency in fraction division, and fractions in general, requires consistent practice and a focused understanding of the underlying principles. Here are a few tips:
-
Master the basics: Ensure you have a solid understanding of simplifying fractions, finding common denominators, and converting between improper and mixed fractions.
-
Practice regularly: Consistent practice is key to building proficiency. Work through various problems, starting with simpler ones and gradually increasing the difficulty.
-
Visual aids: Use diagrams, area models, or other visual aids to help visualize the concept of fraction division. This can be particularly helpful for beginners.
-
Seek help when needed: Don't hesitate to ask for help from teachers, tutors, or online resources if you're struggling with a particular concept.
-
Real-world application: Try to find and apply fraction division in real-world scenarios. This will not only reinforce the concepts but also demonstrate their practical relevance.
Beyond the Basics: Exploring More Complex Fraction Problems
The problem 9/10 divided by 1/5 serves as a springboard to understanding more intricate fraction calculations. Once you master this foundational concept, you can progress to tackling more complex problems involving mixed numbers, decimals, and combinations of operations.
Remember, the key to success lies in understanding the core principles, practicing regularly, and approaching problems systematically. With consistent effort and a focused approach, mastering fraction division, and more advanced mathematical concepts, will become attainable.
Conclusion
While the answer to 9/10 divided by 1/5 is a simple 4 ½, the journey of understanding the how and why behind this solution provides a valuable stepping stone in developing stronger mathematical skills. By employing the reciprocal method, visualizing the process, and understanding its real-world applications, we can appreciate the significance of fraction division and its role in numerous aspects of our daily lives. Continue practicing, exploring different approaches, and embrace the challenges – your mathematical journey awaits!
Latest Posts
Latest Posts
-
125 Out Of 200 As A Percentage
May 24, 2025
-
Born In 1982 How Old In 2023
May 24, 2025
-
What Is The Greatest Common Factor Of 45 And 72
May 24, 2025
-
5 Billion Divided By 250 Million
May 24, 2025
-
83 As A Fraction Of An Inch
May 24, 2025
Related Post
Thank you for visiting our website which covers about 9 10 Divided By 1 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.