80 Percent Of What Number Is 20
listenit
May 12, 2025 · 5 min read
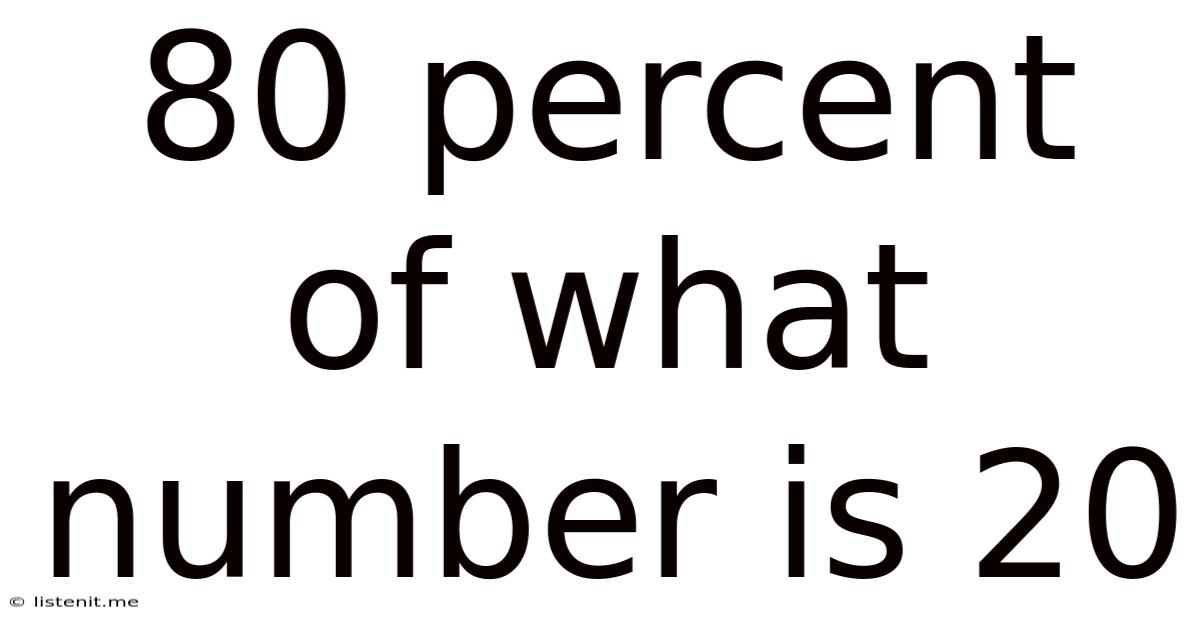
Table of Contents
80 Percent of What Number is 20? Unraveling the Math and its Applications
Finding the answer to "80 percent of what number is 20?" might seem like a simple math problem, but it unlocks a powerful understanding of percentages and their real-world applications. This article will not only provide the solution but also delve into the underlying mathematical concepts, explore different methods for solving similar problems, and showcase how this type of calculation is used across various fields. We'll cover everything from basic percentage calculations to practical examples and even touch upon advanced percentage-related concepts.
Understanding Percentages: The Foundation
Before diving into the solution, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a part of 100. For instance, 80% can be written as 80/100, which simplifies to 4/5 or 0.8 as a decimal. This means 80% represents 80 parts out of a total of 100 parts. Understanding this fundamental concept is crucial for tackling percentage problems.
Key Percentage Concepts:
- Percentage: A ratio or fraction expressed as a part of 100.
- Base: The whole amount or the original number (the number we are finding a percentage of).
- Rate: The percentage itself (in our problem, 80%).
- Portion: The part of the base represented by the percentage (in our problem, 20).
Solving "80 Percent of What Number is 20?"
Now, let's tackle the core problem: 80% of what number is 20? We can solve this using several methods:
Method 1: Using the Equation
The most straightforward method involves setting up an equation. Let's represent the unknown number as 'x'. We can then write the equation as:
0.8 * x = 20
To solve for x, we divide both sides of the equation by 0.8:
x = 20 / 0.8
x = 25
Therefore, 80% of 25 is 20.
Method 2: Using Proportions
Proportions offer another elegant way to solve this type of problem. We can set up a proportion as follows:
80/100 = 20/x
Cross-multiplying, we get:
80 * x = 20 * 100
80x = 2000
Dividing both sides by 80:
x = 2000 / 80
x = 25
Again, we find that the unknown number is 25.
Method 3: Working Backwards from the Percentage
Since 80% represents 20, we can find the value of 1% by dividing 20 by 80:
20 / 80 = 0.25
This means 1% of the unknown number is 0.25. To find the entire number (100%), we multiply 0.25 by 100:
0.25 * 100 = 25
Thus, the number is 25.
Real-World Applications of Percentage Calculations
The ability to solve percentage problems, like the one we just explored, is incredibly useful in various real-life situations. Here are some examples:
1. Business and Finance:
- Discounts and Sales: Retailers frequently offer discounts expressed as percentages. Calculating the original price before a discount is applied is crucial for both businesses and consumers. For example, if a jacket is on sale for $60 at 20% off, finding the original price requires the same type of percentage calculation.
- Profit Margins: Businesses use percentage calculations to determine their profit margins. Knowing the percentage of profit relative to the cost of goods sold is vital for financial planning.
- Interest Rates: Understanding compound interest and simple interest calculations, both heavily reliant on percentages, is fundamental to managing personal finances and investments.
- Taxes: Sales tax, income tax, and other taxes are all expressed as percentages, necessitating a clear understanding of percentage calculations for accurate financial planning.
2. Science and Statistics:
- Data Analysis: Percentages are extensively used in statistical analysis to represent proportions, trends, and relationships within data sets. For instance, analyzing survey results often involves expressing responses as percentages of the total number of respondents.
- Experimental Results: In scientific research, percentage calculations are critical for expressing and comparing experimental results. For example, measuring the success rate of an experiment, expressing it as a percentage, is a key method for reporting findings.
3. Everyday Life:
- Tip Calculations: Calculating a tip in a restaurant typically involves finding a percentage of the total bill amount.
- Shopping: Comparing prices and determining the best deals often requires calculating percentages to compare discounts and savings.
- Recipes: Scaling recipes up or down involves adjusting ingredient quantities, often based on percentage calculations.
Advanced Percentage Concepts and Related Problems
While our initial problem was relatively straightforward, let's explore some more advanced percentage-related concepts and problem types:
1. Percentage Increase and Decrease:
Calculating percentage increases and decreases is crucial for understanding growth rates and changes over time. For instance, if a stock price increases from $50 to $60, the percentage increase is calculated as follows:
Percentage Increase = [(New Value - Old Value) / Old Value] * 100
Percentage Increase = [(60 - 50) / 50] * 100 = 20%
Similarly, percentage decrease is calculated using the same formula with a negative result indicating a decrease.
2. Compounding Percentages:
Compounding percentages occur when a percentage change is applied repeatedly to an initial value. Understanding compounding is crucial for understanding financial growth, such as with compound interest. The formula for compound growth is:
Future Value = Present Value * (1 + r)^n
Where:
- r = the interest rate (as a decimal)
- n = the number of compounding periods
3. Solving for the Rate or the Base:
While our problem focused on solving for the base, similar problems might involve solving for the rate or the portion. For example, "20 is what percent of 25?" requires solving for the rate, while "What is 80% of 25?" involves finding the portion. The same equation-based, proportion-based, or working-backwards methods can be adapted to solve these different types of percentage problems.
Conclusion: Mastering Percentages for a Data-Driven World
The seemingly simple question, "80 percent of what number is 20?" opens up a vast landscape of mathematical concepts and real-world applications. Mastering percentage calculations is not merely an academic exercise but a crucial skill for navigating the complexities of modern life, whether in business, finance, science, or everyday decision-making. By understanding the underlying principles, various solution methods, and advanced concepts, you equip yourself with a valuable toolset for analyzing data, making informed decisions, and effectively communicating quantitative information. The ability to confidently handle percentages is an invaluable asset in our increasingly data-driven world.
Latest Posts
Latest Posts
-
Which Phase Of Mitosis Takes The Longest
May 12, 2025
-
How To Find The Distance Between 2 Planes
May 12, 2025
-
Name The Smallest Angle Of Abc
May 12, 2025
-
Enzymes Decrease The Activation Energy Of A Reaction By
May 12, 2025
-
Are Critical Points And Inflection Points The Same
May 12, 2025
Related Post
Thank you for visiting our website which covers about 80 Percent Of What Number Is 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.