80 Of C Is 20 What Is C
listenit
May 10, 2025 · 4 min read
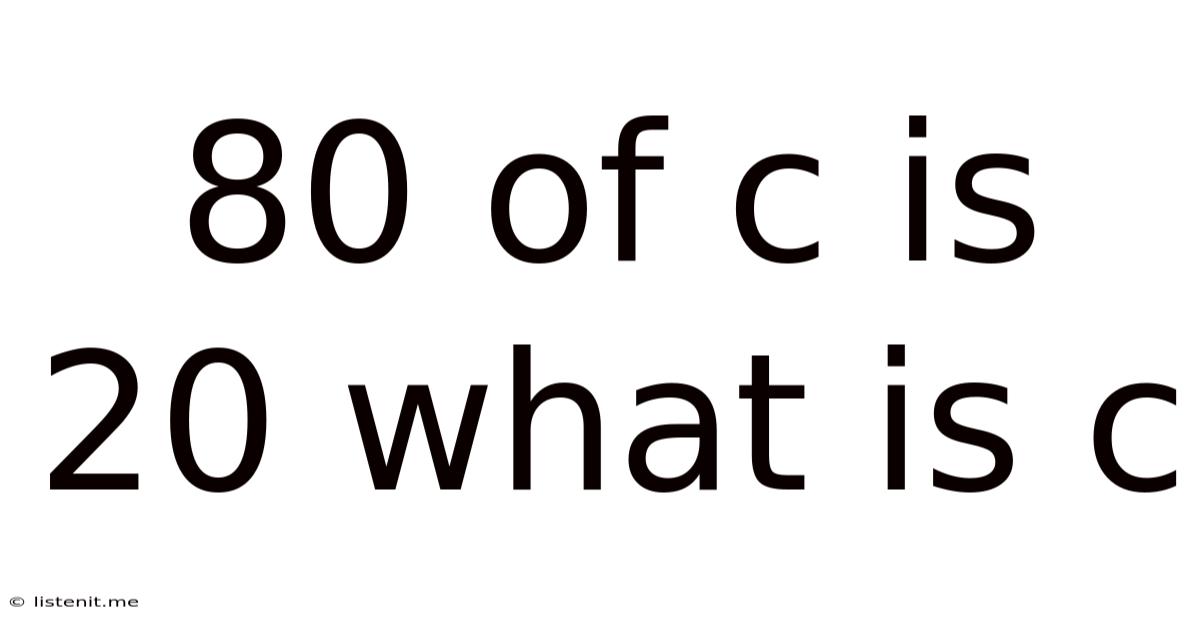
Table of Contents
80% of c is 20: What is c? Solving Percentage Problems
This article will delve into the straightforward yet fundamental concept of solving percentage problems, specifically focusing on the equation: "80% of c is 20. What is c?" We will explore multiple methods to solve this, catering to various levels of mathematical understanding. We'll also discuss the broader application of percentage calculations in various real-world scenarios. Finally, we'll touch upon related problems and how to approach them effectively.
Understanding the Problem: 80% of c = 20
The core of this problem lies in understanding the relationship between percentages, fractions, and decimals. The statement "80% of c is 20" can be translated into a mathematical equation:
0.80 * c = 20
This equation states that 80% (expressed as a decimal, 0.80) of an unknown value 'c' equals 20. Our task is to find the value of 'c'.
Method 1: Using Algebra to Solve for 'c'
The most direct method involves solving the algebraic equation:
0.80 * c = 20
To isolate 'c', we divide both sides of the equation by 0.80:
c = 20 / 0.80
c = 25
Therefore, c = 25.
Method 2: Converting Percentage to Fraction
Another approach involves converting the percentage to a fraction:
80% can be written as 80/100, which simplifies to 4/5. So the equation becomes:
(4/5) * c = 20
To solve for 'c', we multiply both sides by the reciprocal of 4/5, which is 5/4:
c = 20 * (5/4)
c = 100/4
c = 25
Again, we find that c = 25.
Method 3: Using Proportions
We can also use proportions to solve this problem. We can set up a proportion as follows:
80/100 = 20/c
This proportion states that the ratio of 80 to 100 is equal to the ratio of 20 to c. To solve for c, we cross-multiply:
80 * c = 20 * 100
80c = 2000
c = 2000 / 80
c = 25
Once again, we arrive at the solution: c = 25.
Real-World Applications of Percentage Calculations
Percentage calculations are ubiquitous in daily life. Here are a few examples:
-
Sales and Discounts: Retailers frequently offer discounts expressed as percentages. Understanding percentage calculations allows you to quickly determine the final price after a discount. For example, a 20% discount on a $100 item means you save $20 and pay $80.
-
Taxes: Sales tax, income tax, and other taxes are usually expressed as percentages. Knowing how to calculate percentages helps you understand the tax burden on purchases or income.
-
Interest Rates: Interest rates on loans, savings accounts, and investments are expressed as percentages. Understanding percentage calculations is crucial for making informed financial decisions.
-
Tips and Gratuities: When dining out or receiving services, tipping is often expressed as a percentage of the total bill.
-
Statistical Analysis: Percentages are widely used in data analysis and statistics to represent proportions and trends.
Solving Similar Percentage Problems
The core principles used to solve "80% of c is 20" can be applied to similar problems. Let's consider some variations:
Example 1: 30% of x is 15. What is x?
Using the same algebraic method:
0.30 * x = 15
x = 15 / 0.30
x = 50
Example 2: What is 25% of 60?
This time, we know the percentage and the whole number (60), and need to find the part:
0.25 * 60 = 15
Example 3: If 15 is 75% of a number, what is the number?
Let the number be y. Then:
0.75 * y = 15
y = 15 / 0.75
y = 20
Tips for Solving Percentage Problems
-
Convert Percentages to Decimals or Fractions: This simplifies calculations considerably.
-
Use Algebraic Equations: Setting up and solving algebraic equations is a systematic approach to solve percentage problems.
-
Check Your Answers: Always verify your answer by plugging it back into the original equation or statement.
-
Practice Regularly: The more you practice solving percentage problems, the more confident and efficient you will become.
Conclusion: Mastering Percentage Calculations
Understanding and mastering percentage calculations is a crucial skill with far-reaching applications in various aspects of life. This article has provided a comprehensive guide to solving percentage problems, emphasizing multiple methods and illustrating real-world applications. By employing the techniques discussed here, you can confidently tackle diverse percentage-related challenges and improve your mathematical proficiency. Remember to practice regularly and utilize the different methods to solidify your understanding and find the approach that best suits your learning style. This will not only boost your mathematical abilities but also enhance your ability to solve problems in various real-world contexts where percentage calculations play a significant role.
Latest Posts
Latest Posts
-
Which Plant Organelle Is Responsible For Photosynthesis
May 10, 2025
-
What Is The Largest Reservoir Of Nitrogen On Earth
May 10, 2025
-
Multicellular Organisms Can Be Organized Into What Levels
May 10, 2025
-
How Many Different Combinations Of 6 Numbers
May 10, 2025
-
How Many Molecules Of Nadh Are Produced During Glycolysis
May 10, 2025
Related Post
Thank you for visiting our website which covers about 80 Of C Is 20 What Is C . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.