80 Is 125 Of What Number
listenit
May 12, 2025 · 4 min read
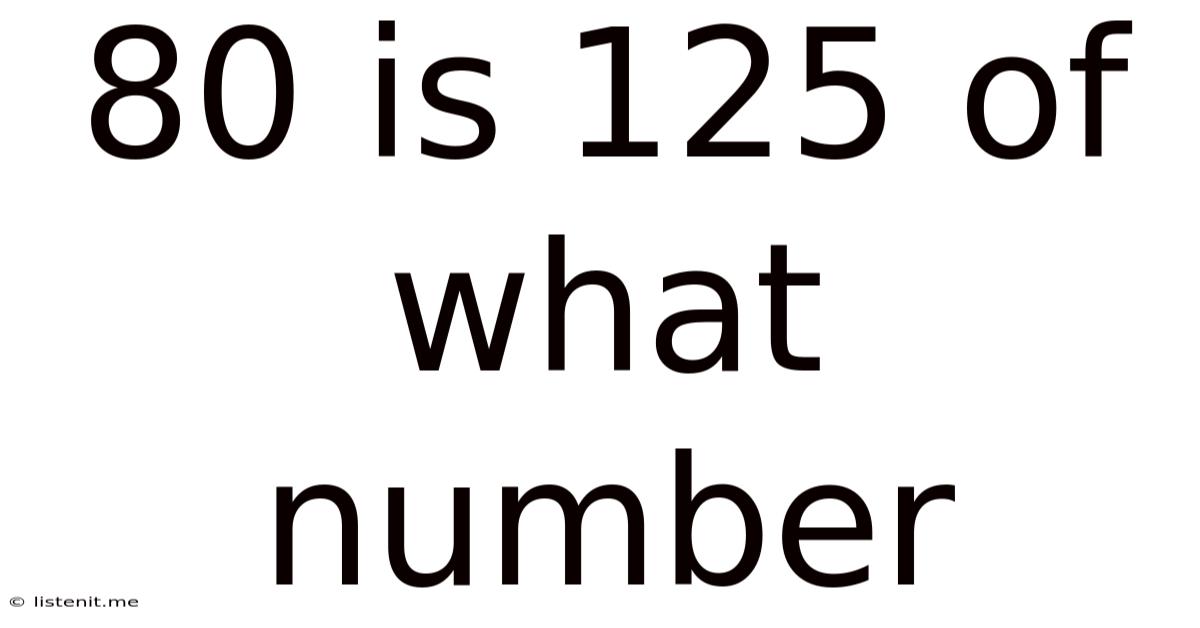
Table of Contents
80 is 125% of What Number? A Comprehensive Guide to Percentage Calculations
Understanding percentages is a fundamental skill applicable across various aspects of life, from calculating discounts and interest rates to analyzing data and interpreting statistics. This article delves into the question, "80 is 125% of what number?", providing a step-by-step solution, exploring different approaches, and expanding on the broader concept of percentage calculations. We'll also touch upon practical applications and offer tips for mastering percentage problems.
Understanding the Problem: Deconstructing "80 is 125% of What Number?"
The question "80 is 125% of what number?" presents a classic percentage problem. We're given a percentage (125%) and the resulting value (80), and our task is to find the original number. This requires understanding the relationship between percentages, parts, and the whole. Let's break it down:
- 125%: This represents a value greater than 100%, indicating that 80 is more than the original number. This means we're dealing with an increase or a value exceeding the original.
- 80: This is the result after increasing the original number by 125%.
- What number? This is the unknown variable we need to solve for. We can represent it with 'x'.
Method 1: Using the Equation Method
This is the most straightforward approach. We can translate the problem into an algebraic equation:
80 = 1.25x
Where:
- 80 is the resulting value.
- 1.25 is the decimal equivalent of 125% (125/100 = 1.25).
- x is the unknown number we're trying to find.
To solve for x, we simply divide both sides of the equation by 1.25:
x = 80 / 1.25
x = 64
Therefore, 80 is 125% of 64.
Method 2: Using Proportions
Another effective method is using proportions. We can set up a proportion to represent the relationship between the percentage and the values:
125/100 = 80/x
This proportion states that 125 is to 100 as 80 is to x. To solve for x, we cross-multiply:
125x = 80 * 100
125x = 8000
Now, divide both sides by 125:
x = 8000 / 125
x = 64
Again, we arrive at the same answer: 64.
Method 3: Working with Percentages Directly
This method focuses on understanding the relationship between the percentage increase and the original value. Since 80 represents a 125% increase, it means 80 is equal to the original number plus 25% of the original number.
Let's represent the original number as 'x'. Then:
x + 0.25x = 80
Combining like terms:
1.25x = 80
This equation is identical to the one we derived in Method 1, leading to the same solution:
x = 64
Practical Applications: Real-World Scenarios
Understanding percentage calculations is crucial for various real-world scenarios:
Finance:
- Calculating interest: Determining the principal amount based on accrued interest.
- Analyzing investment returns: Understanding the growth of investments over time.
- Calculating discounts: Determining the original price of an item after a percentage discount has been applied.
- Assessing loan repayments: Understanding how much of each payment goes towards principal and interest.
Business:
- Profit margin analysis: Calculating the percentage of profit relative to revenue.
- Sales growth tracking: Measuring the increase or decrease in sales over time.
- Market share analysis: Determining the percentage of a market held by a specific company or product.
- Inventory management: Calculating stock levels as percentages of total capacity.
Everyday Life:
- Calculating tips: Determining the appropriate tip amount in a restaurant.
- Understanding sales tax: Calculating the final price of an item including sales tax.
- Comparing prices: Determining the better value between items with different prices and discounts.
- Recipe scaling: Adjusting recipe quantities based on the number of servings.
Mastering Percentage Problems: Tips and Tricks
- Convert percentages to decimals: This simplifies calculations significantly. Remember that to convert a percentage to a decimal, divide by 100. (e.g., 125% = 1.25)
- Use algebraic equations: These provide a structured approach to solving complex percentage problems.
- Practice regularly: The more you practice, the more comfortable and efficient you'll become at solving percentage problems.
- Understand the underlying concepts: A strong understanding of the relationship between percentages, parts, and wholes is essential.
- Check your work: Always double-check your calculations to ensure accuracy. Using a calculator can help reduce errors.
- Break down complex problems: Sometimes, large percentage problems can be broken down into smaller, more manageable steps.
Expanding on Percentage Concepts
This article primarily focused on solving the specific problem "80 is 125% of what number?". However, the principles explored here can be applied to a wide range of percentage-related problems, including calculating percentage increases and decreases, determining percentage changes, and solving problems involving compound interest. Mastering these fundamental concepts is a cornerstone of numerical literacy and problem-solving.
Conclusion
Solving percentage problems, like "80 is 125% of what number?", may seem daunting at first, but by understanding the underlying concepts and applying the methods outlined in this article, you can confidently tackle such calculations. Whether you're navigating financial matters, analyzing data, or simply tackling everyday tasks, a strong grasp of percentages will greatly enhance your skills and abilities. Remember to practice regularly and apply these techniques to real-world scenarios to truly solidify your understanding.
Latest Posts
Latest Posts
-
Write The Equation For The Following Graph
May 12, 2025
-
What Is The Monomer Of Polysaccharides
May 12, 2025
-
Bond Enthalpy Vs Enthalpy Of Formation
May 12, 2025
-
How Many Valence Electrons In Kr
May 12, 2025
-
How Many Possible Combinations Of 3 Numbers 1 3
May 12, 2025
Related Post
Thank you for visiting our website which covers about 80 Is 125 Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.