8 Out Of 15 Is What Percentage
listenit
May 25, 2025 · 5 min read
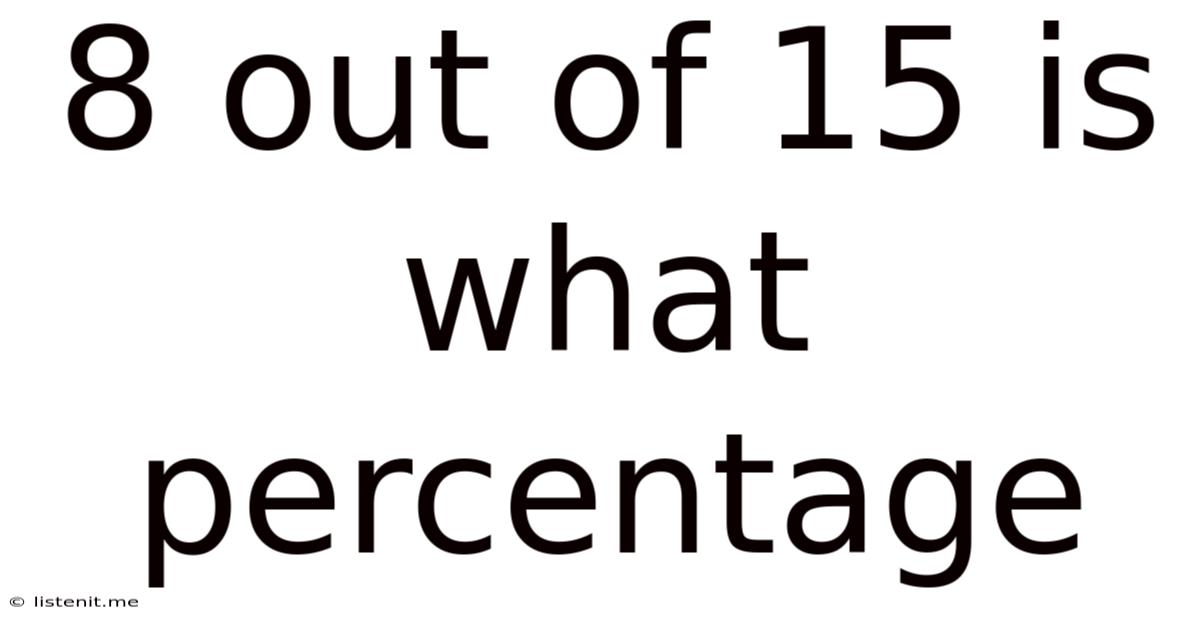
Table of Contents
8 out of 15 is what percentage? A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill with widespread applications in various aspects of life, from academic pursuits to professional settings and everyday situations. Understanding how to determine percentages is crucial for interpreting data, making informed decisions, and effectively communicating quantitative information. This comprehensive guide delves into the calculation of "8 out of 15 is what percentage?", exploring various methods, practical examples, and advanced applications to solidify your understanding of percentage calculations.
Understanding Percentages
A percentage is a fraction or ratio expressed as a number out of 100. It represents a portion of a whole. The symbol "%" denotes percentage. For instance, 50% signifies 50 out of 100, or half. Understanding this basic concept is paramount before tackling more complex percentage problems.
Calculating "8 out of 15 is what percentage?"
The core of this problem lies in translating the phrase "8 out of 15" into a percentage. We can achieve this using several methods:
Method 1: Using the Fraction Method
The most straightforward approach is to convert the ratio "8 out of 15" into a fraction and then convert that fraction into a percentage.
-
Represent as a Fraction: The phrase "8 out of 15" translates directly to the fraction 8/15.
-
Convert to Decimal: To transform this fraction into a percentage, we need a decimal representation. Divide the numerator (8) by the denominator (15): 8 ÷ 15 ≈ 0.5333
-
Convert to Percentage: Multiply the decimal by 100 to express it as a percentage: 0.5333 x 100 = 53.33%
Therefore, 8 out of 15 is approximately 53.33%.
Method 2: Using the Proportion Method
This method uses proportions to solve for the unknown percentage.
-
Set up a Proportion: We can set up a proportion where 'x' represents the unknown percentage:
8/15 = x/100
-
Cross-Multiply: Cross-multiply to solve for 'x':
15x = 800
-
Solve for x: Divide both sides by 15:
x = 800/15 ≈ 53.33
-
Express as Percentage: x ≈ 53.33%
This method confirms that 8 out of 15 is approximately 53.33%.
Method 3: Using a Calculator
Most calculators have a percentage function. Simply divide 8 by 15 and then multiply the result by 100. This provides the same answer: approximately 53.33%.
Practical Applications and Real-World Examples
Understanding percentage calculations has numerous practical applications:
-
Academic Performance: If you answered 8 questions correctly out of 15 on a test, your score is approximately 53.33%.
-
Sales and Discounts: If a store offers a 53.33% discount on an item, it means the price reduction is equivalent to paying for 8 out of every 15 items.
-
Financial Investments: Percentage calculations are crucial for monitoring investment returns and understanding growth or losses. An investment that grows by 53.33% demonstrates substantial returns.
-
Statistical Analysis: Percentages are fundamental in data analysis to visualize and interpret proportions within datasets. 53.33% could represent a substantial proportion of respondents in a survey.
-
Sports Statistics: In baseball, a batting average of .533 (which can be expressed as 53.3%) shows a high success rate of getting hits.
-
Surveys and Polls: Percentages allow you to represent the proportion of people who agree or disagree with certain statements effectively in a survey or opinion poll.
Beyond the Basics: Advanced Percentage Calculations
While calculating "8 out of 15 is what percentage?" provides a basic understanding, the application of percentages extends far beyond this simple calculation. Let's explore some advanced scenarios:
Calculating Percentage Increase or Decrease
Often, we need to determine the percentage change between two values.
Example: If a product initially cost $10 and its price increased to $15, what is the percentage increase?
-
Find the difference: $15 - $10 = $5
-
Divide the difference by the original value: $5 / $10 = 0.5
-
Multiply by 100: 0.5 x 100 = 50%
The price increased by 50%.
Finding the Original Value After a Percentage Change
Sometimes, we know the final value and the percentage change and need to find the original value.
Example: A product is currently priced at $15 after a 50% increase. What was the original price?
-
Convert the percentage to a decimal: 50% = 0.5
-
Add 1 to the decimal (because it's an increase): 1 + 0.5 = 1.5
-
Divide the final price by the result: $15 / 1.5 = $10
The original price was $10.
Calculating Percentage of a Percentage
This involves finding the percentage of a percentage.
Example: A store offers a 20% discount on an item already reduced by 10%. What is the overall discount?
-
Calculate the initial discount: 10% of the original price
-
Calculate the second discount: 20% of the remaining price (after the initial discount)
-
Sum the discounts: This gives you the overall discount. This is not simply adding 20% and 10%; instead, you need to calculate the percentages sequentially.
Troubleshooting Common Percentage Calculation Errors
Several common mistakes can occur when calculating percentages:
-
Incorrect Order of Operations: Remember to follow the order of operations (PEMDAS/BODMAS).
-
Using Incorrect Formulae: Ensure you're using the correct formula for the specific percentage calculation you are performing.
-
Rounding Errors: Rounding numbers too early can lead to significant inaccuracies in the final result.
-
Misinterpreting the Problem: Carefully read and understand the problem statement before attempting to calculate the answer.
Conclusion: Mastering Percentage Calculations
Calculating percentages is a vital skill with broad applications in many areas of life. This guide demonstrates how to calculate "8 out of 15 is what percentage?" using different methods and showcases its practical implications. Understanding the different methods and potential errors ensures accuracy and efficiency in tackling percentage problems. By mastering these techniques, you will be well-equipped to handle various percentage calculations confidently and accurately. Remember, practice is key to mastering these concepts. Work through different examples and scenarios to reinforce your understanding and build confidence in your ability to solve any percentage problem you encounter.
Latest Posts
Latest Posts
-
What Is The Gcf Of 45 And 15
May 25, 2025
-
7 Divided By 8 In Fraction Form
May 25, 2025
-
If I Weigh 250 Pounds How Many Calories
May 25, 2025
-
How Many Years From 1976 To 2024
May 25, 2025
-
How Many Years Is 1949 To 2023
May 25, 2025
Related Post
Thank you for visiting our website which covers about 8 Out Of 15 Is What Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.