8 Is What Percent Of 11
listenit
May 24, 2025 · 4 min read
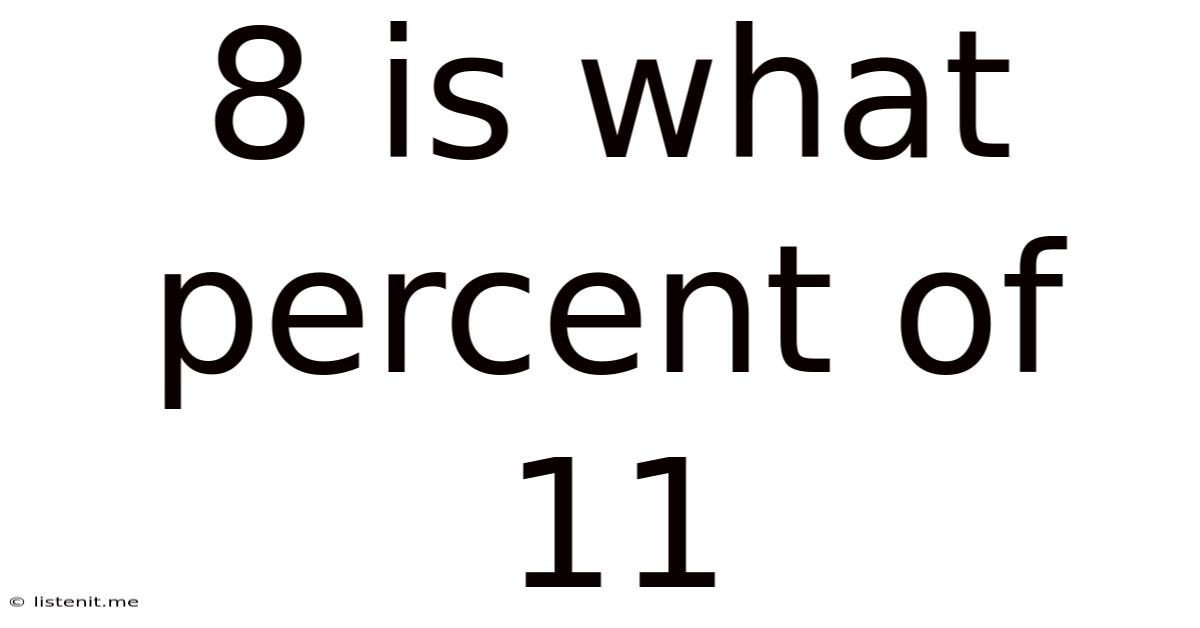
Table of Contents
8 is What Percent of 11? A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill with wide-ranging applications in various aspects of life, from everyday budgeting and shopping to more complex fields like finance and statistics. Understanding how to determine what percentage one number represents of another is crucial for making informed decisions and interpreting data effectively. This comprehensive guide will delve into the calculation of "8 is what percent of 11," offering multiple approaches and exploring the underlying concepts. We'll also examine practical applications and explore related percentage problems.
Understanding Percentages
Before diving into the specific calculation, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a number out of 100. The symbol "%" signifies "per hundred" or "out of 100." For instance, 50% means 50 out of 100, which is equivalent to the fraction ½ or the decimal 0.5.
Percentages are used to represent proportions or ratios. They allow us to easily compare different quantities and express them in a standardized format. This makes it much simpler to understand and interpret data than using fractions or decimals alone.
Method 1: Using the Formula
The most direct way to determine what percentage 8 represents of 11 is to use the standard percentage formula:
(Part / Whole) * 100% = Percentage
In this case:
- Part: 8 (the number we want to express as a percentage)
- Whole: 11 (the total number)
Substituting these values into the formula, we get:
(8 / 11) * 100% = 72.7272...%
Rounding to two decimal places, we find that 8 is approximately 72.73% of 11.
Method 2: Setting up a Proportion
Another effective method involves setting up a proportion. We can express the problem as a ratio:
8/11 = x/100
Where 'x' represents the unknown percentage. To solve for 'x', we cross-multiply:
11x = 800
x = 800/11
x ≈ 72.73
Therefore, using this proportional method, we again arrive at the answer: 8 is approximately 72.73% of 11.
Method 3: Using a Calculator
Modern calculators simplify percentage calculations considerably. Most calculators have a percentage function (%) that automates the process. Simply input "8 ÷ 11 × 100 =" to obtain the result directly. This method provides a quick and convenient way to arrive at the answer, especially when dealing with more complex percentage calculations.
Practical Applications
Understanding percentage calculations, as exemplified by this problem, has numerous real-world applications:
1. Finance and Budgeting:
- Calculating discounts: If an item is discounted by a certain percentage, knowing how to calculate the actual discount amount is essential for budgeting effectively.
- Interest rates: Understanding interest rates on loans, savings accounts, and investments relies heavily on percentage calculations.
- Tax calculations: Calculating sales tax, income tax, and other taxes often involves using percentages.
2. Statistics and Data Analysis:
- Representing proportions: Percentages are widely used to represent proportions in surveys, polls, and statistical analyses.
- Expressing changes over time: Percentages are used to express changes in variables over time, like population growth, economic indicators, or sales figures.
3. Everyday Life:
- Calculating tips: Determining the appropriate tip amount at a restaurant involves calculating a percentage of the bill.
- Understanding sales and promotions: Interpreting sales and promotional offers often requires calculating percentages to determine the actual savings.
- Comparing prices: Percentages can be helpful when comparing the prices of similar items from different stores or brands.
Related Percentage Problems
Let's explore some related problems to further enhance your understanding of percentage calculations:
Problem 1: What is 11% of 8?
This problem reverses the original scenario. We use the formula:
(Percentage/100) * Whole = Part
(11/100) * 8 = 0.88
Therefore, 11% of 8 is 0.88.
Problem 2: 15 is what percent of 25?
Using the formula:
(Part/Whole) * 100% = Percentage
(15/25) * 100% = 60%
Therefore, 15 is 60% of 25.
Problem 3: 20% of what number is 12?
This is an inverse percentage problem. We can solve it by setting up an equation:
0.20 * x = 12
x = 12 / 0.20
x = 60
Therefore, 20% of 60 is 12.
Advanced Concepts and Considerations
While the basic percentage calculations are straightforward, more advanced scenarios may involve compound percentages, percentage changes, and percentage points. Understanding these concepts is crucial for more complex applications.
Compound Percentages:
Compound percentages involve calculating percentages of percentages. For instance, calculating the final price after multiple discounts or the effect of compound interest over multiple periods requires understanding how to compound percentages correctly.
Percentage Change:
Percentage change describes the relative change between two values. It's calculated as:
[(New Value - Old Value) / Old Value] * 100%
Understanding percentage change is vital for analyzing trends and growth in various fields.
Percentage Points:
Percentage points refer to the arithmetic difference between two percentages. It's not the same as a percentage change. For example, if a value increases from 10% to 20%, the percentage increase is 100%, but the increase in percentage points is 10.
Conclusion
Calculating "8 is what percent of 11" is a fundamental percentage problem with numerous real-world applications. Mastering this type of calculation is essential for navigating various aspects of daily life and professional fields. By understanding the different methods for calculating percentages and exploring related problems, you'll develop a strong foundation in percentage calculations, empowering you to confidently tackle similar problems and interpret data effectively. Remember to choose the method that best suits your needs and always double-check your work to ensure accuracy.
Latest Posts
Latest Posts
-
What Is 10 Percent Of 10 Thousand Dollars
May 24, 2025
-
What Fraction Of 1 2 Is 1 3
May 24, 2025
-
What Percentage Is 4 Out Of 24
May 24, 2025
-
Fit By Katy Macro Calculator Free
May 24, 2025
-
5 1 4 As An Improper Fraction
May 24, 2025
Related Post
Thank you for visiting our website which covers about 8 Is What Percent Of 11 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.