8 Divided By 5 As A Fraction
listenit
May 21, 2025 · 4 min read
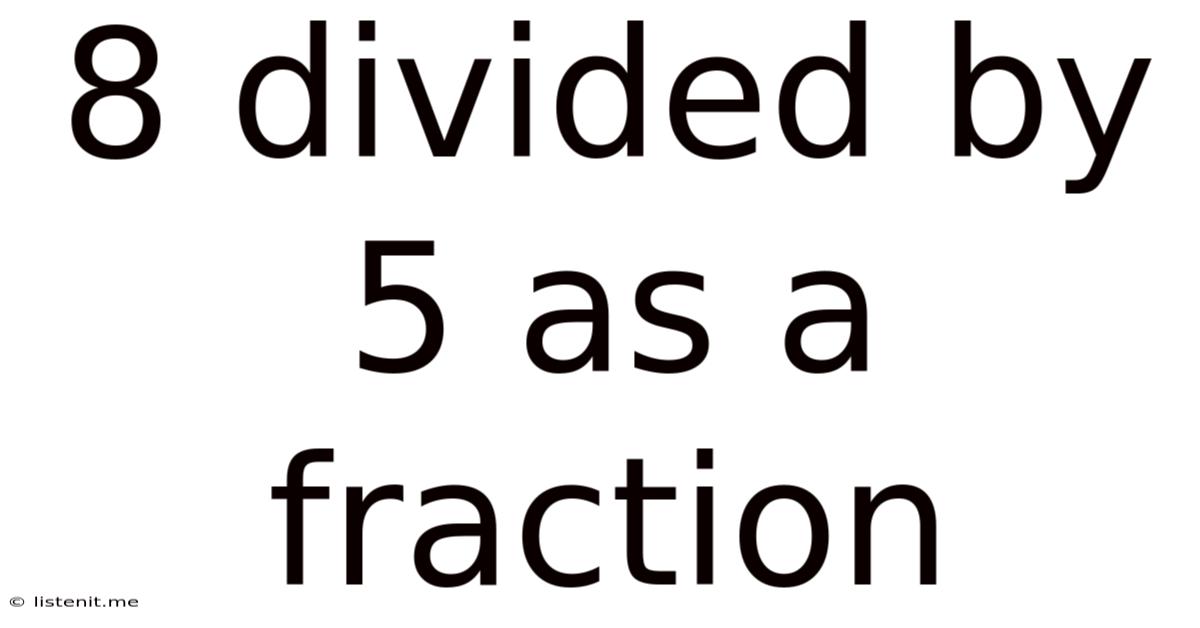
Table of Contents
8 Divided by 5 as a Fraction: A Comprehensive Guide
Understanding fractions is fundamental to mathematics, forming the bedrock for more advanced concepts. This comprehensive guide delves into the seemingly simple problem of 8 divided by 5 as a fraction, exploring various approaches and highlighting the underlying principles. We'll move beyond a simple answer to provide a deep understanding of the process and its applications.
Understanding Division and Fractions
Before tackling 8 divided by 5, let's solidify our understanding of division and fractions. Division, at its core, is the process of splitting a quantity into equal parts. A fraction, on the other hand, represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The denominator indicates the total number of equal parts the whole is divided into, while the numerator indicates how many of those parts are being considered.
For example, the fraction 3/4 represents 3 parts out of a total of 4 equal parts.
Expressing 8 Divided by 5 as a Fraction
The problem "8 divided by 5" can be expressed as a fraction directly. The dividend (the number being divided, 8) becomes the numerator, and the divisor (the number dividing, 5) becomes the denominator. Therefore, 8 divided by 5 as a fraction is written as:
8/5
This fraction is an improper fraction because the numerator (8) is larger than the denominator (5). Improper fractions represent a value greater than one.
Converting Improper Fractions to Mixed Numbers
Improper fractions are often converted into mixed numbers for easier understanding and representation. A mixed number combines a whole number and a proper fraction (where the numerator is smaller than the denominator).
To convert 8/5 to a mixed number, we perform the division:
8 ÷ 5 = 1 with a remainder of 3.
This means that 8/5 contains one whole group of 5 and 3 remaining parts out of 5. Therefore, 8/5 as a mixed number is:
1 3/5
This signifies one whole and three-fifths.
Visualizing 8/5
Visualizing fractions can significantly aid understanding. Imagine you have 8 identical items (e.g., pizzas). If you want to divide them equally among 5 people, each person would receive 8/5 of a pizza. This is equivalent to each person getting 1 whole pizza and 3/5 of another.
You can also visualize this using diagrams. Draw five rectangles representing the five people. Divide each rectangle into five equal parts. Then, distribute the eight items across these diagrams until you’ve used all 8 items. You'll find that each person receives one full rectangle and an additional 3 parts (out of five).
Decimal Representation
Fractions can also be expressed as decimals. To convert 8/5 to a decimal, perform the division:
8 ÷ 5 = 1.6
This means that 8/5 is equal to 1.6.
Equivalent Fractions
It's important to note that 8/5 is not the only way to represent this value as a fraction. There are infinitely many equivalent fractions. An equivalent fraction is a fraction that has the same value as the original fraction but with a different numerator and denominator. We can obtain equivalent fractions by multiplying both the numerator and the denominator by the same non-zero number.
For example:
- Multiplying both numerator and denominator by 2: (8 x 2) / (5 x 2) = 16/10
- Multiplying both numerator and denominator by 3: (8 x 3) / (5 x 3) = 24/15
These fractions, 16/10 and 24/15, are all equivalent to 8/5. They all simplify back down to 8/5.
Applications of 8/5
Understanding how to represent 8 divided by 5 as a fraction has practical applications across various fields:
Everyday Life:
- Sharing resources: Dividing 8 cookies among 5 friends.
- Cooking: Following a recipe that requires 8/5 cups of flour.
- Measurement: Measuring 8/5 meters of fabric.
Mathematics:
- Algebra: Solving equations involving fractions.
- Calculus: Working with limits and derivatives.
- Geometry: Calculating areas and volumes.
Other Fields:
- Engineering: Designing structures and machines.
- Computer science: Programming algorithms and data structures.
- Finance: Calculating interest and returns.
Solving Related Problems
The principles applied to 8 divided by 5 can be extended to other division problems resulting in improper fractions. For example:
- 11 divided by 4: This results in the improper fraction 11/4, which can be converted to the mixed number 2 ¾.
- 15 divided by 7: This gives the improper fraction 15/7, which converts to the mixed number 2 1/7.
By understanding the conversion between improper fractions and mixed numbers, and the concept of equivalent fractions, you can confidently tackle a wide range of division problems involving fractions.
Conclusion
Understanding the representation of 8 divided by 5 as a fraction—whether as an improper fraction (8/5), a mixed number (1 3/5), or a decimal (1.6)—is crucial for mathematical proficiency and real-world problem-solving. The ability to convert between these forms and understand the underlying concepts of division and fractions provides a solid foundation for more advanced mathematical concepts and applications across various disciplines. This detailed exploration moves beyond the simple answer, offering a comprehensive understanding of the process and its practical implications. Remember to always practice and solidify your understanding through various exercises to build confidence and mastery in working with fractions.
Latest Posts
Latest Posts
-
Coarctation Of The Aorta Preductal Vs Postductal
Jun 05, 2025
-
How Does Nac Affect Liver Function Tests
Jun 05, 2025
-
Nursing Care End Stage Liver Disease
Jun 05, 2025
-
Why Is Dlco Increased In Asthma
Jun 05, 2025
-
When To Use A Multiple Regression Analysis
Jun 05, 2025
Related Post
Thank you for visiting our website which covers about 8 Divided By 5 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.