8 9 Divided By 2 3
listenit
May 24, 2025 · 5 min read
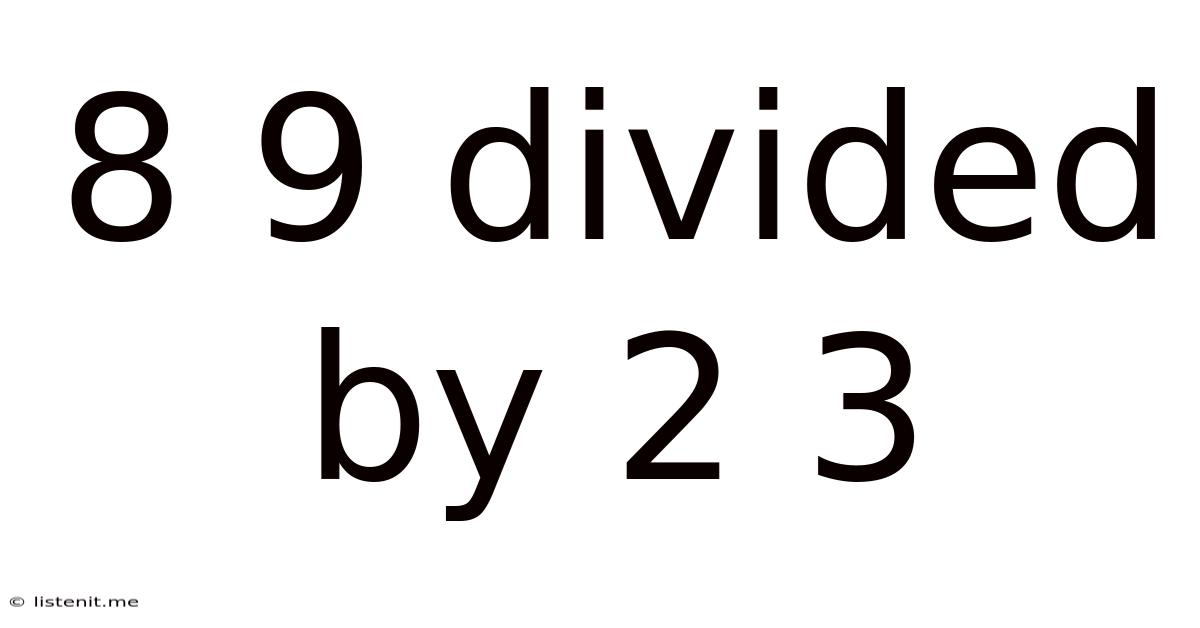
Table of Contents
Decoding the Enigma: A Deep Dive into 89 ÷ 23
The seemingly simple mathematical expression "89 divided by 23" hides a surprising depth of exploration, encompassing not just the straightforward answer but also delving into the underlying principles of division, its applications in various fields, and even its representation in different mathematical systems. This article aims to unravel this seemingly simple problem, transforming it into a journey of mathematical discovery.
The Straightforward Answer: Obtaining the Quotient and Remainder
The most immediate task is to find the quotient (the result of the division) and the remainder (the amount left over). Using long division, we discover that:
89 ÷ 23 ≈ 3 with a remainder of 20
This means that 23 goes into 89 three times, with 20 left over. We can represent this mathematically as:
89 = 23 x 3 + 20
This simple equation encapsulates the essence of division: breaking a larger number (the dividend, 89) into smaller equal parts (the divisor, 23), determining how many times the smaller part fits into the larger, and identifying any leftover (the remainder).
Beyond the Basics: Exploring the Concept of Division
Division, at its core, is the inverse operation of multiplication. While multiplication combines quantities, division separates a quantity into equal parts. This fundamental concept finds application across numerous real-world scenarios:
- Sharing Resources: Dividing a pizza among friends, allocating tasks among team members, or distributing resources fairly all involve division.
- Measurement and Scaling: Calculating the number of tiles needed to cover a floor, determining the amount of fabric required for a garment, or scaling recipes for different numbers of servings heavily rely on division.
- Data Analysis and Statistics: Calculating averages, percentages, and ratios, crucial in data analysis, uses division extensively. Consider calculating batting averages in baseball, or the average rainfall over a period of time.
- Computer Science and Programming: Division plays a crucial role in algorithms, data structures, and programming logic. For instance, it's used for array indexing, hash table implementation, and handling data in various formats.
Understanding the Remainder: Its Significance and Applications
While the quotient provides the primary answer, the remainder often holds significant information. Its significance varies depending on the context:
- Discrete Quantities: When dealing with discrete quantities (items that can be counted individually, like apples or people), the remainder represents the leftover items after equal distribution. For example, if you divide 89 candies among 23 children equally, each child gets 3 candies, and you have 20 candies remaining.
- Modular Arithmetic: In modular arithmetic (also known as clock arithmetic), the remainder is crucial. For example, in a 12-hour clock system, adding 14 hours is equivalent to adding 2 hours (14 mod 12 = 2, where "mod" denotes the modulo operation). The remainder after dividing by the modulus (in this case, 12) gives the equivalent time. This has applications in cryptography and computer science.
- Cyclic Patterns: The remainder can help identify patterns that repeat themselves after a certain interval. For example, in understanding periodic functions or repetitive sequences.
Expanding the Horizons: Decimal Representation and Fractions
While the division of 89 by 23 yields a whole-number quotient and a remainder, we can express the result more precisely using decimal representation or fractions:
- Decimal Representation: Using a calculator, we get:
89 ÷ 23 ≈ 3.869565...
This decimal representation extends infinitely, indicating that the result is a non-terminating, non-repeating decimal. The precision of this decimal depends on the number of decimal places used.
- Fraction Representation: We can represent the result as a mixed fraction:
3 20/23
This mixed fraction concisely captures both the whole number part (3) and the fractional part (20/23). This representation is particularly useful when working with exact values rather than approximations.
Applying the Concept: Real-World Examples
Let's illustrate the application of dividing 89 by 23 in different contexts:
Scenario 1: Resource Allocation
Imagine you have 89 liters of juice to distribute equally among 23 classrooms. Each classroom receives approximately 3.87 liters of juice. This highlights the practicality of the decimal representation. However, for practical purposes, you would likely distribute 3 liters to each classroom, with 20 liters remaining.
Scenario 2: Pricing and Discounts
Suppose a product costs $89 and is on sale with a 23% discount. To calculate the discount amount, you'd multiply 89 by (23/100) = 20.47. Rounding up to the nearest cent, the discount is $20.47.
Scenario 3: Data Analysis
Imagine you're analyzing the test scores of 23 students. The total score is 890. To find the average score, you'd divide 890 by 23, resulting in an average score of approximately 38.7.
Advanced Concepts: Beyond Basic Arithmetic
The seemingly simple division of 89 by 23 opens doors to more advanced mathematical concepts:
- Number Theory: The concepts of prime numbers, divisibility, and modular arithmetic are intricately connected to division. The properties of 89 and 23 (whether they are prime or composite) influence the nature of the division result.
- Algebra: Division forms the basis of solving equations and algebraic expressions. For example, solving equations like 23x = 89 involves dividing both sides by 23.
- Calculus: Division plays a crucial role in concepts such as derivatives and integrals, where the process of finding instantaneous rates of change or areas under curves often involves dividing infinitesimally small quantities.
Conclusion: The Enduring Importance of Division
The seemingly simple act of dividing 89 by 23 provides a pathway to a rich understanding of mathematical concepts. From basic arithmetic operations to advanced mathematical fields, division is an indispensable tool that underpins various aspects of mathematics and its applications in the real world. Understanding its nuances, including the significance of the quotient and remainder, and its various representations (decimal, fraction, mixed fraction) allows for greater flexibility and precision in solving a wide range of problems across diverse fields. The seemingly simple calculation is, therefore, far more profound than it initially appears, serving as a gateway to deeper mathematical insights.
Latest Posts
Latest Posts
-
What Is An 80 Out Of 100 On A Grade
May 24, 2025
-
How Tall Do You Have To Be
May 24, 2025
-
Round 25 To The Nearest Tenth
May 24, 2025
-
How Much Is 25 Off Of 50
May 24, 2025
-
What Time Is It In 22 Hours
May 24, 2025
Related Post
Thank you for visiting our website which covers about 8 9 Divided By 2 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.