8/7 Divided By 5/8 In Simplest Form
listenit
May 12, 2025 · 5 min read
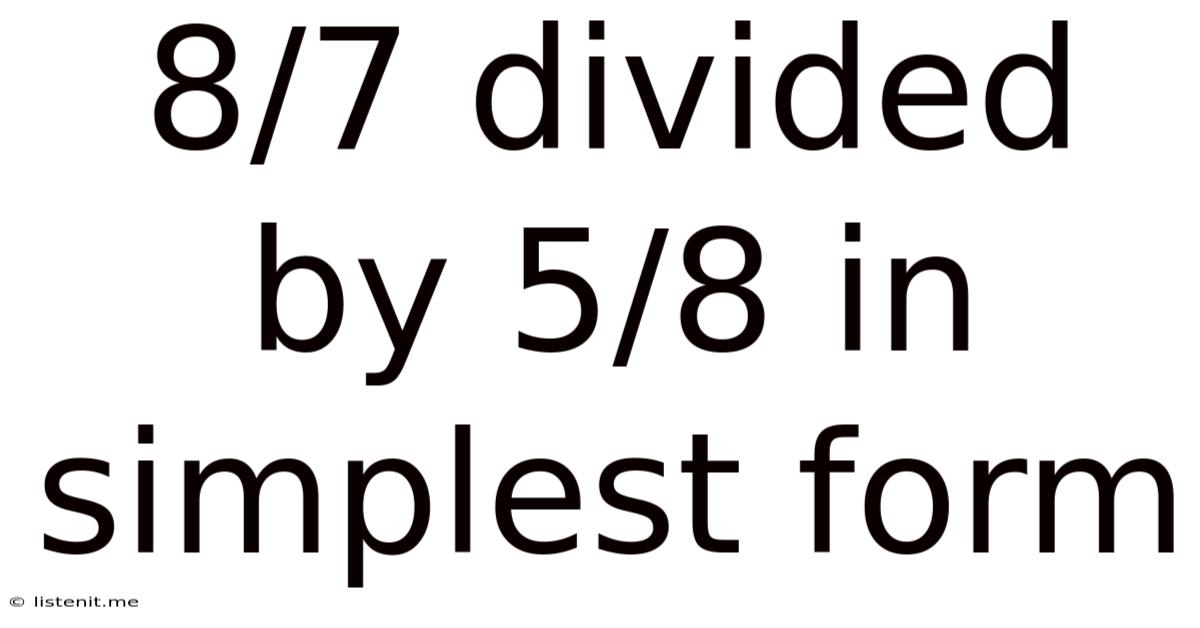
Table of Contents
8/7 Divided by 5/8 in Simplest Form: A Comprehensive Guide
Dividing fractions can seem daunting, but with a clear understanding of the process and a bit of practice, it becomes straightforward. This article will delve into the detailed solution of 8/7 divided by 5/8, explaining each step thoroughly and providing valuable insights into fraction division in general. We'll also explore related concepts to solidify your understanding and build your confidence in tackling similar problems.
Understanding Fraction Division
Before we tackle the specific problem, let's review the fundamental concept of dividing fractions. The key is to remember that dividing by a fraction is the same as multiplying by its reciprocal. The reciprocal of a fraction is simply the fraction flipped upside down. For example, the reciprocal of 2/3 is 3/2, and the reciprocal of 5/8 is 8/5.
Therefore, the general rule for dividing fractions is:
a/b ÷ c/d = a/b x d/c
This rule forms the bedrock of our solution. We'll apply this principle to solve 8/7 divided by 5/8.
Solving 8/7 Divided by 5/8 Step-by-Step
Here's a step-by-step breakdown of how to solve 8/7 ÷ 5/8:
Step 1: Find the reciprocal of the second fraction (the divisor).
The second fraction in our problem is 5/8. Its reciprocal is 8/5.
Step 2: Rewrite the division problem as a multiplication problem.
Following our rule, we replace the division sign with a multiplication sign and use the reciprocal of the second fraction:
8/7 ÷ 5/8 = 8/7 x 8/5
Step 3: Multiply the numerators (top numbers) together.
8 x 8 = 64
Step 4: Multiply the denominators (bottom numbers) together.
7 x 5 = 35
Step 5: Write the result as a single fraction.
Combining the results from steps 3 and 4, we get:
64/35
Step 6: Simplify the fraction (if possible).
In this case, 64 and 35 don't share any common factors other than 1. Therefore, the fraction 64/35 is already in its simplest form.
Therefore, the solution to 8/7 divided by 5/8 is 64/35.
Beyond the Calculation: Understanding the Result
The result, 64/35, is an improper fraction (the numerator is larger than the denominator). This is perfectly acceptable, but it can also be expressed as a mixed number. Let's convert it:
To convert an improper fraction to a mixed number, we divide the numerator by the denominator.
64 ÷ 35 = 1 with a remainder of 29.
Therefore, 64/35 can be written as the mixed number 1 29/35.
Practical Applications and Real-World Examples
Understanding fraction division is crucial in numerous real-world scenarios. Here are a few examples:
-
Cooking and Baking: Recipes often require dividing ingredients. For instance, if a recipe calls for 5/8 cup of flour and you want to make only half the recipe, you'd divide 5/8 by 2 (or 2/1), which is equivalent to multiplying 5/8 by 1/2.
-
Sewing and Crafts: Cutting fabric or other materials often involves dividing lengths into fractions.
-
Construction and Engineering: Precise measurements and calculations using fractions are essential in various construction and engineering projects.
-
Data Analysis: Working with datasets frequently involves calculations using fractions and understanding proportions.
Further Exploration: Different Methods and Strategies
While the reciprocal method is the most common and efficient way to divide fractions, it's beneficial to understand alternative approaches.
One such method involves converting the fractions to decimals before performing the division. However, this approach can sometimes lead to rounding errors and might not result in the simplest form of the answer.
Troubleshooting Common Errors
When working with fractions, several common mistakes can occur:
-
Forgetting to find the reciprocal: This is the most common error. Remember, you must use the reciprocal of the second fraction when converting division to multiplication.
-
Incorrect multiplication: Double-check your multiplication of both the numerators and denominators.
-
Failing to simplify: Always simplify your final answer to its lowest terms by finding the greatest common divisor (GCD) of the numerator and denominator.
Mastering Fraction Division: Tips and Practice
Mastering fraction division requires consistent practice. Here are some tips:
-
Start with simpler problems: Begin with easier fraction division problems before tackling more complex ones.
-
Use visual aids: Diagrams and models can be helpful, especially when first learning about fractions.
-
Practice regularly: Consistent practice is key to improving your skills and building confidence.
-
Seek help when needed: Don't hesitate to ask for assistance from a teacher, tutor, or online resource if you encounter difficulties.
Expanding Your Knowledge: Related Concepts
To further enhance your understanding, explore these related concepts:
-
Greatest Common Divisor (GCD): Understanding how to find the GCD is crucial for simplifying fractions to their simplest form.
-
Least Common Multiple (LCM): The LCM is vital when adding or subtracting fractions with different denominators.
-
Improper and Mixed Fractions: Understanding the conversion between these fraction types is essential for various calculations.
Conclusion
Dividing fractions, while initially appearing complex, becomes manageable with a solid understanding of the underlying principles. By following the step-by-step method outlined above and practicing regularly, you can confidently solve problems like 8/7 divided by 5/8 and apply this knowledge to various real-world scenarios. Remember to always simplify your final answer and to check for common errors. With consistent effort and practice, you will master fraction division and build a strong foundation in mathematics.
Latest Posts
Related Post
Thank you for visiting our website which covers about 8/7 Divided By 5/8 In Simplest Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.