7 Is 1/10 Of What Number
listenit
May 24, 2025 · 4 min read
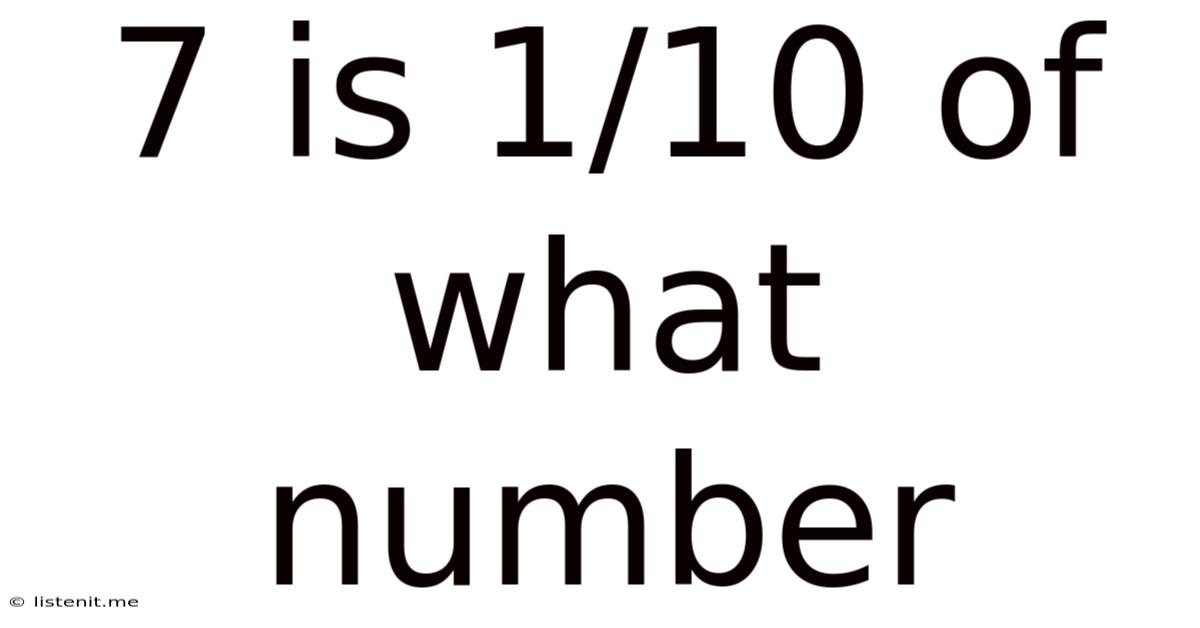
Table of Contents
7 is 1/10 of What Number? Unlocking the Power of Fraction Equations
Welcome, math enthusiasts! Today, we're diving into a seemingly simple yet incredibly fundamental concept in mathematics: solving fraction equations. Specifically, we'll unravel the mystery behind the question: "7 is 1/10 of what number?" This seemingly straightforward problem serves as a gateway to understanding more complex algebraic concepts and their applications in various fields. We'll explore multiple methods to solve this, ensuring you grasp the underlying principles and can confidently tackle similar problems in the future.
Understanding the Problem: Deconstructing the Equation
Before we jump into solutions, let's break down the problem statement: "7 is 1/10 of what number?" This statement can be translated directly into a mathematical equation:
7 = (1/10) * x
Where 'x' represents the unknown number we're trying to find. This equation expresses the relationship between 7, the fraction 1/10, and the unknown number. Our goal is to isolate 'x' and determine its value.
Method 1: The Multiplication Method – A Direct Approach
This method leverages the fundamental properties of equations. To isolate 'x', we need to eliminate the (1/10) multiplying it. We can achieve this by multiplying both sides of the equation by the reciprocal of (1/10), which is 10:
10 * 7 = 10 * (1/10) * x
This simplifies to:
70 = x
Therefore, 7 is 1/10 of 70.
Verification: Checking Our Answer
It's crucial to verify our solution. Let's substitute x = 70 back into the original equation:
7 = (1/10) * 70
7 = 7
The equation holds true, confirming that our solution, x = 70, is correct.
Method 2: The Division Method – An Alternative Perspective
This method uses the concept of division to achieve the same result. The equation 7 = (1/10) * x can be interpreted as: "7 is one-tenth of x". To find x, we can ask, "What number, when divided by 10, equals 7?"
This translates to:
x / 10 = 7
To isolate x, we multiply both sides by 10:
x = 7 * 10
x = 70
Again, we arrive at the same solution: x = 70.
Verification: Reinforcing Our Understanding
Substituting x = 70 back into the original equation:
7 = (1/10) * 70
7 = 7
The equation is satisfied, validating our solution once more.
Method 3: Using Proportions – A Visual Approach
Proportions offer a visual and intuitive way to solve this type of problem. We can set up a proportion based on the given information:
7 / x = 1/10
This proportion states that the ratio of 7 to the unknown number (x) is equal to the ratio of 1 to 10. To solve this proportion, we can cross-multiply:
7 * 10 = 1 * x
70 = x
This confirms our previous solutions: x = 70.
Verification: Consistency in Results
Substituting x = 70 back into the original proportion:
7 / 70 = 1/10
1/10 = 1/10
The proportion holds true, further solidifying our understanding of the problem and its solution.
Expanding the Concept: Generalizing Fraction Equations
The problem "7 is 1/10 of what number?" is a specific example of a broader class of problems involving fraction equations. The general form of these equations is:
a = (b/c) * x
Where 'a', 'b', and 'c' are known constants, and 'x' is the unknown variable. To solve for 'x', we can use a similar approach as before:
Multiply both sides by the reciprocal of (b/c):
(c/b) * a = x
This formula provides a powerful tool for solving a wide variety of fraction equations. By substituting the specific values from our original problem (a = 7, b = 1, c = 10), we can derive the solution efficiently.
Real-World Applications: Where Fraction Equations Matter
Understanding fraction equations is not just about solving mathematical puzzles; it has significant practical applications across numerous fields:
-
Finance: Calculating percentages, interest rates, and discounts heavily relies on fraction equations. For instance, determining the principal amount based on a given interest and accumulated amount involves solving a fraction equation.
-
Engineering: In engineering design and calculations, scaling, ratios, and proportions are crucial. Fraction equations play a central role in ensuring accurate calculations and designs.
-
Science: Many scientific formulas and principles involve ratios and fractions. Solving for unknown variables frequently requires manipulating fraction equations.
-
Cooking and Baking: Adjusting recipes to accommodate different quantities relies on the principles of proportions and fractions.
-
Everyday Life: Numerous everyday situations, such as splitting bills, calculating sale prices, or determining the amount of ingredients needed for a recipe, involve understanding and applying the concepts of fractions and proportions.
Conclusion: Mastering Fraction Equations – A Stepping Stone to Success
Solving the equation "7 is 1/10 of what number?" is more than just finding the answer 70. It's about understanding the fundamental principles of fraction equations, which are crucial in various aspects of mathematics and beyond. By mastering these techniques, you gain a valuable skill set applicable across various disciplines and everyday situations. Remember, practice is key! The more you solve these types of problems, the more comfortable and confident you'll become in tackling complex mathematical challenges. So grab a pen and paper, work through some more examples, and enjoy the journey of mathematical discovery.
Latest Posts
Latest Posts
-
What Are The Common Factors Of 32 And 28
May 24, 2025
-
18 Is What Percent Of 25
May 24, 2025
-
How Long Is 5 Hours From Now
May 24, 2025
-
What Is 30 Percent Of 60 Dollars
May 24, 2025
-
What Is 15 Percent Of 350
May 24, 2025
Related Post
Thank you for visiting our website which covers about 7 Is 1/10 Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.