7/15 Divided By 3/10 In Simplest Form
listenit
May 24, 2025 · 5 min read
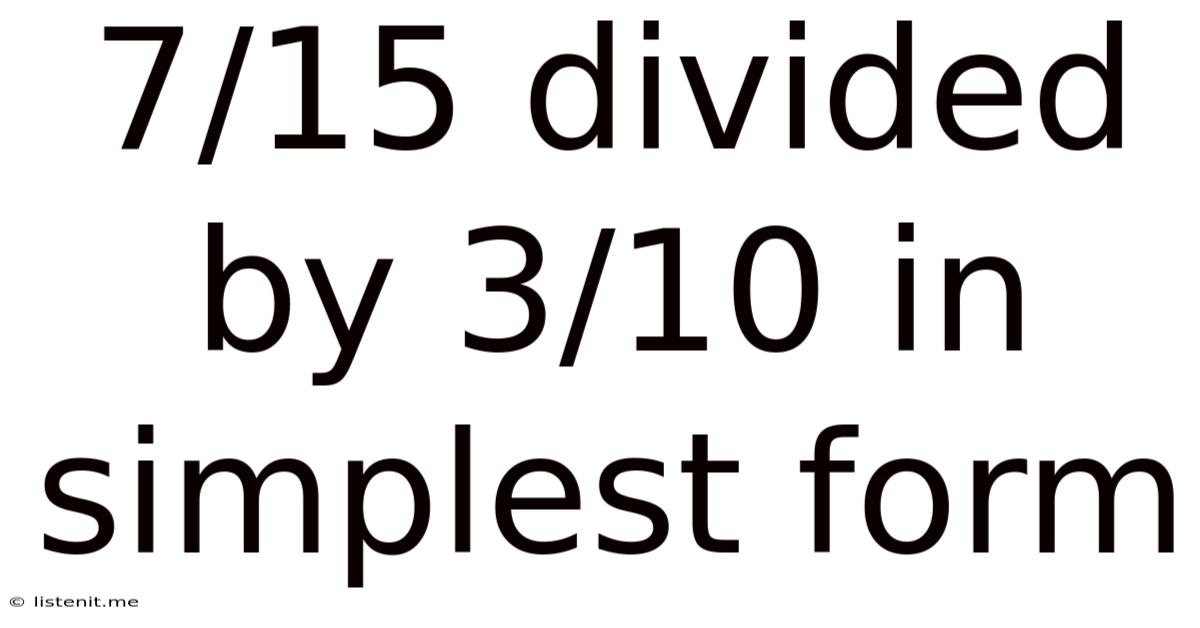
Table of Contents
7/15 Divided by 3/10 in Simplest Form: A Comprehensive Guide
Dividing fractions can seem daunting, but with a clear understanding of the process and a few helpful strategies, it becomes a straightforward task. This comprehensive guide will walk you through dividing 7/15 by 3/10, explaining the steps involved and demonstrating how to simplify the result to its simplest form. We'll explore the underlying mathematical principles and provide practical tips to boost your fraction skills.
Understanding Fraction Division
Before we tackle our specific problem (7/15 ÷ 3/10), let's refresh our understanding of fraction division. The fundamental principle is to invert the second fraction (the divisor) and multiply. This is equivalent to multiplying by the reciprocal.
The reciprocal of a fraction is simply the fraction flipped upside down. For example, the reciprocal of 3/10 is 10/3.
Therefore, dividing by a fraction is the same as multiplying by its reciprocal. This simple rule transforms a division problem into a multiplication problem, which is often easier to handle.
The Process in Three Steps
To divide fractions, follow these three simple steps:
- Invert the second fraction (divisor): Flip the numerator and denominator.
- Change the division sign to a multiplication sign: Replace the division symbol (÷) with a multiplication symbol (×).
- Multiply the numerators and multiply the denominators: Simplify the resulting fraction if possible.
Solving 7/15 Divided by 3/10
Now, let's apply this process to our problem: 7/15 ÷ 3/10
Step 1: Invert the divisor (3/10)
The reciprocal of 3/10 is 10/3.
Step 2: Change the division sign to multiplication
Our problem now becomes: 7/15 × 10/3
Step 3: Multiply the numerators and denominators
Multiply the numerators (top numbers) together: 7 × 10 = 70 Multiply the denominators (bottom numbers) together: 15 × 3 = 45
This gives us the fraction: 70/45
Simplifying the Fraction
The fraction 70/45 is not in its simplest form. To simplify a fraction, we need to find the greatest common divisor (GCD) of the numerator and the denominator. The GCD is the largest number that divides both the numerator and denominator without leaving a remainder.
We can find the GCD using several methods, including:
- Listing factors: List all the factors of 70 and 45 and identify the largest common factor.
- Prime factorization: Break down both numbers into their prime factors and find the common factors.
- Euclidean algorithm: A more efficient method for larger numbers.
Let's use prime factorization to find the GCD of 70 and 45:
- Prime factorization of 70: 2 × 5 × 7
- Prime factorization of 45: 3 × 3 × 5
The common factor is 5.
Now, divide both the numerator and the denominator by the GCD (5):
70 ÷ 5 = 14 45 ÷ 5 = 9
Therefore, the simplified fraction is 14/9.
Expressing the Answer as a Mixed Number
The fraction 14/9 is an improper fraction because the numerator (14) is larger than the denominator (9). We can convert this improper fraction into a mixed number, which consists of a whole number and a proper fraction.
To do this, divide the numerator (14) by the denominator (9):
14 ÷ 9 = 1 with a remainder of 5
The quotient (1) becomes the whole number part, and the remainder (5) becomes the numerator of the fraction, while the denominator remains the same (9).
So, 14/9 as a mixed number is 1 5/9.
Practical Applications and Real-World Examples
Understanding fraction division isn't just an academic exercise; it has numerous practical applications in everyday life. Here are a few examples:
-
Cooking and Baking: Many recipes require precise measurements. If a recipe calls for 3/4 cup of flour, and you only want to make 1/2 of the recipe, you'll need to divide 3/4 by 2 (or multiply by 1/2), resulting in 3/8 cup of flour.
-
Sewing and Crafting: If you need to cut a piece of fabric that is 7/8 yards long into three equal pieces, you'll need to divide 7/8 by 3.
-
Construction and Engineering: Precise measurements and calculations are crucial in construction and engineering projects. Dividing fractions is often necessary for tasks such as calculating the amount of material needed for a project or determining the dimensions of components.
-
Data Analysis: In data analysis and statistics, fractions are commonly used to represent proportions and ratios. Dividing fractions is essential for comparing and analyzing these proportions.
Tips and Tricks for Mastering Fraction Division
-
Practice Regularly: The key to mastering fraction division is consistent practice. Work through various problems, starting with simple ones and gradually increasing the complexity.
-
Visual Aids: Use visual aids like diagrams or fraction bars to help visualize the process of dividing fractions.
-
Simplify Before Multiplying: Simplifying fractions before multiplying can make the calculations easier. Look for common factors in the numerators and denominators and cancel them out before performing the multiplication.
-
Check Your Work: Always check your answer to make sure it's reasonable. Estimate the answer before you start calculating to ensure your final answer is in the right ballpark.
Conclusion
Dividing fractions, while initially seeming challenging, becomes manageable with a systematic approach. By understanding the process of inverting and multiplying, simplifying fractions, and converting between improper fractions and mixed numbers, you can confidently tackle any fraction division problem, including the example of 7/15 divided by 3/10, which simplifies to 14/9 or 1 5/9. Remember to practice regularly and utilize helpful strategies to build your proficiency and confidence in working with fractions. Mastering this skill opens doors to a broader understanding of mathematics and its numerous real-world applications.
Latest Posts
Latest Posts
-
How Many Btu To Heat 900 Sq Ft
May 24, 2025
-
Where Is The Calculator On The Ww App
May 24, 2025
-
What Is 30 Percent Of 125
May 24, 2025
-
Greatest Common Factor Of 24 And 84
May 24, 2025
-
20 Divided By 3 In Fraction
May 24, 2025
Related Post
Thank you for visiting our website which covers about 7/15 Divided By 3/10 In Simplest Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.