6x 3y 12 In Slope Intercept Form
listenit
May 09, 2025 · 6 min read
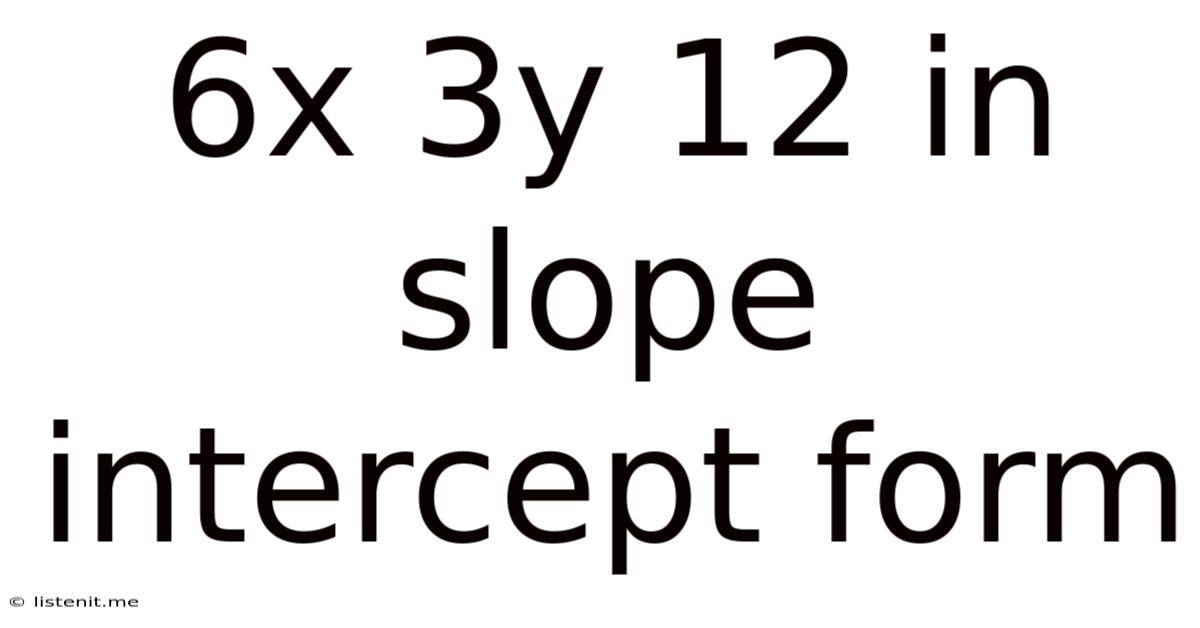
Table of Contents
Converting 6x + 3y = 12 to Slope-Intercept Form: A Comprehensive Guide
The equation 6x + 3y = 12 represents a linear relationship between x and y. While useful in its current form, converting it to slope-intercept form (y = mx + b) offers significant advantages in understanding and visualizing the line it represents. This form explicitly reveals the slope (m) and the y-intercept (b) of the line. This guide will walk you through the step-by-step process of this conversion, exploring the underlying concepts and providing practical applications.
Understanding Slope-Intercept Form (y = mx + b)
Before diving into the conversion, let's solidify our understanding of the slope-intercept form: y = mx + b.
- y: Represents the dependent variable. Its value depends on the value of x.
- x: Represents the independent variable. We can choose any value for x.
- m: Represents the slope of the line. The slope indicates the steepness and direction of the line. A positive slope indicates an upward trend from left to right, while a negative slope indicates a downward trend. The slope is calculated as the change in y divided by the change in x (rise over run).
- b: Represents the y-intercept. This is the point where the line intersects the y-axis (where x = 0).
Converting 6x + 3y = 12 to Slope-Intercept Form
The goal is to isolate 'y' on one side of the equation. Let's break down the process:
-
Subtract 6x from both sides:
This step removes the '6x' term from the left side, moving it to the right:
3y = -6x + 12
-
Divide both sides by 3:
This isolates 'y', giving us the slope-intercept form:
y = -2x + 4
Therefore, the slope-intercept form of the equation 6x + 3y = 12 is y = -2x + 4.
Analyzing the Slope and y-intercept
Now that we have the equation in slope-intercept form, we can easily extract valuable information:
-
Slope (m) = -2: This negative slope indicates that the line slopes downwards from left to right. For every one unit increase in x, y decreases by two units.
-
y-intercept (b) = 4: This means the line crosses the y-axis at the point (0, 4).
Graphical Representation
The slope-intercept form makes graphing the line incredibly straightforward. We can use the y-intercept as our starting point and then use the slope to plot additional points.
-
Plot the y-intercept: Start by plotting the point (0, 4) on the coordinate plane.
-
Use the slope to find another point: Since the slope is -2 (or -2/1), we can move down 2 units and to the right 1 unit from the y-intercept (0,4). This gives us the point (1, 2). Alternatively, you could move up 2 units and to the left 1 unit to obtain the point (-1, 6).
-
Draw the line: Draw a straight line through the points (0, 4) and (1, 2) (or (-1,6)). This line represents the equation 6x + 3y = 12.
Applications and Practical Uses
Understanding linear equations in slope-intercept form has numerous practical applications across various fields:
-
Economics: Modeling supply and demand curves, analyzing cost functions, and predicting economic trends. The slope might represent the price elasticity of demand, while the intercept could represent fixed costs.
-
Physics: Describing motion with constant velocity or acceleration, analyzing relationships between force, mass, and acceleration. The slope could represent velocity, and the intercept could represent initial position.
-
Engineering: Designing slopes for roads and ramps, calculating gradients, and analyzing structural stability. The slope is crucial in determining the angle of inclination.
-
Computer Science: Representing linear relationships in algorithms and data structures, performing linear transformations in image processing.
-
Statistics: Regression analysis uses linear equations to model the relationship between variables. The slope represents the regression coefficient, indicating the strength and direction of the relationship.
Solving Problems Using Slope-Intercept Form
The slope-intercept form simplifies solving various problems related to linear equations:
1. Finding the y-coordinate given an x-coordinate:
If you need to find the y-value for a specific x-value, simply substitute the x-value into the equation and solve for y. For example, if x = 2, then y = -2(2) + 4 = 0. Therefore, the point (2,0) lies on the line.
2. Finding the x-coordinate given a y-coordinate:
Similarly, you can solve for x if you are given a y-value. For example, if y = 0, then 0 = -2x + 4, which means 2x = 4, so x = 2. This confirms the point we found earlier (2,0).
3. Determining if a point lies on the line:
To check if a given point (x, y) lies on the line, substitute the x and y values into the equation. If the equation holds true, the point lies on the line. For example, let's check the point (3,-2): -2 = -2(3) + 4 which simplifies to -2 = -2. This confirms (3,-2) is on the line.
4. Comparing slopes of different lines:
By comparing the slopes of two lines in slope-intercept form, you can determine if the lines are parallel (same slope), perpendicular (slopes are negative reciprocals), or neither.
5. Finding the equation of a parallel or perpendicular line:
Knowing the slope of a given line, you can readily find the equation of a line that is parallel or perpendicular to it. A parallel line will have the same slope, while a perpendicular line will have a slope that is the negative reciprocal.
Beyond the Basics: Standard Form and Other Representations
While the slope-intercept form is highly useful, it's important to understand that linear equations can be represented in other forms:
-
Standard Form (Ax + By = C): This form, where A, B, and C are constants, is useful for certain applications and can easily be converted to slope-intercept form. The equation 6x + 3y = 12 is already in standard form.
-
Point-Slope Form (y - y1 = m(x - x1)): This form uses a point (x1, y1) on the line and the slope (m) to represent the equation. It's particularly useful when you know a point and the slope.
Understanding the relationship between these different forms allows for flexibility in solving problems and choosing the most appropriate representation for a given context.
Conclusion
Converting the equation 6x + 3y = 12 to slope-intercept form (y = -2x + 4) provides a clear and concise representation of the linear relationship between x and y. This form facilitates understanding the line's slope, y-intercept, and graphical representation, significantly aiding problem-solving in various fields. Mastering this conversion, along with understanding the other forms of linear equations, empowers you to effectively analyze and utilize linear relationships in diverse applications. Remember to practice regularly to solidify your understanding and build confidence in working with linear equations.
Latest Posts
Latest Posts
-
50 Divided By A Number F
May 09, 2025
-
Animals That Live On Land And Water Are Called
May 09, 2025
-
How Many Atp Molecules Are Produced During The Krebs Cycle
May 09, 2025
-
Density Of Phosphoric Acid G Ml
May 09, 2025
-
What Is The Molarity Of Concentrated Hcl
May 09, 2025
Related Post
Thank you for visiting our website which covers about 6x 3y 12 In Slope Intercept Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.