65 Is What Percent Of 80
listenit
May 10, 2025 · 4 min read
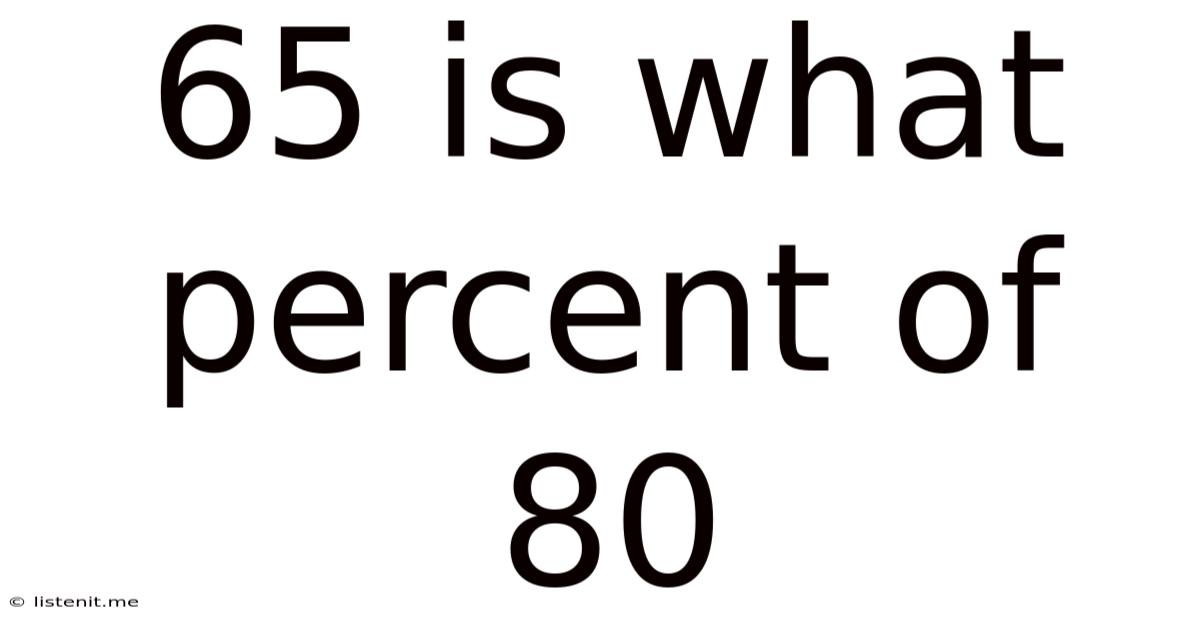
Table of Contents
65 is What Percent of 80? A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill with wide-ranging applications in various aspects of life, from everyday budgeting and shopping to more complex scenarios in finance, science, and statistics. Understanding how to solve percentage problems, like determining what percent 65 is of 80, is crucial for making informed decisions and accurately interpreting data. This comprehensive guide will not only provide the answer to this specific question but also delve into the underlying principles and techniques for tackling similar percentage problems. We'll explore various methods, including the formula approach, the proportion method, and the practical applications of percentage calculations.
Understanding Percentages
A percentage is a fraction or a ratio expressed as a number out of 100. The symbol "%" represents "per cent," meaning "out of one hundred." Therefore, 25% means 25 out of 100, which can also be written as the fraction 25/100 or the decimal 0.25. Percentages provide a standardized way to compare different proportions and make data easier to understand and interpret.
Method 1: The Formula Approach
The most straightforward method to determine what percent 65 is of 80 is using the basic percentage formula:
(Part / Whole) x 100 = Percentage
In this case:
- Part: 65
- Whole: 80
Substituting these values into the formula:
(65 / 80) x 100 = Percentage
Calculating this gives us:
0.8125 x 100 = 81.25%
Therefore, 65 is 81.25% of 80.
Method 2: The Proportion Method
This method uses proportions to solve percentage problems. A proportion is an equation stating that two ratios are equal. We can set up a proportion as follows:
65/80 = x/100
Where 'x' represents the percentage we want to find. To solve for 'x', we cross-multiply:
65 * 100 = 80 * x
6500 = 80x
x = 6500 / 80
x = 81.25
Therefore, once again, we find that 65 is 81.25% of 80.
Practical Applications of Percentage Calculations
The ability to calculate percentages is invaluable in many real-life situations. Here are a few examples:
1. Retail Discounts and Sales
Stores frequently advertise discounts as percentages. For example, a "20% off" sale means that the price is reduced by 20% of the original price. Understanding percentage calculations allows consumers to quickly determine the final price after a discount.
2. Financial Calculations
Percentages are fundamental in finance. Interest rates on loans and savings accounts, tax calculations, and investment returns are all expressed as percentages. Accurate percentage calculations are essential for managing personal finances and making sound financial decisions.
3. Statistical Analysis
In statistics, percentages are used extensively to represent data proportions and trends. For example, opinion polls, survey results, and scientific research often present findings using percentages to show the relative frequency of different outcomes.
4. Grading and Assessment
In education, grades and test scores are often expressed as percentages, representing the proportion of correct answers or the overall performance level. Understanding percentage calculations helps students understand their academic progress and identify areas for improvement.
5. Scientific and Engineering Applications
Percentages are also used in various scientific and engineering fields to represent ratios, concentrations, and error rates. For example, in chemistry, concentration is often expressed as a percentage by weight or volume.
Solving Similar Percentage Problems
The methods described above can be applied to solve any percentage problem. To find what percent 'a' is of 'b', simply use the formula:
(a / b) x 100 = Percentage
Or set up a proportion:
a/b = x/100
And solve for 'x'.
Common Mistakes to Avoid
When working with percentages, it's essential to avoid common errors:
- Incorrect Formula: Using the wrong formula can lead to inaccurate results. Always double-check that you are using the appropriate formula for the specific percentage problem.
- Decimal Errors: Make sure to handle decimal values accurately during calculations. Rounding errors can accumulate and lead to significant inaccuracies in the final result.
- Misunderstanding the Problem: Carefully read and understand the problem statement to correctly identify the 'part' and the 'whole' before applying the percentage formula.
Mastering Percentage Calculations: Tips and Tricks
Here are some tips and tricks to improve your percentage calculation skills:
- Practice Regularly: The more you practice, the more comfortable and proficient you'll become. Work through various percentage problems to build your confidence and understanding.
- Use a Calculator: For more complex calculations, using a calculator can save time and improve accuracy.
- Learn Mental Math Techniques: Developing mental math skills for simple percentage calculations can enhance your speed and efficiency.
- Check Your Work: Always check your answer to ensure it makes sense in the context of the problem. If the result seems unreasonable, review your calculations to identify any errors.
Conclusion: The Power of Percentages
The ability to calculate percentages is a powerful tool with numerous real-world applications. Understanding the basic principles, formulas, and methods described in this guide will equip you to confidently tackle a wide range of percentage problems, improving your analytical skills and decision-making abilities in various aspects of your life. From managing personal finances to interpreting data and solving scientific problems, mastering percentage calculations is an invaluable asset. Remember the formula: (Part / Whole) x 100 = Percentage, and practice regularly to become proficient. By understanding the underlying concepts and techniques, you'll gain a solid foundation in percentage calculations and unlock their potential in many diverse situations.
Latest Posts
Latest Posts
-
What Are The Units For Measuring Specific Heat
May 10, 2025
-
A Dilation Is An Isometry True False
May 10, 2025
-
A 15 Ft Ladder Is Leaning Against A Wall
May 10, 2025
-
Calculate The Percentage Composition Of Nh4 2co3
May 10, 2025
-
What Is 22 Celsius In Degrees
May 10, 2025
Related Post
Thank you for visiting our website which covers about 65 Is What Percent Of 80 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.