60 Out Of 200 As A Percentage
listenit
May 11, 2025 · 4 min read
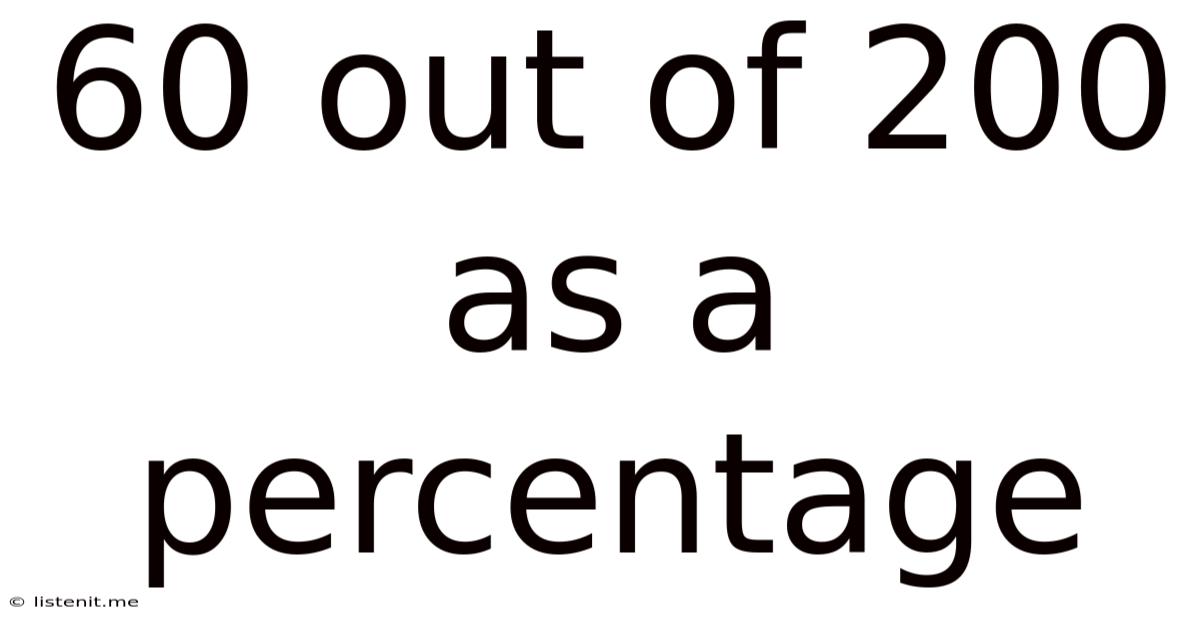
Table of Contents
60 out of 200 as a Percentage: A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill with widespread applications in various aspects of life, from everyday finances to complex scientific analyses. Understanding how to convert fractions and ratios into percentages is crucial for making informed decisions and interpreting data accurately. This comprehensive guide will delve into the specifics of calculating "60 out of 200 as a percentage," exploring different methods, providing practical examples, and offering insights into broader percentage applications.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The term "percent" is derived from the Latin "per centum," meaning "out of a hundred." Therefore, a percentage represents a portion or proportion of a whole, expressed as a number followed by the "%" symbol. For instance, 50% means 50 out of 100, or one-half.
Method 1: Using the Formula
The most straightforward way to calculate "60 out of 200 as a percentage" is by using the fundamental percentage formula:
(Part / Whole) * 100% = Percentage
In this case:
- Part: 60 (the number representing the portion)
- Whole: 200 (the total number representing the whole)
Substituting these values into the formula:
(60 / 200) * 100% = 30%
Therefore, 60 out of 200 is 30%.
Method 2: Simplifying the Fraction
Before applying the formula, we can simplify the fraction 60/200. Both the numerator (60) and the denominator (200) are divisible by 20:
60 ÷ 20 = 3 200 ÷ 20 = 10
This simplifies the fraction to 3/10. Now, we can easily convert this fraction to a percentage:
(3 / 10) * 100% = 30%
This method demonstrates that simplifying the fraction first can make the calculation easier and faster, especially when dealing with larger numbers.
Method 3: Using Decimal Conversion
Another approach involves converting the fraction to a decimal first and then multiplying by 100%:
60 / 200 = 0.3
0.3 * 100% = 30%
This method highlights the close relationship between decimals and percentages. Multiplying a decimal by 100% simply shifts the decimal point two places to the right.
Real-World Applications
The ability to calculate percentages has numerous practical applications across various fields:
Finance:
- Calculating interest rates: Understanding percentages is crucial for comprehending interest rates on loans, mortgages, savings accounts, and investments.
- Determining discounts: Retailers frequently advertise discounts as percentages (e.g., "30% off"). Knowing how to calculate these discounts helps consumers determine the final price.
- Analyzing financial statements: Financial statements often present data as percentages, allowing for comparisons between different periods or entities. For example, profit margins are expressed as a percentage of revenue.
- Calculating taxes: Taxes are commonly calculated as a percentage of income or the value of goods and services.
Science and Statistics:
- Data representation: Percentages are often used to represent data in charts, graphs, and tables, making it easier to visualize and interpret trends.
- Probability and statistics: Percentages are fundamental to expressing probabilities and statistical findings. For example, the probability of an event occurring might be expressed as a percentage.
- Scientific measurements: Percentages are used to express concentrations, errors, and changes in various scientific measurements.
Everyday Life:
- Calculating tips: Many people calculate tips in restaurants as a percentage of the bill (e.g., a 15% tip).
- Determining grades: In many educational systems, grades are expressed as percentages.
- Understanding survey results: Survey results are often presented as percentages to represent the proportion of respondents who chose a particular option.
Beyond the Basics: Advanced Percentage Calculations
While calculating "60 out of 200 as a percentage" is a relatively simple example, the concept of percentages extends to more complex calculations:
- Calculating percentage increase or decrease: This involves comparing two values to determine the percentage change between them. The formula is:
((New Value - Old Value) / Old Value) * 100% - Finding the percentage of a number: This involves calculating a specific percentage of a given number. For example, finding 25% of 80.
- Determining the original value after a percentage change: This involves working backward from a percentage change to determine the original value.
Practical Examples using 60 out of 200
Let's explore a few real-world scenarios using the 30% we derived from "60 out of 200":
Scenario 1: Exam Scores
A student answered 60 questions correctly out of a total of 200 questions on an exam. Their score is 30%.
Scenario 2: Sales Performance
A salesperson achieved 60 sales out of a target of 200 sales. Their sales performance is 30% of their target.
Scenario 3: Survey Results
In a survey of 200 people, 60 responded positively to a specific question. The positive response rate is 30%.
Scenario 4: Production Efficiency
A factory produced 60 units of a product out of a planned production of 200 units. The production efficiency is 30%.
Conclusion
Calculating percentages is an essential skill applicable across numerous domains. Understanding the different methods for calculating percentages, including the formula method, fraction simplification, and decimal conversion, empowers individuals to confidently tackle various percentage-related problems. The ability to interpret and utilize percentage data is key to informed decision-making in both personal and professional contexts. Mastering percentage calculations equips you with a powerful tool for navigating the quantitative aspects of everyday life and specialized fields. Remember that the core concept remains consistent: a percentage represents a fraction of 100, and this fundamental understanding underpins all percentage calculations, no matter how complex they may appear.
Latest Posts
Latest Posts
-
Which Phase Do Chromosomes First Become Visible
May 12, 2025
-
Is Salt Water Good For Plants
May 12, 2025
-
A Science Test Which Is Worth 100 Points
May 12, 2025
-
How To Find The Slope Of A Standard Form Equation
May 12, 2025
-
Balanced Equation Of Acetic Acid And Sodium Bicarbonate
May 12, 2025
Related Post
Thank you for visiting our website which covers about 60 Out Of 200 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.