60 Is 25 Of What Number
listenit
May 10, 2025 · 4 min read
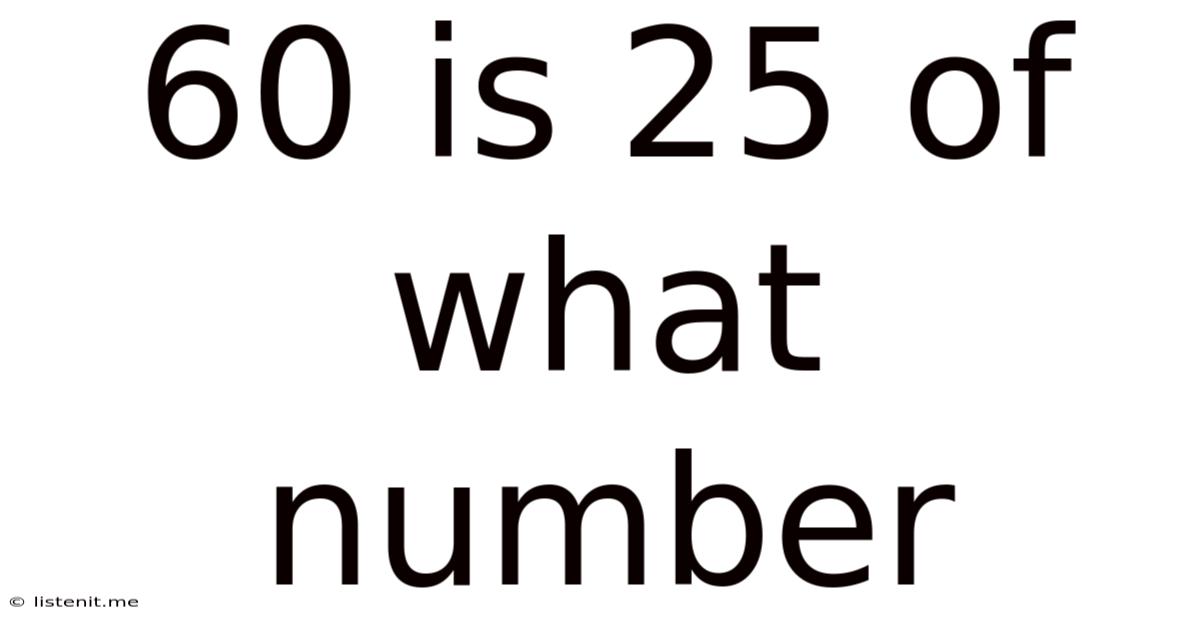
Table of Contents
60 is 25% of What Number? Unraveling Percentage Problems
This article will delve into the question: "60 is 25% of what number?" We'll explore various methods for solving this type of percentage problem, providing a comprehensive understanding that extends beyond a simple answer. We’ll also examine the broader context of percentages, their applications in everyday life, and how to approach similar problems with confidence.
Understanding Percentages
Before diving into the solution, let's solidify our understanding of percentages. A percentage is a fraction expressed as a number out of 100. For instance, 25% means 25 out of 100, or 25/100, which simplifies to 1/4. Understanding this fundamental concept is key to solving percentage problems effectively.
Key Percentage Terminology:
- Percentage: The rate, number, or amount in each hundred.
- Base: The total amount or whole quantity.
- Part: The portion of the base that represents the percentage.
In our problem, "60 is 25% of what number?", we have:
- Part: 60
- Percentage: 25%
- Base: This is what we need to find.
Method 1: Using the Percentage Formula
The most common way to solve percentage problems is using the basic percentage formula:
(Part / Base) * 100 = Percentage
We can rearrange this formula to solve for the base (the unknown number):
Base = (Part / Percentage) * 100
Now, let's plug in the values from our problem:
Base = (60 / 25) * 100
Base = 2.4 * 100
Base = 240
Therefore, 60 is 25% of 240.
Method 2: Using Proportions
Another effective approach is to set up a proportion. A proportion expresses the equality of two ratios. We can represent our problem as:
60 / x = 25 / 100
Where 'x' represents the unknown number (the base). To solve for x, we can cross-multiply:
60 * 100 = 25 * x
6000 = 25x
x = 6000 / 25
x = 240
Again, we find that 60 is 25% of 240.
Method 3: Thinking in Fractions
Since 25% is equivalent to 1/4, we can rephrase the problem as:
60 is 1/4 of what number?
To solve this, we can multiply 60 by the reciprocal of 1/4, which is 4:
60 * 4 = 240
This method offers a simpler, more intuitive approach for percentages that easily convert to simple fractions.
Practical Applications of Percentage Problems
Percentage calculations are ubiquitous in everyday life. Here are some examples:
- Sales and Discounts: Calculating the final price after a percentage discount. For example, a 30% discount on a $100 item.
- Taxes: Determining the amount of tax payable on a purchase or income.
- Tips and Gratuities: Calculating the appropriate tip amount in a restaurant.
- Interest Rates: Understanding interest earned on savings accounts or interest paid on loans.
- Profit Margins: Assessing the profitability of a business by calculating the percentage of profit relative to revenue.
- Statistical Analysis: Representing data and trends using percentages in surveys, polls, and scientific research.
- Financial Reporting: Presenting financial data such as growth rates, expense ratios, and return on investment as percentages.
Solving More Complex Percentage Problems
The techniques discussed above can be extended to solve more complex percentage problems. Let’s consider a few examples:
Example 1: Finding the Percentage:
What percentage of 150 is 30?
Using the formula: (Part / Base) * 100 = Percentage
(30 / 150) * 100 = 20%
Example 2: Finding the Part:
What is 15% of 80?
Using the formula: (Percentage / 100) * Base = Part
(15 / 100) * 80 = 12
Example 3: Consecutive Percentage Changes:
A product is increased by 20% and then decreased by 10%. What is the net percentage change?
This requires a step-by-step approach:
- Increase: 100 + (20% of 100) = 120
- Decrease: 120 - (10% of 120) = 108
- Net Change: 108 - 100 = 8
- Percentage Change: (8 / 100) * 100 = 8% (Net increase of 8%)
Advanced Techniques and Tools
For more complex scenarios involving multiple percentage changes or intricate calculations, consider these options:
- Spreadsheets: Tools like Microsoft Excel or Google Sheets provide built-in functions for percentage calculations, making complex problems easier to manage.
- Calculators: Many calculators have dedicated percentage functions.
- Online Percentage Calculators: Numerous websites offer free online percentage calculators that can handle various types of percentage problems.
Conclusion
Understanding percentages is a fundamental skill with widespread applications. Mastering the techniques outlined in this article, including using the percentage formula, proportions, and fractional equivalents, will equip you to confidently tackle a wide range of percentage problems encountered in daily life, academic studies, and professional settings. Remember to break down complex problems into smaller, manageable steps and utilize available tools to streamline the process. The ability to accurately and efficiently solve percentage problems is a valuable asset in numerous contexts. By applying these methods and practicing regularly, you’ll develop a strong foundation in percentage calculations and improve your overall mathematical proficiency.
Latest Posts
Latest Posts
-
What Is The Conjugate Acid Of H2s
May 10, 2025
-
What Is 1 And 1 2 As An Improper Fraction
May 10, 2025
-
Write The Complete Ground State Electron Configuration Of Barium
May 10, 2025
-
Find The Derivative By Limit Process
May 10, 2025
-
Thickness Of The Outer Core Of The Earth
May 10, 2025
Related Post
Thank you for visiting our website which covers about 60 Is 25 Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.