6 Is What Percentage Of 10
listenit
May 24, 2025 · 5 min read
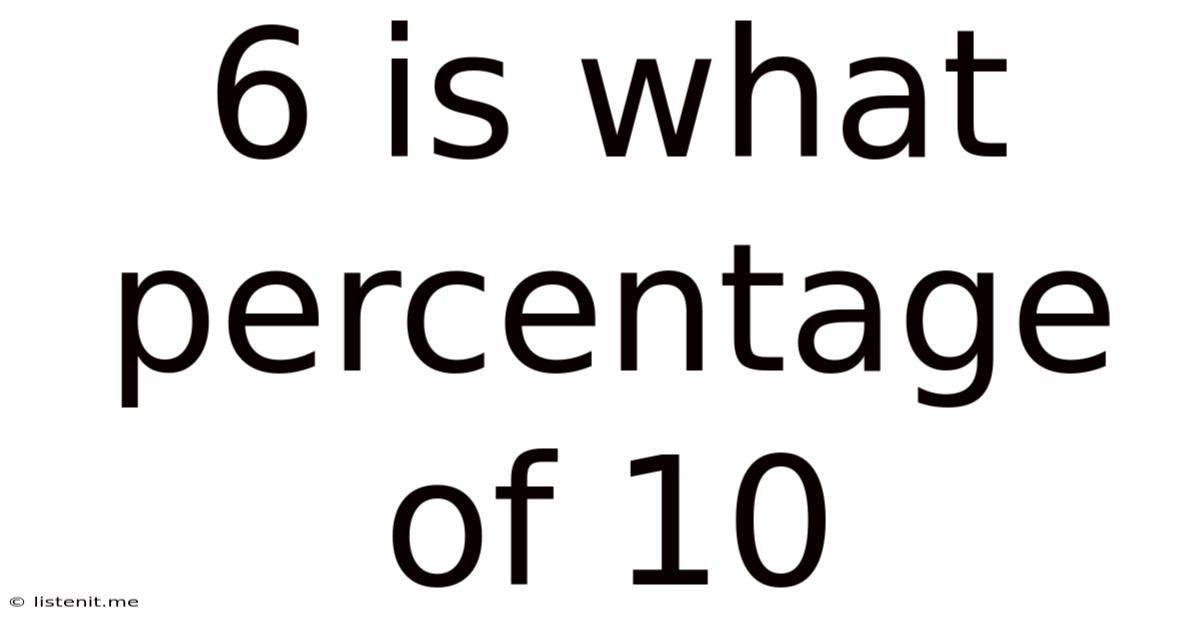
Table of Contents
6 is What Percentage of 10? A Deep Dive into Percentages and Their Applications
Understanding percentages is a fundamental skill in mathematics with broad applications in everyday life, from calculating discounts and taxes to interpreting statistical data and analyzing financial reports. This article will delve into the question, "6 is what percentage of 10?", providing a comprehensive explanation of the calculation, exploring various methods, and showcasing real-world examples to solidify your understanding. We will also explore related percentage calculations and provide tips for mastering this essential mathematical concept.
Understanding the Fundamentals: Percentages and Ratios
Before jumping into the calculation, let's refresh our understanding of percentages and ratios. A percentage represents a fraction of 100. It expresses a proportion of a whole as a number out of 100. The symbol "%" signifies percentage.
A ratio, on the other hand, compares two quantities. It can be expressed as a fraction, a colon (:), or using the word "to." For example, the ratio of 6 to 10 can be written as 6/10, 6:10, or 6 to 10.
Percentages and ratios are intrinsically linked. A percentage can be easily converted into a ratio, and vice versa. The percentage calculation we're about to undertake involves converting a ratio into a percentage.
Calculating "6 is What Percentage of 10?"
The core of the problem lies in determining what percentage 6 represents when compared to the whole, which is 10. We can solve this using several methods:
Method 1: The Proportion Method
This method utilizes the concept of proportion, setting up an equation to solve for the unknown percentage.
-
Step 1: Set up the proportion:
x/100 = 6/10(where 'x' represents the unknown percentage) -
Step 2: Cross-multiply:
10x = 600 -
Step 3: Solve for 'x':
x = 600/10 = 60
Therefore, 6 is 60% of 10.
Method 2: The Decimal Method
This method involves converting the ratio into a decimal and then multiplying by 100 to express it as a percentage.
-
Step 1: Express the ratio as a decimal:
6/10 = 0.6 -
Step 2: Multiply the decimal by 100 to convert it to a percentage:
0.6 * 100 = 60%
Again, we arrive at the answer: 6 is 60% of 10.
Method 3: Using a Calculator
Most calculators have a percentage function. Simply input "6 ÷ 10 =" and then multiply the result by 100. This directly yields the answer: 60%.
Real-World Applications: Putting Percentages to Work
Understanding percentage calculations isn't just about academic exercises; it has immense practical value in various real-world scenarios:
1. Sales and Discounts:
Imagine a store offering a 20% discount on an item originally priced at $50. To calculate the discount amount, you would find 20% of $50, which is ($50 * 0.20 = $10). The discounted price would be $50 - $10 = $40. This scenario uses a similar calculation to our main example, just reversed.
2. Taxes and Tips:
Calculating sales tax or service tips involves percentage calculations. If the sales tax is 6% and the cost of your purchase is $100, you'd calculate the tax amount as ($100 * 0.06 = $6), resulting in a total cost of $106.
3. Financial Investments:
Percentage changes are essential for tracking investment performance. If your investment grows from $100 to $106, the percentage increase is calculated by (6/100) *100% = 6%, demonstrating a 6% return.
4. Statistical Analysis:
Percentages are frequently used in presenting statistical data, such as survey results or demographic information. For example, if 60 out of 100 respondents answered "yes" to a survey question, it's reported as a 60% "yes" response rate.
Expanding on Percentage Calculations: Related Concepts and Techniques
While "6 is what percentage of 10?" provides a simple starting point, several related percentage calculations build upon this foundational understanding:
1. Finding the Whole:
Let's reverse the problem. If 60% of a number is 6, what is the number? To solve this, we set up the equation: 0.6x = 6, where 'x' represents the whole. Solving for 'x', we get x = 6/0.6 = 10.
2. Calculating Percentage Increase or Decrease:
Imagine a quantity increases from 10 to 16. The percentage increase is calculated as: [(16-10)/10] * 100% = 60%. Similarly, a decrease from 10 to 4 would result in a 60% decrease.
3. Compounding Percentages:
When percentages apply successively (e.g., a discount followed by a tax), the calculations are more complex, requiring careful attention to the order of operations.
Mastering Percentages: Tips and Practice
Mastering percentage calculations involves consistent practice and a clear understanding of the underlying concepts. Here are some tips:
-
Practice Regularly: Work through various percentage problems, starting with simple examples and gradually increasing the complexity.
-
Use Different Methods: Familiarize yourself with the various methods (proportion, decimal, calculator) to find the approach best suited to your problem.
-
Understand the Context: Pay close attention to the wording of the problem to correctly identify the whole and the part.
-
Check Your Work: Always double-check your answers using a different method or by estimation.
Conclusion: The Significance of Percentage Calculations
The ability to calculate percentages is a crucial skill with far-reaching implications. From daily financial transactions to complex data analysis, understanding and confidently performing percentage calculations empowers individuals to navigate a wide range of situations effectively. By mastering this fundamental skill, you enhance your ability to make informed decisions, analyze data critically, and confidently solve real-world problems. The seemingly simple question, "6 is what percentage of 10?", serves as a gateway to a much broader and indispensable mathematical concept. The 60% answer is not just a number; it's a key that unlocks a world of practical applications.
Latest Posts
Latest Posts
-
What Is 2 Divided By 7
May 24, 2025
-
15 Months Is How Many Days
May 24, 2025
-
Greatest Common Factor For 12 And 16
May 24, 2025
-
28 Days From October 30 2024
May 24, 2025
-
What Time Is An Hour And A Half From Now
May 24, 2025
Related Post
Thank you for visiting our website which covers about 6 Is What Percentage Of 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.