6 Divided By 1/5 As A Fraction
listenit
May 23, 2025 · 4 min read
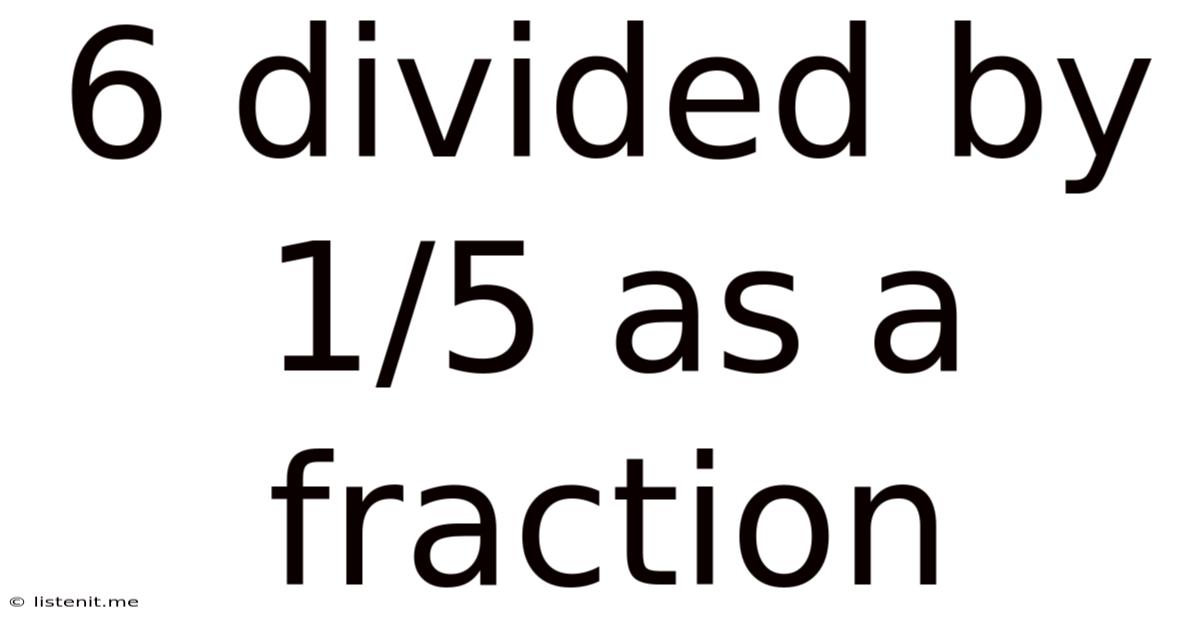
Table of Contents
6 Divided by 1/5 as a Fraction: A Comprehensive Guide
Dividing by fractions can often feel tricky, but with a clear understanding of the underlying principles, it becomes straightforward. This comprehensive guide will delve into the process of calculating 6 divided by 1/5 as a fraction, exploring the fundamental concepts, offering step-by-step solutions, and providing additional examples to solidify your understanding. We'll also touch upon the importance of this skill in various mathematical contexts and real-world applications.
Understanding Fraction Division
Before diving into the specific problem of 6 divided by 1/5, let's revisit the core concept of dividing fractions. The key is to remember that dividing by a fraction is equivalent to multiplying by its reciprocal. The reciprocal of a fraction is simply the fraction flipped upside down – the numerator becomes the denominator, and vice-versa.
For instance, the reciprocal of 1/5 is 5/1 (or simply 5). This fundamental rule simplifies fraction division considerably. Instead of directly dividing by a fraction, we can convert the division problem into a multiplication problem, making the calculation much easier.
The Reciprocal Rule: The Cornerstone of Fraction Division
The reciprocal rule is crucial: a ÷ b/c = a x c/b. This means that dividing 'a' by the fraction 'b/c' is the same as multiplying 'a' by the reciprocal of 'b/c', which is 'c/b'. This rule applies whether 'a' is a whole number, a fraction, or a mixed number.
Solving 6 Divided by 1/5
Now, let's apply this knowledge to solve the problem at hand: 6 divided by 1/5.
Step 1: Express the whole number as a fraction.
It's often easier to work with fractions consistently. We can express the whole number 6 as the fraction 6/1. This doesn't change its value, but it puts it in a format consistent with the other fraction involved in the problem.
Step 2: Find the reciprocal of the divisor.
The divisor is 1/5. Its reciprocal is 5/1, or simply 5.
Step 3: Convert the division problem to a multiplication problem.
Following the reciprocal rule, we change the division problem from:
6/1 ÷ 1/5
to:
6/1 x 5/1
Step 4: Perform the multiplication.
Now, we multiply the numerators together and the denominators together:
(6 x 5) / (1 x 1) = 30/1
Step 5: Simplify the resulting fraction.
30/1 simplifies to 30. Therefore, 6 divided by 1/5 equals 30.
Visualizing the Solution
Imagine you have 6 pizzas, and you want to divide each pizza into fifths (1/5). How many slices of pizza would you have in total? You would have 6 pizzas x 5 slices/pizza = 30 slices. This visual representation helps solidify the understanding of the mathematical process.
Additional Examples and Practice Problems
Let's look at some more examples to reinforce the concept of dividing by fractions:
Example 1: 10 ÷ 1/2
- Express 10 as 10/1.
- The reciprocal of 1/2 is 2/1 (or 2).
- Convert to multiplication: 10/1 x 2/1 = 20/1 = 20
Example 2: 3/4 ÷ 1/8
- The reciprocal of 1/8 is 8/1 (or 8).
- Convert to multiplication: 3/4 x 8/1 = 24/4 = 6
Example 3: 2 1/2 ÷ 1/4
- Convert the mixed number 2 1/2 to an improper fraction: (2 x 2 + 1)/2 = 5/2
- The reciprocal of 1/4 is 4/1 (or 4).
- Convert to multiplication: 5/2 x 4/1 = 20/2 = 10
Practice Problems:
Try these problems to check your understanding:
- 8 ÷ 1/3
- 1/2 ÷ 1/4
- 1 1/3 ÷ 1/6
- 5 ÷ 2/5
- 2/3 ÷ 1/9
Real-World Applications
Understanding fraction division is essential in various real-world scenarios:
- Cooking and Baking: Dividing recipes to accommodate fewer people often involves fraction division.
- Sewing and Tailoring: Calculating fabric requirements frequently necessitates dividing lengths and widths.
- Construction and Engineering: Dividing distances and measurements accurately is critical in various construction tasks.
- Finance and Budgeting: Proportioning budgets and resources involves dividing quantities.
Beyond the Basics: Understanding the "Why"
While the mechanical process of flipping and multiplying is straightforward, understanding the underlying mathematical reasoning provides a deeper appreciation. Dividing by a fraction essentially asks: "How many times does the fraction fit into the whole number (or another fraction)?"
When you divide 6 by 1/5, you are asking: "How many times does 1/5 fit into 6?" The answer, 30, demonstrates that 1/5 fits into 6 thirty times.
Conclusion: Mastering Fraction Division
Mastering fraction division, particularly understanding the reciprocal rule, is a vital skill in mathematics and various real-world applications. By consistently practicing and visualizing the process, you can confidently tackle these problems and build a strong foundation for more advanced mathematical concepts. Remember to always break down the problem into manageable steps, and don't hesitate to use visual aids to solidify your understanding. The ability to confidently divide fractions opens doors to a wider range of mathematical possibilities and problem-solving capabilities.
Latest Posts
Latest Posts
-
Why Is Dlco Increased In Asthma
Jun 05, 2025
-
When To Use A Multiple Regression Analysis
Jun 05, 2025
-
Organisms That Live In The Hadal Zone
Jun 05, 2025
-
How Does The Immune System Work With The Skeletal System
Jun 05, 2025
-
The Present And Future Of Bispecific Antibodies For Cancer Therapy
Jun 05, 2025
Related Post
Thank you for visiting our website which covers about 6 Divided By 1/5 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.