5x 4y 12 In Slope Intercept Form
listenit
May 12, 2025 · 5 min read
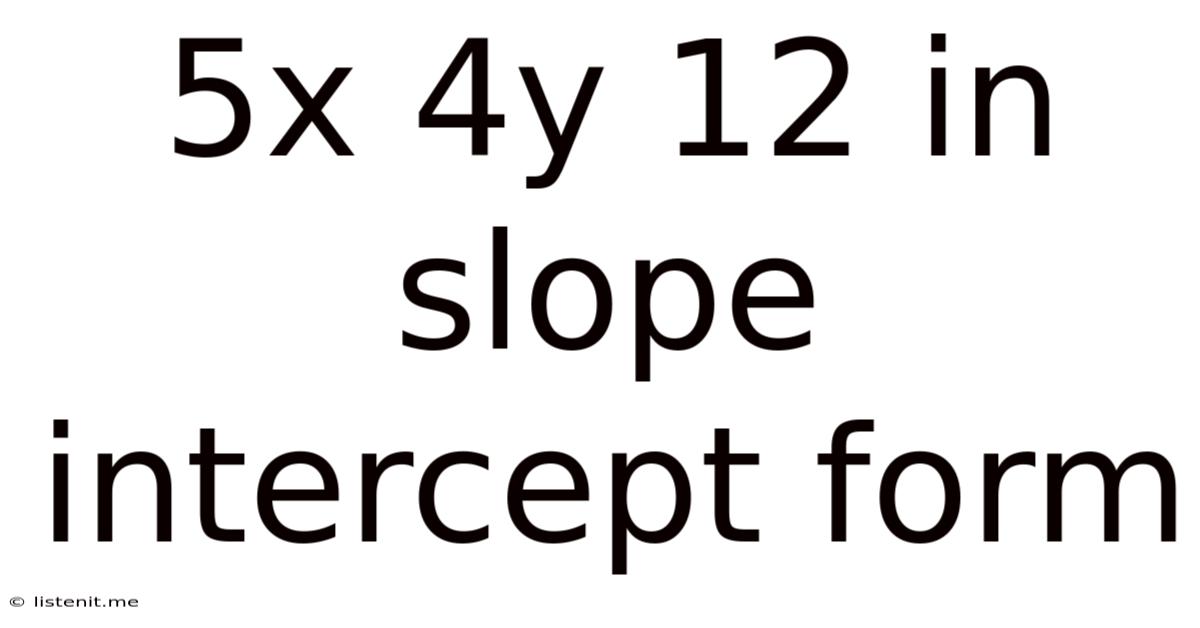
Table of Contents
Converting 5x + 4y = 12 to Slope-Intercept Form: A Comprehensive Guide
The equation 5x + 4y = 12 represents a linear relationship between two variables, x and y. While useful in its current form, converting it to slope-intercept form (y = mx + b) provides valuable insights into the line's characteristics: its slope (m) and y-intercept (b). This guide will walk you through the process step-by-step, explain the significance of the slope and y-intercept, and explore related concepts.
Understanding Slope-Intercept Form (y = mx + b)
Before diving into the conversion, let's review the meaning of each component in the slope-intercept form:
- y: Represents the dependent variable, typically plotted on the vertical axis of a graph.
- m: Represents the slope of the line. The slope indicates the rate of change of y with respect to x. A positive slope means the line ascends from left to right, while a negative slope indicates a descending line. A slope of zero signifies a horizontal line, and an undefined slope represents a vertical line.
- x: Represents the independent variable, usually plotted on the horizontal axis.
- b: Represents the y-intercept, which is the point where the line intersects the y-axis (where x = 0).
Converting 5x + 4y = 12 to Slope-Intercept Form
The goal is to isolate 'y' on one side of the equation. We achieve this through algebraic manipulation:
-
Subtract 5x from both sides:
This step removes the '5x' term from the left side, leaving only the 'y' term:
4y = -5x + 12
-
Divide both sides by 4:
This isolates 'y', giving us the slope-intercept form:
y = (-5/4)x + 3
Therefore, the equation 5x + 4y = 12 in slope-intercept form is y = (-5/4)x + 3.
Interpreting the Slope and Y-intercept
Now that we have the equation in slope-intercept form, we can easily identify the slope and y-intercept:
-
Slope (m) = -5/4: This negative slope indicates that the line slopes downwards from left to right. The magnitude of the slope, 5/4 or 1.25, signifies that for every 4 units of increase in x, y decreases by 5 units.
-
Y-intercept (b) = 3: This means the line crosses the y-axis at the point (0, 3).
Graphing the Line
With the slope and y-intercept, graphing the line becomes straightforward:
-
Plot the y-intercept: Start by plotting the point (0, 3) on the y-axis.
-
Use the slope to find another point: The slope is -5/4. This means we can move 4 units to the right and 5 units down from the y-intercept to find another point on the line: (4, -2).
-
Draw the line: Connect the two points (0, 3) and (4, -2) with a straight line. This line represents the equation 5x + 4y = 12.
Exploring Related Concepts
The conversion to slope-intercept form unlocks several avenues for deeper understanding:
1. Finding the x-intercept:
The x-intercept is the point where the line crosses the x-axis (where y = 0). To find it, set y = 0 in the original equation or the slope-intercept form and solve for x:
0 = (-5/4)x + 3
(5/4)x = 3
x = (4/5) * 3 = 12/5 = 2.4
The x-intercept is (2.4, 0).
2. Parallel and Perpendicular Lines:
-
Parallel Lines: Parallel lines have the same slope. Any line parallel to y = (-5/4)x + 3 will also have a slope of -5/4. The y-intercept can be different.
-
Perpendicular Lines: Perpendicular lines have slopes that are negative reciprocals of each other. The negative reciprocal of -5/4 is 4/5. Any line perpendicular to y = (-5/4)x + 3 will have a slope of 4/5.
3. Applications in Real-World Scenarios:
Linear equations, and their slope-intercept form, have numerous real-world applications. For example:
-
Calculating costs: A linear equation might model the total cost (y) of producing a certain number of items (x), where the slope represents the cost per item and the y-intercept represents fixed costs.
-
Analyzing trends: Linear equations can be used to analyze trends in data, such as population growth or sales figures, where the slope represents the rate of change and the y-intercept represents the starting point.
-
Predicting future values: By extending the line, you can predict future values based on the established trend.
4. Solving Systems of Equations:
The slope-intercept form is particularly useful when solving systems of linear equations graphically. The solution to a system of equations is the point where the lines intersect.
Advanced Concepts and Further Exploration
For those seeking a deeper understanding, consider exploring these advanced topics:
-
Linear Inequalities: Extend your knowledge beyond equations to inequalities, which represent regions on a graph rather than single lines.
-
Matrices and Linear Algebra: Explore how matrices can be used to solve systems of linear equations efficiently.
-
Calculus and Linear Approximation: Learn how linear equations can be used to approximate functions near specific points.
Conclusion
Converting the equation 5x + 4y = 12 to slope-intercept form (y = (-5/4)x + 3) provides a clear and concise representation of the linear relationship between x and y. Understanding the slope and y-intercept allows for easy graphing, identification of parallel and perpendicular lines, and application to real-world scenarios. This comprehensive guide has equipped you with the knowledge to not only perform the conversion but also to deeply understand its implications and applications. Further exploration of the advanced concepts mentioned will solidify your understanding of linear equations and their significance in mathematics and beyond. Remember to practice regularly to master these concepts and build a strong foundation in algebra.
Latest Posts
Related Post
Thank you for visiting our website which covers about 5x 4y 12 In Slope Intercept Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.