5000 Is 30 Percent Of What Number
listenit
May 25, 2025 · 5 min read
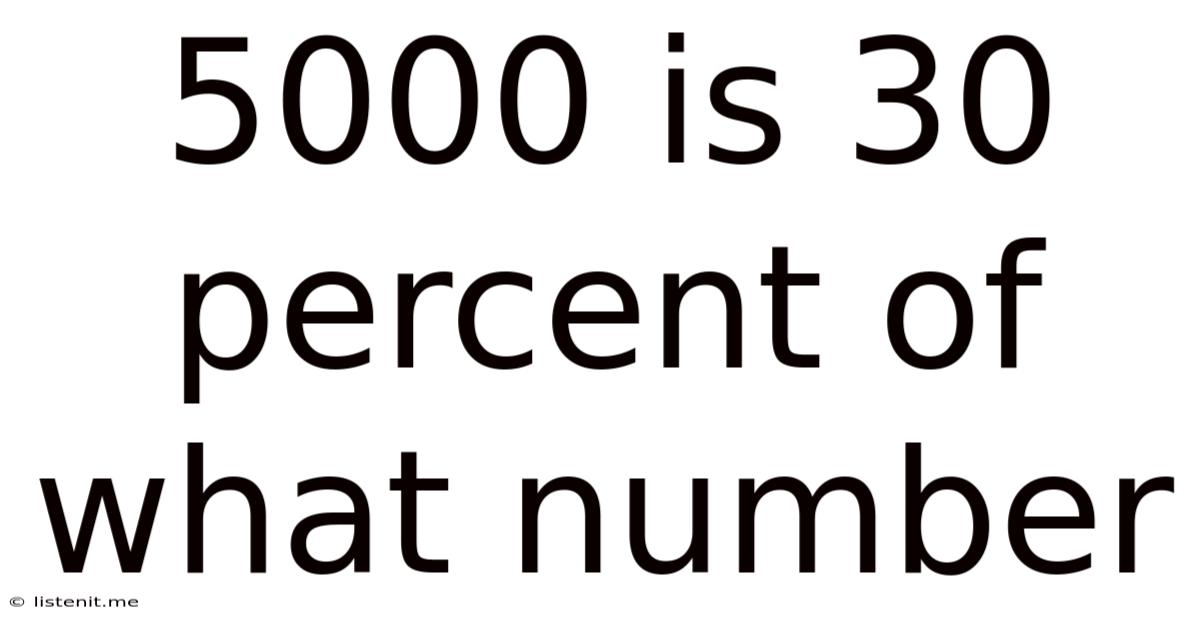
Table of Contents
5000 is 30 Percent of What Number: A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill applicable across various fields, from everyday budgeting to complex financial analysis. Understanding how to solve percentage problems, such as determining the whole when you know a part and its percentage, is crucial for anyone aiming to improve their numerical literacy. This article delves deep into the problem "5000 is 30 percent of what number?", explaining the solution methodically and offering practical applications and extensions to enhance your understanding of percentage calculations.
Understanding the Problem: Deconstructing the Percentage Equation
The core of the problem, "5000 is 30 percent of what number?", lies in understanding the relationship between a part, a whole, and the percentage that represents the part's proportion to the whole. We can express this relationship mathematically using the following equation:
Part = Percentage × Whole
In our problem:
- Part: 5000 (this is the known value representing 30% of the whole)
- Percentage: 30% (or 0.30 as a decimal – we'll primarily use decimals in our calculations for simplicity)
- Whole: This is what we need to find (let's represent it with the variable 'x')
Therefore, the equation becomes:
5000 = 0.30 × x
Solving for the Unknown: Finding the Whole Number
To solve for 'x' (the whole number), we need to isolate it on one side of the equation. We can do this using simple algebraic manipulation:
-
Divide both sides of the equation by 0.30:
5000 / 0.30 = x
-
Calculate the result:
x ≈ 16666.67
Therefore, 5000 is 30% of approximately 16666.67. The slight decimal is due to the nature of the percentage; 30% doesn't divide perfectly into 5000.
Alternative Methods for Solving Percentage Problems
While the algebraic approach is efficient, other methods can be used to solve similar percentage problems. These alternative approaches enhance understanding and provide different perspectives on tackling these calculations:
Method 1: Using Proportions
Proportions offer a visual way to understand the relationship between parts and wholes. We can set up a proportion as follows:
5000 / x = 30 / 100
This states that the ratio of 5000 to the unknown whole (x) is equal to the ratio of 30% (the part) to 100% (the whole). To solve, cross-multiply:
5000 × 100 = 30 × x
500000 = 30x
x = 500000 / 30
x ≈ 16666.67
This method confirms the result obtained through the algebraic approach.
Method 2: Working with Fractions
Percentages can also be expressed as fractions. 30% is equivalent to 30/100, which simplifies to 3/10. The problem can then be framed as:
5000 = (3/10) × x
Multiplying both sides by 10/3 (the reciprocal of 3/10) isolates x:
x = 5000 × (10/3)
x ≈ 16666.67
This fractional method reinforces the understanding of percentage as a ratio.
Practical Applications: Real-World Scenarios
The ability to solve percentage problems like this has widespread applications:
1. Business and Finance
- Profit margins: If a company made a profit of $5000 and this represents 30% of its revenue, calculating the total revenue is crucial for financial analysis.
- Sales targets: If a salesperson achieved 30% of their sales target ($5000), determining the total sales target helps in performance evaluation.
- Investment returns: Understanding the total investment required to generate a specific return (like $5000 representing 30% of the profit) is crucial for investment decisions.
2. Everyday Life
- Discounts: Calculating the original price of an item when a discounted price is known and the discount percentage is given.
- Tip calculations: Determining the total bill amount when a tip is given as a percentage of the pre-tip cost.
- Budgeting: Tracking expenses and calculating the total budget needed when only a percentage of the expenses is known.
Expanding Your Skills: More Complex Percentage Problems
Understanding the fundamental principle behind solving "5000 is 30 percent of what number?" empowers you to tackle more complex percentage problems:
1. Finding Percentage Increase or Decrease
Imagine a scenario where a quantity increases by a certain percentage. For example: A company's sales increased by 30% to reach $5000. To find the original sales figure, you need to adjust the equation:
Let 'x' be the original sales figure. The increased sales are represented by x + 0.30x = 1.30x. Therefore:
1.30x = 5000
x = 5000 / 1.30
x ≈ 3846.15
The original sales were approximately $3846.15.
Similar principles apply when calculating percentage decreases.
2. Multiple Percentage Changes
Problems involving sequential percentage changes require careful step-by-step calculation. For instance, if a quantity increases by 20% and then decreases by 10%, the final result is not simply a 10% increase. You must calculate each change sequentially.
3. Compound Interest
Compound interest calculations rely heavily on percentage calculations. Understanding how interest accumulates over time, compounded at regular intervals, is fundamental in financial planning.
Conclusion: Mastering Percentage Calculations
The ability to solve percentage problems, like finding the whole when a part and its percentage are known, is a valuable skill across numerous domains. By understanding the fundamental equation, mastering algebraic manipulation, and exploring alternative solution methods, you can confidently tackle various percentage problems. The examples provided illustrate the practical applicability of these calculations in everyday life and professional settings. Continuous practice and exploring more complex problems will further solidify your understanding and proficiency in working with percentages. Remember that mastering this skill is not just about finding numerical answers but also about developing a strong conceptual grasp of ratios and proportions. This understanding forms the bedrock for more advanced mathematical and financial concepts.
Latest Posts
Latest Posts
-
1 4 Divided By 3 8 As A Fraction
May 25, 2025
-
What Is Ten Percent Of One Million
May 25, 2025
-
What Is The Greatest Common Factor Of 40 And 30
May 25, 2025
-
What Is The Gcf Of 7 And 12
May 25, 2025
-
What Is 27 Out Of 35 As A Percentage
May 25, 2025
Related Post
Thank you for visiting our website which covers about 5000 Is 30 Percent Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.