50 Is 1/10 Of What Number
listenit
May 25, 2025 · 6 min read
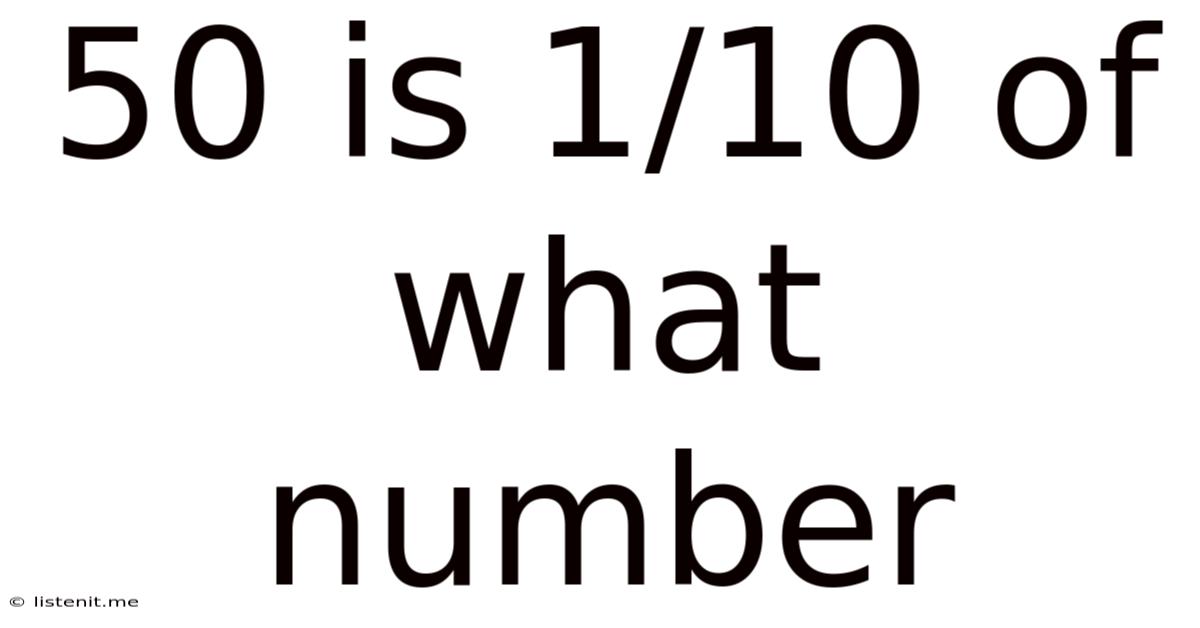
Table of Contents
50 is 1/10 of What Number: A Deep Dive into Fractions and Problem-Solving
This seemingly simple question, "50 is 1/10 of what number?", opens a door to a world of mathematical concepts, problem-solving strategies, and real-world applications. While the answer itself might be quickly apparent to some, understanding the underlying principles and exploring different approaches to solving this type of problem is crucial for building a strong mathematical foundation. This article will not only provide the solution but also delve into the various methods for arriving at the answer, highlighting the importance of fractions and their significance in various fields.
Understanding the Problem: Deconstructing the Question
The question, "50 is 1/10 of what number?", can be rephrased in a more mathematically accessible way: 50 = (1/10) * x, where 'x' represents the unknown number we're trying to find. This equation clearly illustrates the relationship between 50, the fraction 1/10, and the unknown variable 'x'. Understanding this equation is the first step towards solving the problem efficiently.
Method 1: Using Inverse Operations
The most straightforward method involves using inverse operations to isolate the unknown variable, 'x'. Since 'x' is multiplied by 1/10, we can use the inverse operation of multiplication, which is division, to solve for 'x'.
- Step 1: Rewrite the equation: 50 = (1/10) * x
- Step 2: Multiply both sides by the reciprocal of 1/10: The reciprocal of 1/10 is 10/1 or simply 10. Multiplying both sides of the equation by 10 will cancel out the fraction on the right side: 10 * 50 = 10 * (1/10) * x
- Step 3: Simplify: This simplifies to 500 = x.
Therefore, 50 is 1/10 of 500.
Method 2: Utilizing Proportions
Proportions offer another elegant way to solve this problem. A proportion expresses the equality of two ratios. We can set up a proportion as follows:
- Step 1: Set up the proportion: We know that 50 is 1/10 of the unknown number (x). This can be written as a ratio: 50/x = 1/10.
- Step 2: Cross-multiply: Cross-multiplication is a technique used to solve proportions. Multiply the numerator of the first ratio by the denominator of the second ratio, and vice versa: 50 * 10 = 1 * x.
- Step 3: Simplify: This simplifies to 500 = x.
Again, we arrive at the solution: x = 500.
Method 3: Visual Representation using a Fraction Model
Visualizing the problem using a fraction model can be particularly helpful for those who prefer a more intuitive approach. Imagine a whole divided into ten equal parts. Each part represents 1/10 of the whole. If one of these parts (1/10) is equal to 50, then the entire whole (10/10) would be ten times larger: 50 * 10 = 500. This method is excellent for solidifying the understanding of fractions and their representation.
Real-World Applications: Where do we use this concept?
The concept of finding a number when given a fraction of it has extensive real-world applications in various fields:
1. Percentage Calculations:
Percentages are simply fractions expressed as parts of 100. If you know that a certain amount represents a percentage of a total, you can use this method to find the total. For example, if a down payment of $5000 represents 10% of the total cost of a house, you can find the total cost by solving: 5000 = (10/100) * x. This is essentially the same type of problem as the one we've been exploring.
2. Business and Finance:
In finance, calculating profits, losses, interest, and investments frequently involves working with fractions and proportions. For instance, determining the total investment amount when only a fraction of the return is known necessitates this type of problem-solving skill.
3. Scaling and Measurement:
In fields like engineering and architecture, scaling models and blueprints require accurate calculations involving fractions. If a scale model is 1/10 the size of the actual building, and the model is 50cm tall, you can use this method to find the actual height of the building.
4. Data Analysis and Statistics:
Understanding and interpreting data often involves working with fractions and proportions. If a sample represents a certain fraction of the total population, you can use the problem-solving approach discussed to estimate the total population size or other relevant population parameters based on the sample data.
5. Everyday Scenarios:
Even in our daily lives, we encounter scenarios that involve fractions. For example, if you know that you've completed 1/10 of a project and have spent 50 hours, you can calculate the total time required to complete the entire project.
Expanding the Concept: Variations on the Theme
The basic principle of finding a whole number given a fraction of it can be expanded to more complex problems:
-
Different Fractions: The question could involve any fraction, not just 1/10. For example, "50 is 2/5 of what number?" The approach remains the same; you would just use the reciprocal of 2/5 (5/2) to solve the equation.
-
Decimals and Percentages: The fraction can also be expressed as a decimal or a percentage. The approach remains consistent; simply convert the decimal or percentage to a fraction before solving.
-
Word Problems: The problem can be presented in the form of a word problem, requiring a greater understanding of the context and how to translate the words into an equation.
Mastering Fractions: The Key to Success
Proficiency in solving problems like "50 is 1/10 of what number?" hinges on a solid understanding of fractions, including:
-
Reciprocals: Understanding the concept of reciprocals (flipping the numerator and denominator) is essential for using inverse operations effectively.
-
Cross-multiplication: This technique is a powerful tool for solving proportions, a common way to approach fraction-based problems.
-
Fraction Simplification: Simplifying fractions before carrying out calculations helps to avoid errors and make the calculations more manageable.
-
Visual Representation: Using diagrams or models can help to visualize the problem and make it easier to grasp the concept.
Conclusion: Building a Strong Mathematical Foundation
This seemingly simple question about fractions opens up a world of mathematical concepts and problem-solving strategies. Mastering the skills and techniques presented in this article will not only help you solve this specific type of problem but also equip you with the skills to tackle more complex mathematical challenges in various fields. Remember, the key to success lies in understanding the fundamental principles of fractions, practicing different solution methods, and applying these concepts to real-world scenarios. By building a strong mathematical foundation, you'll be better prepared to navigate the complexities of the world around you.
Latest Posts
Latest Posts
-
1 Day 6 Hours From Now
May 25, 2025
-
3 2 4 As An Improper Fraction
May 25, 2025
-
Greatest Common Factor Of 63 And 49
May 25, 2025
-
What Is 6 3 4 As A Decimal
May 25, 2025
-
3050 Divided By 75 With Remainder
May 25, 2025
Related Post
Thank you for visiting our website which covers about 50 Is 1/10 Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.