50 9 As A Mixed Number
listenit
May 24, 2025 · 5 min read
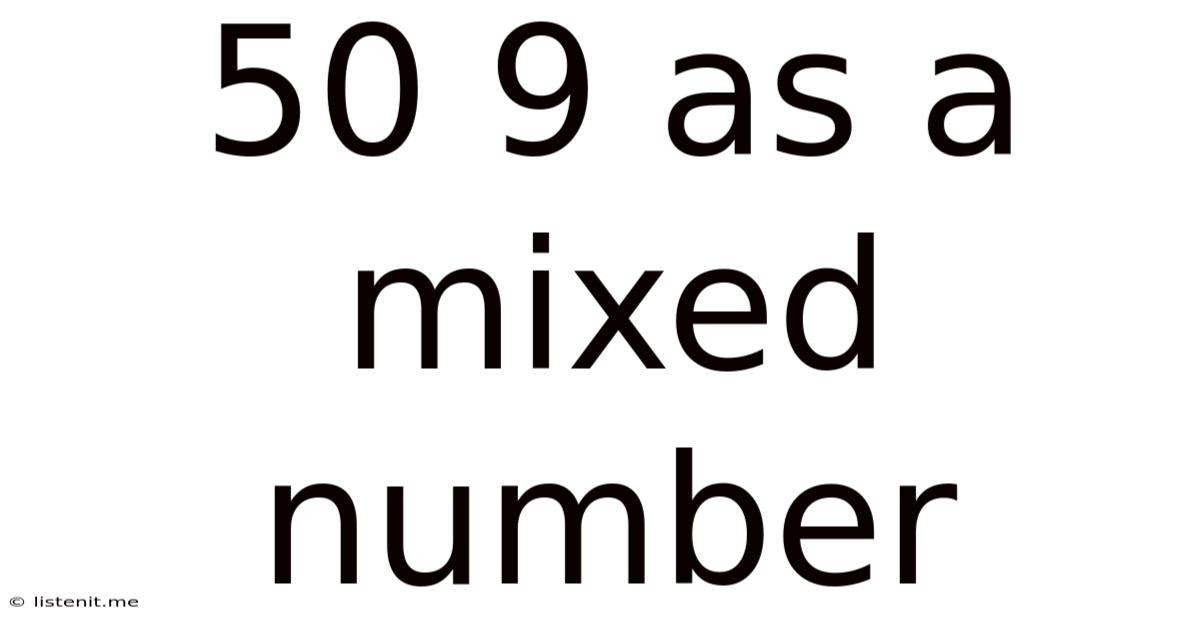
Table of Contents
50/9 as a Mixed Number: A Comprehensive Guide
Understanding how to convert improper fractions, like 50/9, into mixed numbers is a fundamental skill in mathematics. This comprehensive guide will walk you through the process, explaining the concept, providing step-by-step instructions, and exploring various applications. We'll delve deeper than a simple calculation, examining the underlying principles and demonstrating the practical relevance of this conversion.
What is a Mixed Number?
A mixed number combines a whole number and a proper fraction. A proper fraction is a fraction where the numerator (the top number) is smaller than the denominator (the bottom number). For example, 2 ¾ is a mixed number; 2 is the whole number, and ¾ is the proper fraction. Understanding this distinction is crucial for converting improper fractions.
What is an Improper Fraction?
An improper fraction is a fraction where the numerator is greater than or equal to the denominator. 50/9 is an improper fraction because 50 (the numerator) is larger than 9 (the denominator). Improper fractions represent a value greater than or equal to one.
Converting 50/9 to a Mixed Number: The Step-by-Step Process
Converting 50/9 into a mixed number involves dividing the numerator by the denominator. Here's how:
- Divide the Numerator by the Denominator: Divide 50 by 9.
9 | 50 -45 5 - Identify the Whole Number: The quotient (the result of the division) is 5. This becomes the whole number part of your mixed number.
- Identify the Remainder: The remainder is 5. This becomes the numerator of the fractional part of your mixed number.
- Keep the Original Denominator: The denominator remains the same (9).
- Combine the Whole Number and Fraction: The mixed number is 5 ⁵/₉.
Therefore, 50/9 as a mixed number is 5 ⁵/₉.
Understanding the Conversion: Why it Works
The conversion process works because it essentially separates the whole numbers from the fractional part of the improper fraction. When you divide 50 by 9, you're finding out how many times 9 fits completely into 50. It fits 5 times (the whole number). The remainder (5) represents the portion of 9 that's left over, forming the proper fraction ⁵/₉.
Practical Applications of Converting Improper Fractions to Mixed Numbers
Converting improper fractions to mixed numbers is not just a theoretical exercise; it has significant practical applications in various fields:
-
Measurement: Imagine you have 50 inches of ribbon and need to cut it into pieces that are 9 inches long. Converting 50/9 to 5 ⁵/₉ tells you that you can cut 5 complete pieces, with ⁵/₉ of an inch left over.
-
Cooking and Baking: Recipes often call for fractional amounts of ingredients. If a recipe requires 50/9 cups of flour, converting it to 5 ⁵/₉ cups makes it easier to measure using standard measuring cups.
-
Construction and Engineering: Precise measurements are critical in construction and engineering. Converting improper fractions to mixed numbers provides a clearer and more practical representation of dimensions and quantities.
-
Data Analysis: When working with data involving fractions, converting improper fractions to mixed numbers can improve readability and interpretation, especially when presenting data in reports or visualizations.
-
Everyday Life: Many everyday situations involve fractions, from sharing food to calculating distances. Understanding how to convert improper fractions to mixed numbers improves your ability to handle these situations efficiently and accurately.
Beyond the Basics: Working with Mixed Numbers
Once you've converted an improper fraction to a mixed number, you can perform various arithmetic operations. Here are a few examples:
-
Addition and Subtraction: To add or subtract mixed numbers, you typically convert them back into improper fractions to simplify the process. For example, adding 5 ⁵/₉ + 2 ¼ would involve converting both mixed numbers into improper fractions (50/9 + 9/4) and then finding a common denominator before adding.
-
Multiplication and Division: Multiplying and dividing mixed numbers also often involves converting them into improper fractions first for easier calculation.
Common Mistakes to Avoid
When converting improper fractions to mixed numbers, be mindful of these common mistakes:
-
Incorrect Division: Double-check your division to ensure accuracy. A small error in division can lead to an incorrect mixed number.
-
Forgetting the Remainder: Remember that the remainder becomes the numerator of the proper fraction in the mixed number.
-
Using the Wrong Denominator: Always keep the original denominator of the improper fraction as the denominator in the mixed number.
-
Not Simplifying the Fraction: If the resulting proper fraction can be simplified, remember to do so. For example, if you had obtained 6 ⁶/₁₂, you should simplify the fraction to 6 ¹/₂.
Practice Makes Perfect
The best way to master converting improper fractions to mixed numbers is through practice. Try converting different improper fractions to mixed numbers. Start with simpler examples and gradually move to more complex ones. Online resources and math workbooks offer ample practice problems.
Conclusion: Mastering a Fundamental Skill
Converting an improper fraction like 50/9 to a mixed number (5 ⁵/₉) is a fundamental skill with broad applications in numerous aspects of life. This guide provided a thorough understanding of the process, highlighting its practical importance and common pitfalls. Remember that consistent practice is key to mastering this skill and expanding your mathematical abilities. By understanding the underlying principles, you'll not only be able to perform this conversion accurately but also appreciate its significance in various practical contexts. So, grab your pencil and paper, and start practicing! You'll be surprised how quickly you become proficient in converting improper fractions to their mixed number equivalents.
Latest Posts
Latest Posts
-
How Much Taxes On 401k Withdrawal Calculator
May 24, 2025
-
30 Days From January 16th 2024
May 24, 2025
-
How To Calculate 5 Of A Number
May 24, 2025
-
How To Maximize Employer 401k Match Calculator
May 24, 2025
-
What Type Of Triangle Is Shown Below
May 24, 2025
Related Post
Thank you for visiting our website which covers about 50 9 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.