5 Root 2 + Root 2
listenit
May 09, 2025 · 5 min read
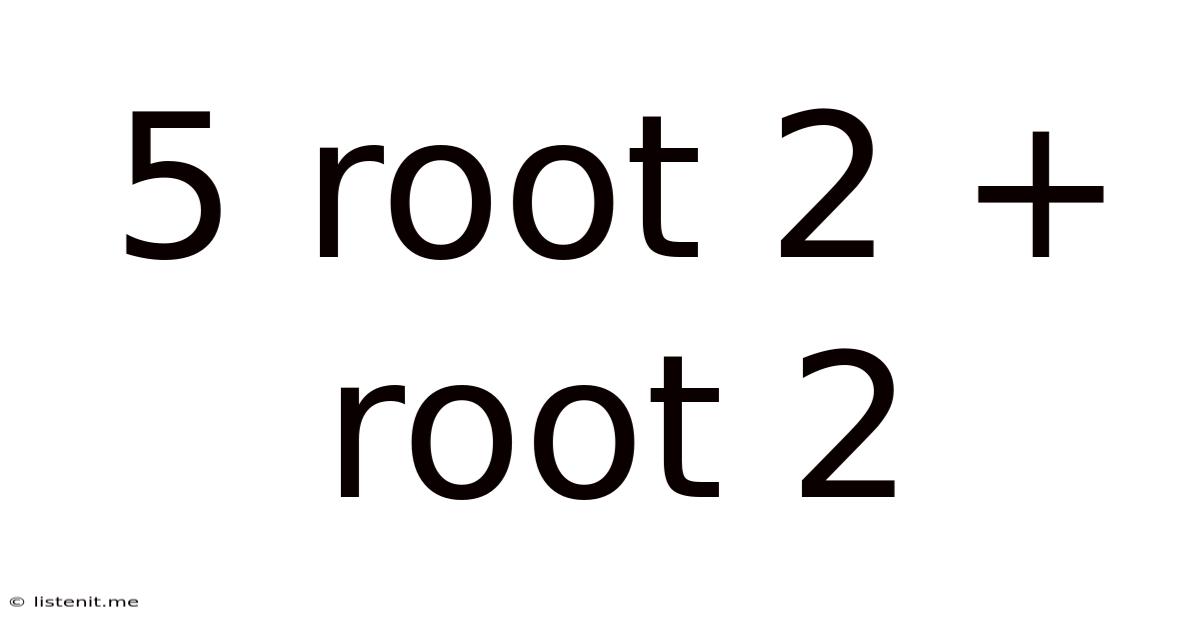
Table of Contents
5√2 + √2: A Deep Dive into Simplifying Surds
The seemingly simple expression, 5√2 + √2, offers a gateway to understanding fundamental concepts in mathematics, specifically concerning surds and their simplification. While the answer might seem immediately obvious to some, a thorough exploration reveals underlying principles applicable to more complex algebraic manipulations. This article will dissect this expression, exploring its simplification, the underlying principles of surd manipulation, and its applications in various mathematical contexts.
Understanding Surds
Before diving into the simplification of 5√2 + √2, let's establish a solid understanding of surds. A surd, also known as a radical, is an irrational number expressed as the root of an integer that cannot be simplified to a rational number. In simpler terms, it's a number that cannot be expressed as a simple fraction. √2, √3, √5 are all examples of surds. They represent irrational numbers; their decimal expansions are infinite and non-repeating.
Key Properties of Surds
Several key properties govern the manipulation of surds. These include:
-
Addition and Subtraction: Surds can be added or subtracted only if they have the same radicand (the number under the square root symbol). For example, 5√2 + 2√2 = 7√2, but 5√2 + 2√3 cannot be simplified further.
-
Multiplication and Division: Surds can be multiplied and divided, even if their radicands are different. For example, √2 * √3 = √6, and √6 / √2 = √3.
-
Rationalization: Rationalizing the denominator involves removing surds from the denominator of a fraction. This is achieved by multiplying both the numerator and the denominator by the conjugate of the denominator. For example, to rationalize 1/√2, we multiply both the numerator and the denominator by √2, resulting in √2/2.
-
Simplification: Surds can often be simplified by factoring the radicand. For example, √12 can be simplified to 2√3 because 12 = 4 * 3, and √4 = 2.
Simplifying 5√2 + √2
Now, let's return to our original expression: 5√2 + √2. This is a straightforward example of surd addition. Since both terms have the same radicand (√2), we can directly add their coefficients. Think of it like adding apples: 5 apples + 1 apple = 6 apples. Similarly:
5√2 + √2 = (5 + 1)√2 = 6√2
The simplified form of 5√2 + √2 is 6√2. This demonstrates the fundamental principle of combining like terms in algebraic expressions, even when those terms involve surds.
Expanding the Concept: More Complex Surd Expressions
While 5√2 + √2 is relatively simple, the same principles apply to more complex expressions. Let's consider a few examples:
-
3√5 + 7√5 - 2√5: In this case, we have three terms with the same radicand (√5). We can add and subtract the coefficients: (3 + 7 - 2)√5 = 8√5.
-
2√3 + √12: Here, we need to simplify √12 first. Since 12 = 4 * 3, √12 = √(4 * 3) = 2√3. Therefore, 2√3 + √12 = 2√3 + 2√3 = 4√3.
-
√18 + √8 - √2: We simplify each term individually. √18 = √(9 * 2) = 3√2, √8 = √(4 * 2) = 2√2. Therefore, √18 + √8 - √2 = 3√2 + 2√2 - √2 = 4√2.
These examples highlight the importance of simplifying individual surd terms before attempting addition or subtraction. Always look for opportunities to simplify the radicand by factoring out perfect squares.
Applications of Surds
Surds, seemingly abstract mathematical entities, find practical applications in various fields:
-
Geometry: Surds frequently appear in geometric calculations, especially when dealing with triangles and circles. For example, the diagonal of a square with side length 1 is √2. The calculation of areas and volumes often involves surds.
-
Trigonometry: Trigonometric functions often yield surd results, particularly when dealing with special angles like 30°, 45°, and 60°. Solving trigonometric equations frequently leads to expressions involving surds.
-
Physics: Many physical formulas and calculations involve surds, often stemming from the application of Pythagorean theorem or other geometric relationships. Examples include calculations related to velocity, acceleration, and energy.
-
Engineering: In various branches of engineering, such as civil and mechanical engineering, calculations involving surds are commonplace, particularly in structural analysis and design.
-
Computer Graphics: Surds are fundamental in computer graphics and game development for calculations related to vectors, rotations, and transformations.
Advanced Concepts Related to Surds
The simplification of 5√2 + √2 opens doors to a deeper understanding of more advanced concepts:
-
Complex Numbers: Surds can be components of complex numbers, numbers that involve the imaginary unit 'i' (√-1). Operations with complex numbers build upon the principles of surd manipulation.
-
Polynomial Equations: Solving polynomial equations often leads to solutions expressed as surds.
-
Calculus: Surds appear in various calculus problems, especially in integration and differentiation.
Conclusion: The Significance of Mastering Surd Simplification
The seemingly trivial simplification of 5√2 + √2 underscores the importance of mastering surd manipulation. This fundamental skill forms a building block for more complex mathematical operations. Understanding surd properties, simplification techniques, and their applications across various disciplines enhances mathematical proficiency and problem-solving abilities. The ability to simplify surd expressions efficiently and accurately is crucial for success in higher-level mathematics and related fields. Regular practice and a solid grasp of the underlying principles are key to achieving proficiency in this area of mathematics. By mastering these fundamental concepts, one can confidently approach more challenging mathematical problems and appreciate the elegance and power of mathematical simplification. The journey from 5√2 + √2 to a deeper understanding of surds demonstrates the beauty of mathematics and its pervasive role in understanding our world.
Latest Posts
Latest Posts
-
Temperature At Which A Solid Becomes A Liquid
May 09, 2025
-
What Is 0 25 As A Fraction In Simplest Form
May 09, 2025
-
What Do Squares And Rhombuses Have In Common
May 09, 2025
-
Is Sugar Organic Or Inorganic Compound
May 09, 2025
-
16 2 3 As A Decimal
May 09, 2025
Related Post
Thank you for visiting our website which covers about 5 Root 2 + Root 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.