5 Less Than A Number Is 15
listenit
May 10, 2025 · 5 min read
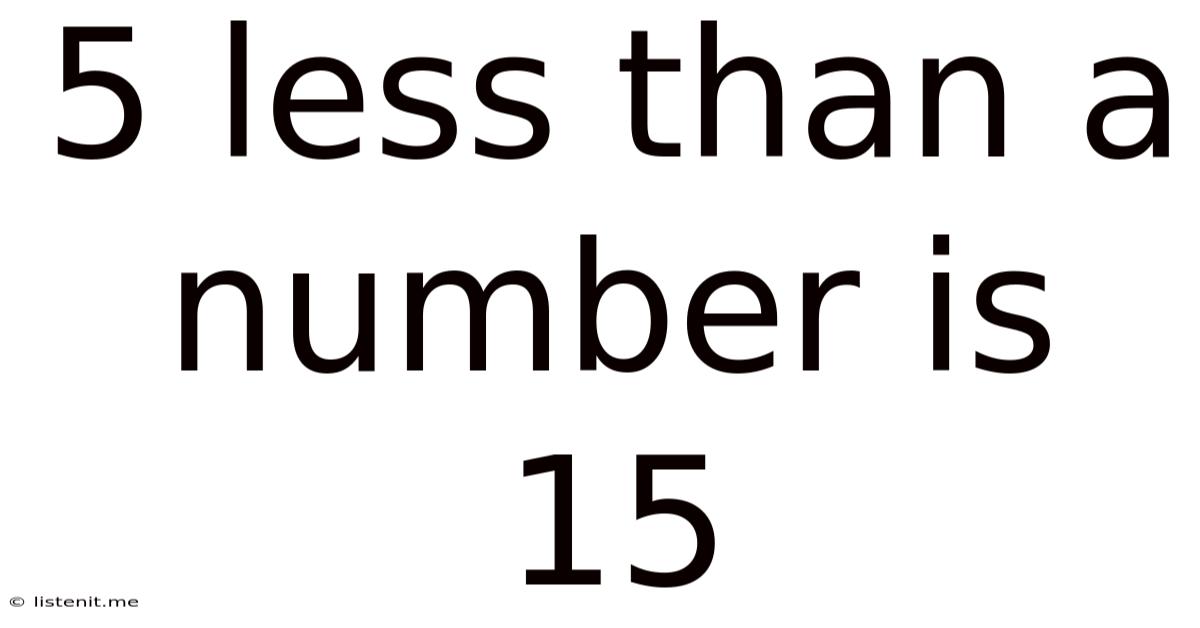
Table of Contents
5 Less Than a Number is 15: Unpacking the Problem and Exploring Related Concepts
This seemingly simple mathematical statement, "5 less than a number is 15," opens a door to a fascinating exploration of algebra, problem-solving techniques, and the underlying principles of mathematical representation. While the solution itself is straightforward, the process of reaching that solution, and the broader mathematical context it sits within, offer valuable insights for students and enthusiasts alike. This article will delve deep into this statement, examining various approaches to solving it and exploring related mathematical concepts.
Understanding the Problem: Translating Words into Equations
The core challenge lies in translating the verbal description into a mathematical equation. The phrase "5 less than a number" immediately suggests subtraction. We don't know the number, so we represent it with a variable, typically 'x'. Therefore, "5 less than a number" translates to x - 5. The phrase "is 15" signifies equality, giving us the complete equation:
x - 5 = 15
This seemingly simple equation encapsulates the essence of algebraic thinking: using symbols to represent unknown quantities and relationships. This ability to translate verbal problems into mathematical notation is a fundamental skill in mathematics and its applications in various fields, including science, engineering, and finance.
Solving the Equation: Unveiling the Unknown
Solving the equation x - 5 = 15 involves isolating the variable 'x' to find its value. This is achieved through the application of inverse operations. Since 5 is subtracted from x, we add 5 to both sides of the equation to maintain balance:
x - 5 + 5 = 15 + 5
This simplifies to:
x = 20
Therefore, the number is 20. We can verify this solution by substituting 20 back into the original equation: 20 - 5 = 15, which is true. This verification step is crucial in mathematics to ensure accuracy and build confidence in the solution.
Alternative Approaches: Exploring Different Paths to the Solution
While the method above is the most straightforward, several alternative approaches can lead to the same solution. These alternative methods not only reinforce the understanding of the problem but also highlight the flexibility and interconnectedness of mathematical concepts.
1. Using a Number Line: A Visual Representation
A number line provides a visual approach to solving the problem. Start at 15 on the number line. Since the number is 5 less than 15, move 5 units to the right (because we're looking for a number larger than 15). This will lead you to 20, visually confirming the solution. This method is particularly useful for introducing algebraic concepts to younger learners, providing a concrete and intuitive understanding of the problem.
2. Working Backwards: Reversing the Operation
Instead of directly solving the equation, we can work backwards from the result. We know that 5 less than a number is 15. To find the number, we simply reverse the subtraction by adding 5: 15 + 5 = 20. This method showcases the inverse relationship between addition and subtraction, a fundamental concept in arithmetic and algebra.
Expanding the Scope: Generalizing the Problem
The problem "5 less than a number is 15" can be generalized to a broader class of problems. We can represent this generalized form as:
x - a = b
where 'x' is the unknown number, 'a' is the number subtracted from x, and 'b' is the result. To solve this generalized equation, we add 'a' to both sides:
x - a + a = b + a
x = b + a
This generalized solution allows us to solve similar problems with different values of 'a' and 'b' without having to rework the entire process each time. This showcases the power of algebra in providing efficient and generalizable solutions to a wide range of problems.
Real-World Applications: Connecting Math to Everyday Life
While seemingly abstract, the concept of solving equations like "5 less than a number is 15" has numerous real-world applications. Consider these examples:
-
Inventory Management: A store has 15 items left after selling 5. How many items were initially in stock? (Solution: 15 + 5 = 20)
-
Financial Calculations: A person has $15 left after spending $5. How much money did they start with? (Solution: 15 + 5 = 20)
-
Temperature Changes: The temperature dropped 5 degrees to reach 15 degrees. What was the initial temperature? (Solution: 15 + 5 = 20)
These examples demonstrate how simple algebraic equations can model real-world scenarios, highlighting the practical relevance of mathematical concepts.
Further Exploration: Expanding Mathematical Horizons
Understanding the solution to "5 less than a number is 15" paves the way for exploring more complex mathematical concepts. This includes:
-
Inequalities: Instead of an equation, we could explore inequalities, such as "5 less than a number is greater than 15". This introduces the concept of ranges of solutions.
-
Simultaneous Equations: We could introduce a second equation involving the same variable, leading to the need to solve simultaneous equations.
-
Quadratic Equations: Moving beyond linear equations, we can explore quadratic equations, introducing more complex problem-solving techniques.
-
Word Problems: Practicing with a variety of word problems helps develop crucial problem-solving skills and enhances the ability to translate real-world situations into mathematical expressions. This is vital for building a strong foundation in mathematics and its applications.
Conclusion: The Enduring Significance of a Simple Equation
The seemingly simple problem "5 less than a number is 15" offers a gateway to a rich tapestry of mathematical concepts and problem-solving techniques. From translating words into equations to employing various solution methods and exploring real-world applications, this problem serves as a powerful illustration of the interconnectedness and practicality of mathematics. By understanding the underlying principles and expanding upon this foundational concept, students can build a robust mathematical foundation that will serve them well in their academic pursuits and beyond. The ability to translate verbal descriptions into mathematical expressions, solve equations, and verify solutions are essential skills not only in mathematics but also across various disciplines, demonstrating the enduring significance of this seemingly simple equation. The journey from a simple statement to a deep understanding of algebraic principles highlights the beauty and power of mathematical thinking.
Latest Posts
Latest Posts
-
Ionic Bond Vs Polar Covalent Bond
May 11, 2025
-
A Pure Substance Made Of Only One Atom
May 11, 2025
-
Does Red Blood Cells Have Organelles
May 11, 2025
-
What Is The Electron Configuration Of Be
May 11, 2025
-
Explain Why Dna Replication Is A Semi Conservative Process
May 11, 2025
Related Post
Thank you for visiting our website which covers about 5 Less Than A Number Is 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.