5 Divided By 1/2 As A Fraction
listenit
May 24, 2025 · 5 min read
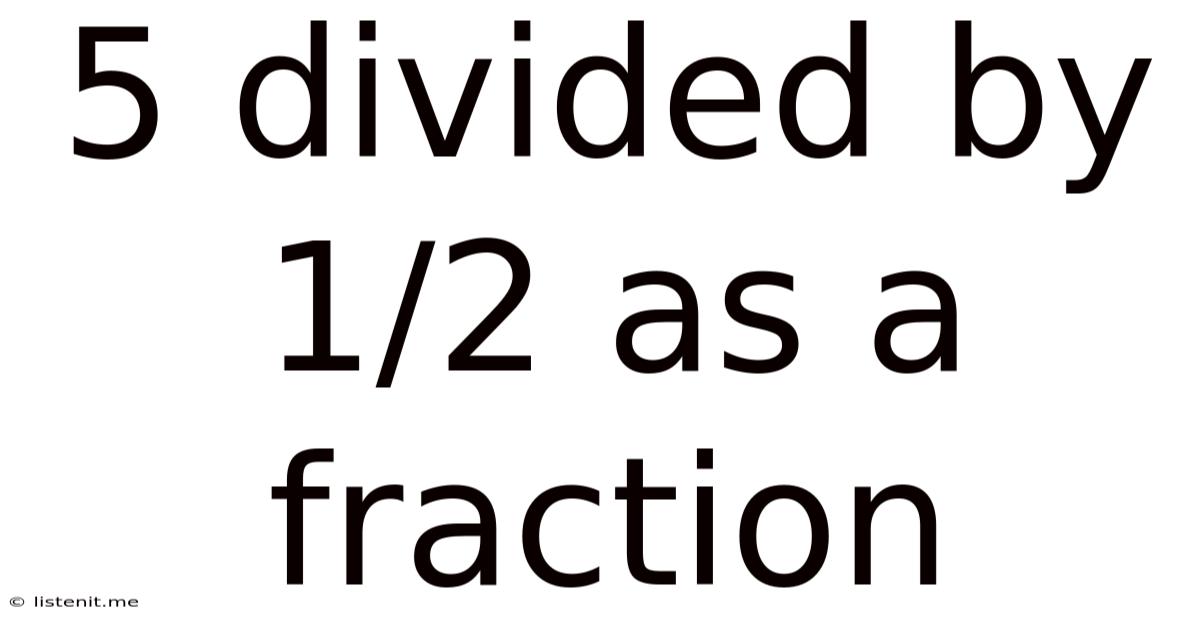
Table of Contents
5 Divided by 1/2 as a Fraction: A Deep Dive into Fraction Division
Understanding fraction division can be tricky, but it's a fundamental concept in mathematics with wide-ranging applications. This article delves into the seemingly simple problem of 5 divided by 1/2, explaining the process in detail, exploring various approaches, and highlighting the underlying mathematical principles. We'll move beyond just finding the answer to truly understanding why the answer is what it is.
Understanding the Problem: 5 ÷ (1/2)
The question, "What is 5 divided by 1/2?", asks how many times the fraction 1/2 fits into the whole number 5. This is a crucial framing of the problem that helps visualize the solution. Imagine you have 5 pizzas, and you want to divide each pizza into halves (1/2). How many half-pizzas do you have in total? This visual representation helps contextualize the mathematical operation.
Method 1: The "Keep, Change, Flip" Method (Inversion)
This is arguably the most common and readily accessible method for dividing fractions. It's a shortcut derived from a more fundamental mathematical principle involving reciprocals. Here's how it works:
1. Keep: Keep the first number (the dividend) as it is. In our case, this remains 5.
2. Change: Change the division sign (÷) to a multiplication sign (×).
3. Flip: Flip the second number (the divisor), which is the fraction 1/2. Flipping a fraction means finding its reciprocal. The reciprocal of 1/2 is 2/1 (or simply 2).
Therefore, the problem becomes: 5 × 2
4. Solve: Multiply the numbers: 5 × 2 = 10
Therefore, 5 divided by 1/2 is 10.
This method offers a quick and efficient way to solve the problem, but let's explore why it works.
Method 2: Understanding Reciprocals and the Mathematical Principle
The "keep, change, flip" method is a simplification of a more profound mathematical concept: reciprocals. The reciprocal of a number is what you multiply it by to get 1. For example, the reciprocal of 3 is 1/3 (because 3 × 1/3 = 1), and the reciprocal of 1/2 is 2 (because 1/2 × 2 = 1).
Dividing by a number is the same as multiplying by its reciprocal. This is a crucial mathematical identity that underpins the "keep, change, flip" method. So, dividing by 1/2 is equivalent to multiplying by its reciprocal, which is 2. Hence, 5 ÷ (1/2) = 5 × 2 = 10.
Method 3: Visual Representation and Real-World Application
Let's solidify our understanding with a visual representation. Imagine you have 5 whole pies. Dividing by 1/2 means cutting each pie into two halves. This results in 10 half-pies (or 10 pieces).
This approach translates easily into real-world scenarios:
- Baking: If a recipe calls for 5 cups of flour, and you only have 1/2 cup measuring cups, you'll need to use the 1/2 cup measuring cup 10 times to get the required amount.
- Construction: If a project requires 5 meters of rope, and you only have 1/2-meter sections, you'll need 10 sections.
- Sharing: If you have 5 candies and want to give each person 1/2 a candy, you can share them with 10 people.
These everyday examples demonstrate the practical application of this seemingly abstract mathematical concept.
Method 4: Converting to Improper Fractions
While the previous methods are efficient, converting to improper fractions offers a more formal, step-by-step approach, reinforcing the principles of fraction arithmetic.
1. Convert the whole number to a fraction: Represent 5 as an improper fraction with a denominator of 1: 5/1.
2. Rewrite the division as a multiplication of reciprocals: Instead of 5/1 ÷ 1/2, write it as 5/1 × 2/1.
3. Multiply the numerators and denominators: (5 × 2) / (1 × 1) = 10/1.
4. Simplify: 10/1 simplifies to 10.
Therefore, 5 divided by 1/2 is 10.
This method emphasizes the rules of fraction multiplication and showcases the equivalence between whole numbers and fractions with a denominator of 1.
Addressing Common Misconceptions
A common mistake is to simply divide 5 by 1 and then by 2, resulting in an incorrect answer of 2.5. This stems from a misunderstanding of how division with fractions works. Remember, dividing by a fraction is essentially multiplying by its reciprocal.
Another misconception involves the order of operations. The problem is specifically 5 divided by 1/2, not 5 divided by 1 and then divided by 2. The parentheses (or the implied grouping) are crucial.
Expanding on Fraction Division: More Complex Examples
The principles illustrated with 5 ÷ (1/2) can be extended to more complex fraction division problems. For example:
-
7 ÷ (2/3): Using the "keep, change, flip" method, this becomes 7 × (3/2) = 21/2 = 10.5.
-
(3/4) ÷ (1/8): This becomes (3/4) × (8/1) = 24/4 = 6.
-
(5/6) ÷ (2/3): This becomes (5/6) × (3/2) = 15/12 = 5/4 = 1.25
In each case, the core principle remains the same: dividing by a fraction is equivalent to multiplying by its reciprocal.
Conclusion: Mastering Fraction Division
Understanding 5 divided by 1/2, and fraction division in general, is crucial for mathematical proficiency. By grasping the underlying principles of reciprocals and applying the "keep, change, flip" method or the conversion to improper fractions, one can confidently tackle various fraction division problems. Remember to visualize the problem, relate it to real-world scenarios, and practice regularly to solidify your understanding. This fundamental skill will serve you well in further mathematical pursuits and various practical applications.
Latest Posts
Latest Posts
-
How Many Days Away Is May 24
May 24, 2025
-
How Many Years Ago Was 1968
May 24, 2025
-
What Is 15 Of An Hour
May 24, 2025
-
Round 99089 186735 To The Nearest Ten
May 24, 2025
-
What Is The Gcf Of 18 And 54
May 24, 2025
Related Post
Thank you for visiting our website which covers about 5 Divided By 1/2 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.