5/8 Divided By 2 As A Fraction
listenit
May 11, 2025 · 4 min read
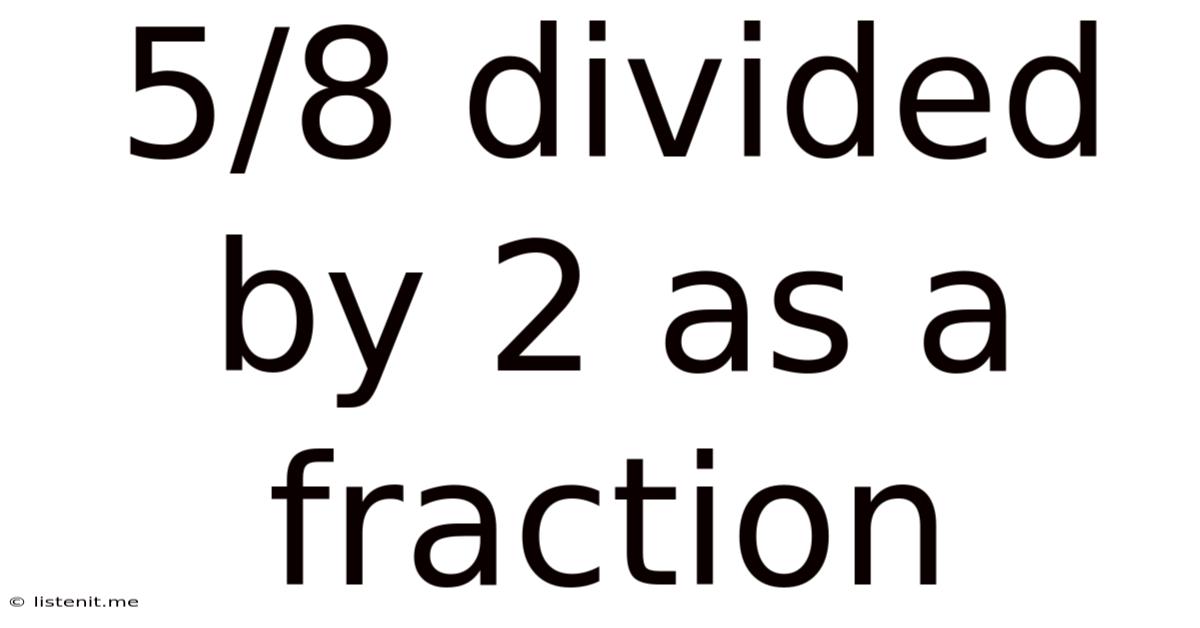
Table of Contents
5/8 Divided by 2: A Comprehensive Guide to Fraction Division
Understanding fraction division is a cornerstone of mathematical proficiency. While it might seem daunting at first, mastering this concept opens doors to more complex mathematical operations and problem-solving. This comprehensive guide will delve into the process of dividing 5/8 by 2, explaining the steps involved and exploring the underlying principles. We'll also cover several related concepts and examples to solidify your understanding.
Understanding Fraction Division
Before tackling the specific problem of 5/8 divided by 2, let's refresh our understanding of fraction division in general. Dividing by a fraction is essentially the same as multiplying by its reciprocal. The reciprocal of a fraction is simply the fraction flipped upside down. For instance, the reciprocal of 2/3 is 3/2.
Key Concept: Dividing by a whole number is the same as multiplying by its reciprocal (1 over that number).
Therefore, dividing 5/8 by 2 is equivalent to multiplying 5/8 by 1/2.
Calculating 5/8 Divided by 2
Now, let's break down the calculation step-by-step:
-
Rewrite the problem as a multiplication: 5/8 ÷ 2 = 5/8 x 1/2
-
Multiply the numerators: Multiply the top numbers (numerators) together: 5 x 1 = 5
-
Multiply the denominators: Multiply the bottom numbers (denominators) together: 8 x 2 = 16
-
Simplify the fraction (if possible): The resulting fraction is 5/16. In this case, 5 and 16 share no common factors other than 1, so the fraction is already in its simplest form.
Therefore, 5/8 divided by 2 is equal to 5/16.
Visualizing Fraction Division
Visual representations can greatly enhance understanding. Imagine you have a pizza cut into 8 slices. You have 5 of those slices (5/8 of the pizza). If you want to divide those 5 slices equally between 2 people, each person will receive 5/16 of the pizza. This visual analogy helps to solidify the abstract concept of fraction division.
Expanding on Fraction Division: Different Scenarios
Let's explore a few variations to broaden our understanding of fraction division.
Dividing a Fraction by Another Fraction
Consider dividing 2/3 by 1/4. The steps remain consistent:
-
Rewrite as multiplication: 2/3 ÷ 1/4 = 2/3 x 4/1
-
Multiply numerators: 2 x 4 = 8
-
Multiply denominators: 3 x 1 = 3
-
Simplify: 8/3 (This is an improper fraction, which can be converted to a mixed number: 2 2/3)
Therefore, 2/3 divided by 1/4 is equal to 8/3 or 2 2/3.
Dividing a Mixed Number by a Fraction
Dividing a mixed number by a fraction requires an extra step: converting the mixed number into an improper fraction before proceeding with the division.
Let's divide 1 1/2 by 1/4:
-
Convert the mixed number to an improper fraction: 1 1/2 = (1 x 2 + 1) / 2 = 3/2
-
Rewrite as multiplication: 3/2 ÷ 1/4 = 3/2 x 4/1
-
Multiply numerators: 3 x 4 = 12
-
Multiply denominators: 2 x 1 = 2
-
Simplify: 12/2 = 6
Therefore, 1 1/2 divided by 1/4 is equal to 6.
Real-World Applications of Fraction Division
Fraction division isn't just a theoretical exercise; it has numerous practical applications in everyday life:
-
Cooking: Scaling recipes up or down often requires dividing fractions. For example, if a recipe calls for 1/2 cup of flour, and you want to make half the recipe, you need to divide 1/2 by 2.
-
Sewing and Crafting: Cutting fabric or other materials accurately involves fraction division.
-
Construction and Engineering: Precise measurements and calculations frequently involve dividing fractions to determine the required materials or dimensions.
-
Finance: Calculating portions of investments, shares, or budgets often necessitates fraction division.
Troubleshooting Common Mistakes
Several common pitfalls can arise when working with fraction division. Let's address some of these:
-
Forgetting to take the reciprocal: The most frequent error is forgetting to flip the second fraction (the divisor) before multiplying. Remember, dividing by a fraction is equivalent to multiplying by its reciprocal.
-
Incorrect multiplication: Carefully multiply the numerators and denominators. A simple calculation error can lead to an incorrect result.
-
Improper simplification: Always simplify the resulting fraction to its lowest terms. This helps to ensure the answer is in its most concise and accurate form.
Conclusion: Mastering Fraction Division
Mastering fraction division is a valuable skill with widespread applications. By understanding the underlying principles, practicing the steps, and visualizing the process, you can build confidence and proficiency in this crucial area of mathematics. Remember the key concept: dividing by a fraction is the same as multiplying by its reciprocal. With consistent practice, fraction division will become second nature. This comprehensive guide provides a solid foundation for tackling more complex fraction operations and real-world problems involving fractions. Continue practicing, and you will steadily enhance your mathematical skills. Remember to always double-check your work and utilize visual aids to help solidify your understanding. The more you practice, the easier it will become!
Latest Posts
Latest Posts
-
How Do You Graph Y 2 3x 1
May 12, 2025
-
Are Single Bonds Longer Than Double
May 12, 2025
-
How Is Photosynthesis And Cellular Respiration Connected
May 12, 2025
-
Is Alcohol An Acid Or Base
May 12, 2025
-
What Would Happen If The Earth Had No Atmosphere
May 12, 2025
Related Post
Thank you for visiting our website which covers about 5/8 Divided By 2 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.