5/6 Divided By 8 As A Fraction
listenit
May 10, 2025 · 5 min read
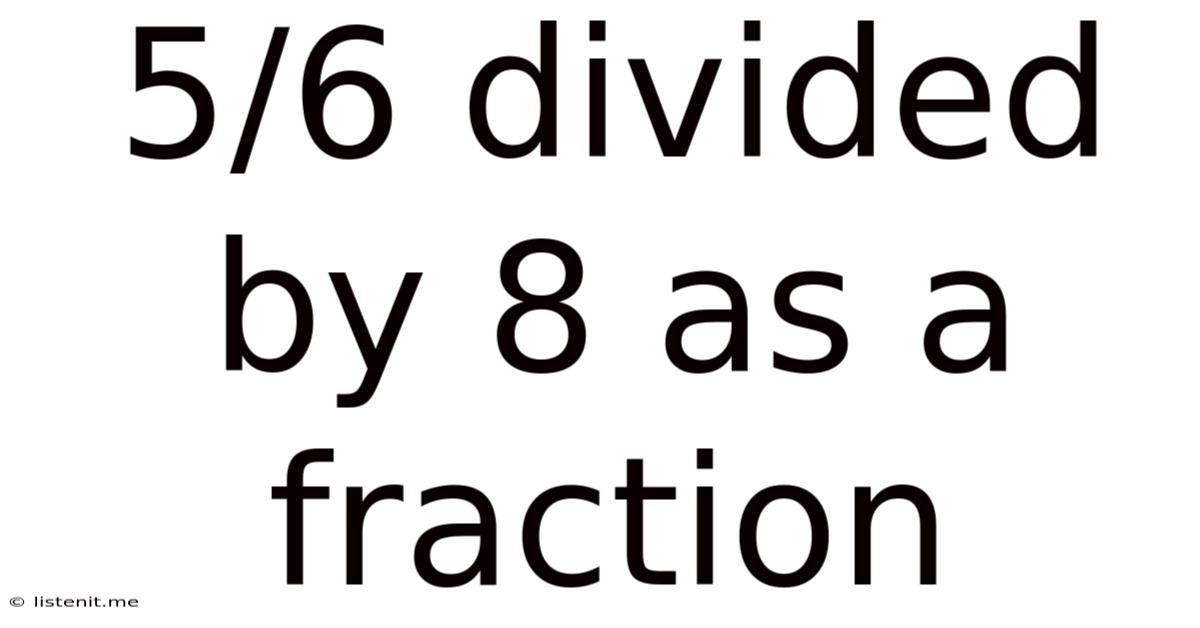
Table of Contents
5/6 Divided by 8: A Comprehensive Guide to Fraction Division
Dividing fractions can seem daunting at first, but with a clear understanding of the process, it becomes straightforward. This article delves into the detailed solution of 5/6 divided by 8, explaining the underlying principles and offering various approaches to solve similar problems. We'll explore different methods, emphasizing the importance of conceptual understanding alongside procedural fluency. This will empower you to tackle any fraction division problem with confidence.
Understanding Fraction Division
Before tackling our specific problem (5/6 ÷ 8), let's establish a solid foundation in fraction division. The core concept revolves around finding out "how many times" one fraction fits into another. This contrasts with multiplication, which finds the "product" of two fractions.
Key Concept: Dividing by a number is the same as multiplying by its reciprocal. The reciprocal of a number is simply 1 divided by that number. For example, the reciprocal of 8 is 1/8.
Method 1: Using the Reciprocal
This is the most common and efficient method for dividing fractions. The steps are as follows:
-
Rewrite the division problem as a multiplication problem: Change the division sign (÷) to a multiplication sign (×), and then invert (find the reciprocal of) the second fraction (or in this case, the whole number).
5/6 ÷ 8 becomes 5/6 × 1/8
-
Multiply the numerators: Multiply the numbers on the top (the numerators).
5 × 1 = 5
-
Multiply the denominators: Multiply the numbers on the bottom (the denominators).
6 × 8 = 48
-
Simplify the resulting fraction: If possible, reduce the fraction to its simplest form by finding the greatest common divisor (GCD) of the numerator and denominator. In this case, the GCD of 5 and 48 is 1. Therefore, the fraction is already in its simplest form.
Therefore, 5/6 ÷ 8 = 5/48
Method 2: Converting to a Common Denominator
This method offers a different perspective, providing a more intuitive understanding of fraction division.
-
Convert the whole number to a fraction: Express the whole number 8 as a fraction with a denominator of 1. This gives us 8/1.
-
Find a common denominator: Identify a common denominator for both fractions. In this case, the least common denominator (LCD) of 6 and 1 is 6.
-
Rewrite the fractions with the common denominator: Convert 5/6 to an equivalent fraction using the common denominator, which is already done. Convert 8/1 to an equivalent fraction by multiplying both the numerator and denominator by 6. That gives us 48/6.
-
Divide the numerators: Now, divide the numerator of the first fraction by the numerator of the second fraction: 5 ÷ 48 = 5/48
Therefore, 5/6 ÷ 8 = 5/48
Method 3: Visual Representation
While not as efficient for complex problems, visualizing the fraction division can enhance understanding, particularly for beginners.
Imagine you have a pizza cut into 6 equal slices. You have 5 of those slices (5/6 of a pizza). Now you want to divide this 5/6 of a pizza equally among 8 people. Each person will receive a much smaller portion than 1/6 of the original pizza.
This visual representation helps to understand why the result (5/48) is a smaller fraction than the original (5/6). Each person receives a tiny fraction (5/48) of the whole pizza.
Practical Applications and Real-World Examples
Understanding fraction division isn't just about solving textbook problems; it has numerous real-world applications. Consider these scenarios:
-
Recipe Scaling: If a recipe calls for 5/6 of a cup of flour and you want to make only 1/8 of the recipe, you would need to calculate (5/6) ÷ 8 = 5/48 cup of flour.
-
Sharing Resources: Imagine dividing 5/6 of a land equally among 8 people; each person receives 5/48 of the land.
-
Measurements: When working with precise measurements in fields like engineering or carpentry, fraction division becomes essential for accurate calculations.
Addressing Common Mistakes
Several common pitfalls can lead to incorrect answers when dividing fractions:
-
Forgetting to find the reciprocal: This is the most frequent error. Remember that you must invert the second fraction (or whole number expressed as a fraction) before multiplying.
-
Incorrect multiplication: Ensure you multiply numerators with numerators and denominators with denominators correctly.
-
Failure to simplify: Always simplify your final fraction to its lowest terms for a complete and accurate answer.
Advanced Concepts and Extensions
While we focused on dividing a fraction by a whole number, the same principles apply to dividing fractions by other fractions:
For example, let's solve (5/6) ÷ (2/3):
-
Rewrite as multiplication: (5/6) × (3/2)
-
Multiply numerators: 5 × 3 = 15
-
Multiply denominators: 6 × 2 = 12
-
Simplify: 15/12 simplifies to 5/4 (by dividing both numerator and denominator by 3)
Therefore, (5/6) ÷ (2/3) = 5/4
Conclusion: Mastering Fraction Division
Dividing fractions, though initially challenging, becomes manageable with consistent practice and a clear understanding of the underlying concepts. By mastering the reciprocal method or the common denominator method, you can confidently tackle any fraction division problem, from simple calculations to complex applications in various fields. Remember to always check your work and simplify your final answers for accurate and complete results. The ability to work confidently with fractions is a valuable mathematical skill with wide-ranging practical applications. Through consistent practice and a focus on understanding the underlying principles, you can become proficient in fraction division and apply this knowledge to real-world situations.
Latest Posts
Latest Posts
-
What Percent Of 22 Is 55
May 11, 2025
-
Are Ionic Compounds Made Of Metals And Nonmetals
May 11, 2025
-
How Much Is A 1000 Feet
May 11, 2025
-
Why Is Dissolving A Physical Change
May 11, 2025
-
Is Water Pure Substance Or Mixture
May 11, 2025
Related Post
Thank you for visiting our website which covers about 5/6 Divided By 8 As A Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.