5/6 As A Fraction In Simplest Form
listenit
May 24, 2025 · 5 min read
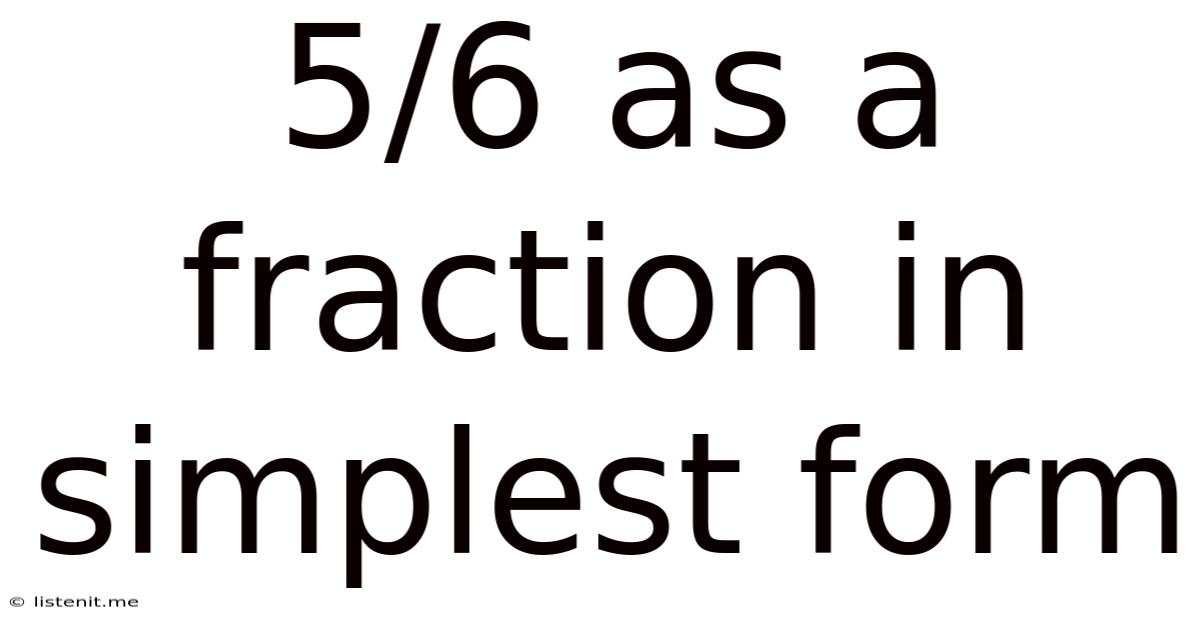
Table of Contents
5/6 as a Fraction in Simplest Form: A Comprehensive Guide
Understanding fractions is a fundamental skill in mathematics, forming the bedrock for more advanced concepts. While seemingly simple, mastering fractions requires a thorough grasp of their properties, including simplification. This article delves deep into the fraction 5/6, exploring its simplest form, and providing a comprehensive understanding of fraction simplification in general. We'll also touch upon related concepts and practical applications.
What is a Fraction?
A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates the total number of equal parts the whole is divided into, while the numerator indicates how many of those parts are being considered. For example, in the fraction 5/6, 6 represents the total number of equal parts, and 5 represents the number of parts we're interested in.
Understanding Simplest Form (Lowest Terms)
A fraction is in its simplest form, or lowest terms, when the numerator and the denominator have no common factors other than 1. In other words, the greatest common divisor (GCD) of the numerator and denominator is 1. Simplifying a fraction means reducing it to its simplest form. This makes the fraction easier to understand and work with.
Is 5/6 in Simplest Form?
The question posed is whether 5/6 is in its simplest form. To determine this, we need to find the greatest common divisor (GCD) of 5 and 6.
The factors of 5 are 1 and 5. The factors of 6 are 1, 2, 3, and 6.
The only common factor of 5 and 6 is 1. Therefore, 5/6 is already in its simplest form. It cannot be reduced further.
Methods for Simplifying Fractions
While 5/6 is already simplified, let's explore the general methods for simplifying fractions:
1. Finding the Greatest Common Divisor (GCD)
The most reliable method for simplifying fractions is to find the GCD of the numerator and denominator. The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder. There are several ways to find the GCD:
-
Listing Factors: This method involves listing all the factors of both the numerator and the denominator and identifying the largest common factor. This is straightforward for smaller numbers but can become cumbersome for larger numbers.
-
Prime Factorization: This method involves expressing both the numerator and the denominator as a product of their prime factors. The GCD is then the product of the common prime factors raised to the lowest power. For example, let's simplify 12/18:
12 = 2 x 2 x 3 = 2² x 3 18 = 2 x 3 x 3 = 2 x 3²
The common prime factors are 2 and 3. The lowest power of 2 is 2¹, and the lowest power of 3 is 3¹. Therefore, the GCD is 2 x 3 = 6. Dividing both the numerator and the denominator by 6 gives us 2/3, which is the simplified fraction.
-
Euclidean Algorithm: This is an efficient algorithm for finding the GCD of two numbers. It involves repeatedly applying the division algorithm until the remainder is 0. The last non-zero remainder is the GCD.
2. Dividing by Common Factors
A simpler approach, suitable for smaller numbers, is to identify common factors and divide both the numerator and the denominator by those factors. For instance, to simplify 12/18, we can see that both 12 and 18 are divisible by 2:
12/18 = (12 ÷ 2) / (18 ÷ 2) = 6/9
Now, we see that both 6 and 9 are divisible by 3:
6/9 = (6 ÷ 3) / (9 ÷ 3) = 2/3
This method is less systematic than finding the GCD directly but can be quicker for simple fractions.
Practical Applications of Fraction Simplification
Simplifying fractions is crucial in various applications:
-
Calculations: Simpler fractions make calculations easier and reduce the risk of errors. For instance, adding 1/2 and 1/4 is simpler than adding 2/4 and 1/4.
-
Comparisons: Simplifying fractions makes comparing their sizes easier. It's much easier to compare 1/2 and 2/3 than to compare 6/12 and 8/12.
-
Real-world problems: Fractions frequently appear in everyday situations, from cooking recipes to calculating distances. Simplifying them helps in interpreting results accurately. For example, if a recipe calls for 6/12 of a cup of sugar, simplifying this to 1/2 cup makes it more practical.
-
Algebra and higher mathematics: A solid understanding of fraction simplification is essential for more advanced mathematical concepts like algebra, calculus, and more.
Beyond 5/6: Exploring Other Fractions
Let's explore simplifying some other fractions to further solidify our understanding:
-
12/16: The GCD of 12 and 16 is 4. Therefore, 12/16 simplifies to 3/4.
-
24/36: The GCD of 24 and 36 is 12. Therefore, 24/36 simplifies to 2/3.
-
35/49: The GCD of 35 and 49 is 7. Therefore, 35/49 simplifies to 5/7.
-
15/25: The GCD of 15 and 25 is 5. Therefore, 15/25 simplifies to 3/5.
Improper Fractions and Mixed Numbers
It's important to note that fractions can be proper or improper. A proper fraction has a numerator smaller than the denominator (e.g., 5/6), while an improper fraction has a numerator greater than or equal to the denominator (e.g., 7/3). Improper fractions can be converted into mixed numbers, which consist of a whole number and a proper fraction (e.g., 2 1/3). Simplifying is still applied to the fractional part of a mixed number.
Conclusion
In conclusion, the fraction 5/6 is already in its simplest form because the greatest common divisor of 5 and 6 is 1. Understanding how to simplify fractions is a crucial skill in mathematics, essential for accurate calculations, comparisons, and problem-solving. Mastering various simplification methods, including finding the GCD using different techniques, helps in efficiently reducing fractions to their simplest forms, improving comprehension and making mathematical operations more manageable. From simple arithmetic to advanced calculus, this fundamental concept remains pivotal throughout your mathematical journey. The ability to effortlessly simplify fractions serves as a building block for more complex concepts and problem-solving skills, paving the way for a deeper and more complete understanding of mathematical principles.
Latest Posts
Latest Posts
-
6 1 8 As An Improper Fraction
May 24, 2025
-
What Is 3 5 Of 350 000
May 24, 2025
-
Greatest Common Factor Of 45 And 63
May 24, 2025
-
How Many Days Has It Been Since September 19
May 24, 2025
-
Find The Value Of In The Triangle Shown Below
May 24, 2025
Related Post
Thank you for visiting our website which covers about 5/6 As A Fraction In Simplest Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.