5 5/9 Divided By 2 2/3
listenit
May 23, 2025 · 5 min read
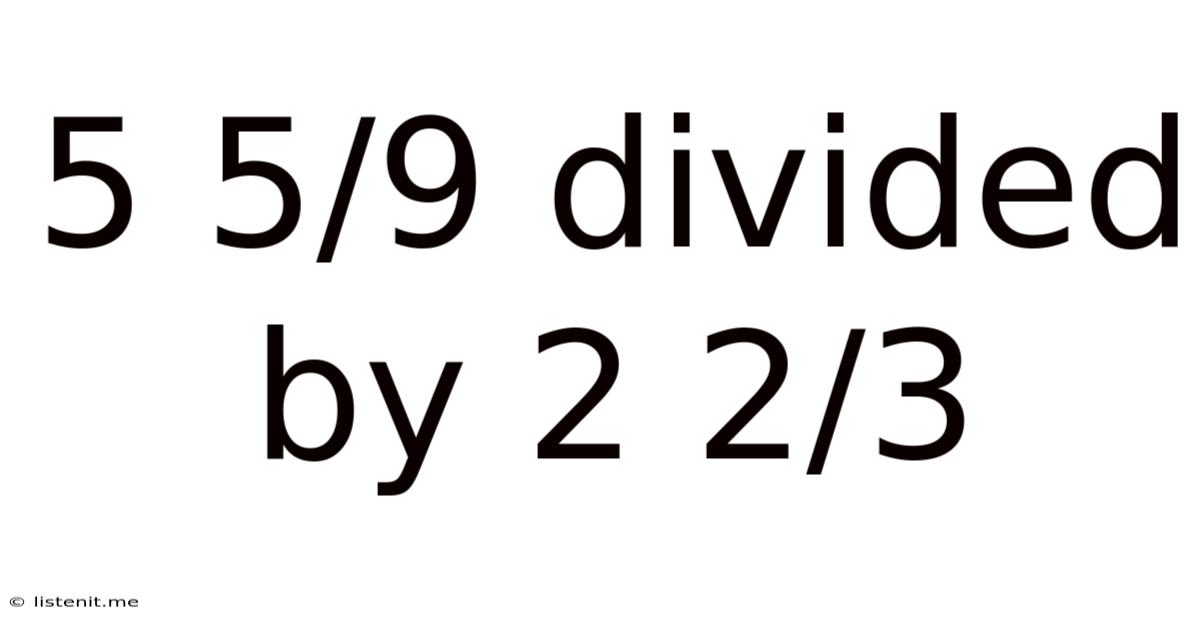
Table of Contents
5 5/9 Divided by 2 2/3: A Comprehensive Guide to Fraction Division
Dividing fractions, especially mixed numbers like 5 5/9 divided by 2 2/3, can seem daunting at first. However, with a systematic approach and a solid understanding of the underlying principles, this seemingly complex calculation becomes manageable and even straightforward. This comprehensive guide will not only walk you through the steps of solving 5 5/9 divided by 2 2/3 but also equip you with the knowledge to tackle similar problems with confidence. We’ll explore various methods, emphasizing conceptual understanding alongside practical application.
Understanding Fractions and Mixed Numbers
Before diving into the division problem, let's refresh our understanding of fractions and mixed numbers.
Fractions: A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The denominator indicates the total number of equal parts the whole is divided into, and the numerator indicates how many of those parts are being considered.
Mixed Numbers: A mixed number combines a whole number and a fraction. For example, 5 5/9 represents five whole units and five-ninths of another unit.
Converting Mixed Numbers to Improper Fractions
To divide fractions effectively, it's generally easier to work with improper fractions. An improper fraction is one where the numerator is greater than or equal to the denominator. Converting mixed numbers to improper fractions involves these steps:
- Multiply the whole number by the denominator: For 5 5/9, we multiply 5 by 9, which equals 45.
- Add the numerator: Add the result from step 1 to the numerator of the original fraction: 45 + 5 = 50.
- Keep the denominator: The denominator remains the same.
Therefore, 5 5/9 becomes 50/9. Similarly, 2 2/3 converts to 8/3.
Method 1: The Reciprocal Method (Invert and Multiply)
This is the most common and arguably the easiest method for dividing fractions. The process involves inverting (reciprocating) the second fraction and then multiplying the two fractions.
Steps:
- Convert mixed numbers to improper fractions: As shown above, 5 5/9 becomes 50/9 and 2 2/3 becomes 8/3.
- Invert the second fraction (the divisor): The reciprocal of 8/3 is 3/8.
- Multiply the first fraction by the reciprocal of the second fraction: This gives us (50/9) * (3/8).
- Simplify before multiplying (optional but recommended): Notice that we can simplify before multiplying. The number 50 is divisible by 10, and 8 is divisible by 2. Furthermore 9 is divisible by 3. This simplifies the calculation significantly. First cancel out the common factor of 3 between 9 and 3 reducing the fraction to (50/3) * (1/8). Then, the common factor of 2 between 50 and 8 can be cancelled. This yields (25/3) * (1/4).
- Multiply the numerators and the denominators: (25/3) * (1/4) = 25/12.
- Convert back to a mixed number (if required): To express 25/12 as a mixed number, divide 25 by 12. This gives us 2 with a remainder of 1. Therefore, 25/12 is equal to 2 1/12.
Therefore, 5 5/9 divided by 2 2/3 is 2 1/12.
Method 2: Using Long Division with Fractions
This method offers a more visual approach, especially helpful for those who prefer a step-by-step breakdown.
- Convert mixed numbers to improper fractions: Again, we have 50/9 and 8/3.
- Set up the long division: This will look like (50/9) ÷ (8/3).
- Rewrite as a multiplication problem using the reciprocal: This becomes (50/9) x (3/8).
- Multiply the numerators and denominators: 50 x 3 = 150 and 9 x 8 = 72. This gives us 150/72.
- Simplify the resulting fraction: Both 150 and 72 are divisible by 6, resulting in 25/12.
- Convert to a mixed number: As before, 25/12 simplifies to 2 1/12.
Method 3: Converting to Decimals (Less Accurate)
While this method is less precise due to potential rounding errors, it can be useful for estimations or when using a calculator.
- Convert fractions to decimals: 5 5/9 is approximately 5.555... and 2 2/3 is approximately 2.666...
- Divide the decimal numbers: 5.555... ÷ 2.666... ≈ 2.083
- Approximate the result: This is approximately 2 1/12. This method is prone to rounding errors, particularly if you are not using sufficient decimal places.
Practical Applications and Real-World Examples
Understanding fraction division isn't just about solving math problems; it has numerous real-world applications:
- Cooking and Baking: Dividing ingredients for recipes when scaling up or down. For instance, if a recipe calls for 2 2/3 cups of flour but you want to make half the recipe, you'd divide 2 2/3 by 2.
- Construction and Engineering: Calculating material quantities, dividing lengths, and determining proportions.
- Sewing and Crafting: Cutting fabric or other materials into specific sizes and proportions.
- Data Analysis: Working with data sets where fractions are involved in calculations.
Further Practice and Expanding Your Skills
Mastering fraction division requires consistent practice. Try solving similar problems with varying levels of complexity. Experiment with different methods to find the approach you find most comfortable and efficient. The key is to understand the underlying principles – converting mixed numbers, reciprocals, and simplifying fractions. With enough practice, you’ll be able to tackle any fraction division problem with confidence.
Troubleshooting Common Mistakes
- Forgetting to convert mixed numbers: Always convert mixed numbers to improper fractions before performing the division.
- Inverting the wrong fraction: Remember to invert only the second fraction (the divisor).
- Incorrect simplification: Pay close attention to simplifying fractions to reduce computational complexity and potential errors.
- Rounding Errors (when using decimals): Be aware that rounding during decimal conversions can lead to inaccuracies in the final result.
Conclusion: Mastering Fraction Division
Dividing fractions, especially mixed numbers, is a fundamental skill in mathematics with broad applications. By understanding the different methods, practicing regularly, and avoiding common errors, you can develop a confident and efficient approach to solving these problems. Remember to always focus on a clear understanding of the underlying concepts. With consistent effort, the once-challenging task of dividing fractions will become second nature. This will open up a wider range of mathematical and real-world problems you can confidently solve. Remember to always check your work and practice regularly to build your proficiency.
Latest Posts
Latest Posts
-
What Is The Greatest Common Factor Of 16 And 72
May 23, 2025
-
30 Days From July 16 2024
May 23, 2025
-
What Time Will It Be In 100 Hours
May 23, 2025
-
10 Out Of 18 As A Percentage
May 23, 2025
-
What Is 70 Percent Off 30 Dollars
May 23, 2025
Related Post
Thank you for visiting our website which covers about 5 5/9 Divided By 2 2/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.