5/14 Divided By 7/8 In Simplest Form
listenit
May 24, 2025 · 4 min read
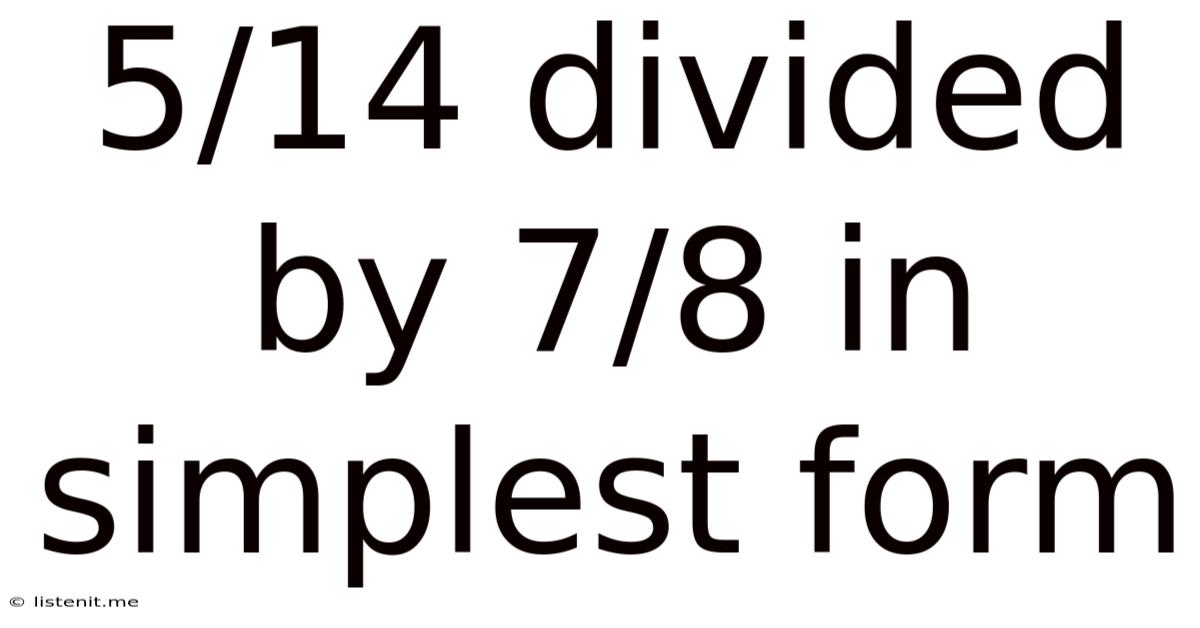
Table of Contents
5/14 Divided by 7/8 in Simplest Form: A Comprehensive Guide
Dividing fractions can seem daunting at first, but with a clear understanding of the process and a bit of practice, it becomes straightforward. This article will comprehensively guide you through solving 5/14 divided by 7/8, explaining the steps involved, providing alternative methods, and exploring related concepts to solidify your understanding of fraction division. We'll also delve into the broader context of fraction operations and their real-world applications.
Understanding Fraction Division
Before tackling the specific problem of 5/14 ÷ 7/8, let's establish a solid foundation in fraction division. The core principle is to invert the second fraction (the divisor) and multiply. This is equivalent to multiplying by the reciprocal.
The Reciprocal: The reciprocal of a fraction is obtained by swapping the numerator and the denominator. For example, the reciprocal of 7/8 is 8/7.
Therefore, the general rule for dividing fractions is:
a/b ÷ c/d = a/b * d/c
Solving 5/14 ÷ 7/8 Step-by-Step
Now, let's apply this rule to our problem: 5/14 ÷ 7/8
-
Invert the second fraction: The reciprocal of 7/8 is 8/7.
-
Change the division to multiplication: Our problem now becomes: 5/14 * 8/7
-
Multiply the numerators: 5 * 8 = 40
-
Multiply the denominators: 14 * 7 = 98
-
Result: The result of the multiplication is 40/98.
-
Simplify the fraction: Both 40 and 98 are even numbers, meaning they are divisible by 2. Let's simplify by dividing both the numerator and the denominator by their greatest common divisor (GCD).
- 40 ÷ 2 = 20
- 98 ÷ 2 = 49
Therefore, 40/98 simplifies to 20/49. Since 20 and 49 share no common factors other than 1, this is the simplest form.
Alternative Methods and Visual Representations
While the method above is the most common and efficient, let's explore alternative approaches to enhance your understanding:
Method 1: Using Common Denominators
Although less efficient for this specific problem, understanding this method is beneficial for grasping the underlying principles of fraction division. This method involves finding a common denominator for both fractions and then dividing the numerators.
-
Find a common denominator: The least common multiple (LCM) of 14 and 8 is 56.
-
Convert fractions to equivalent fractions with the common denominator:
- 5/14 = 20/56 (multiplied numerator and denominator by 4)
- 7/8 = 49/56 (multiplied numerator and denominator by 7)
-
Divide the numerators: 20 ÷ 49 = 20/49
This method leads to the same simplified answer: 20/49.
Method 2: Visual Representation with Area Models
Visual representations can be incredibly helpful, especially for beginners. Imagine a rectangle representing 1 whole unit. You can divide this rectangle to represent 5/14 and then further divide it to illustrate the division by 7/8. While this method becomes complex for larger numbers, it offers a strong intuitive understanding of fraction division.
Expanding on Fraction Operations
Understanding fraction division is crucial because it forms the basis for numerous mathematical concepts and real-world applications. Let's briefly touch upon other fraction operations and their significance:
Fraction Addition and Subtraction
Adding and subtracting fractions require a common denominator. Once the denominators are the same, you simply add or subtract the numerators and keep the denominator unchanged. For example:
1/2 + 1/4 = (2/4) + (1/4) = 3/4
Fraction Multiplication
Multiplying fractions is straightforward: multiply the numerators together and multiply the denominators together. For example:
1/2 * 1/4 = 1/8
Real-World Applications of Fraction Division
Fraction division isn't just an abstract mathematical concept; it's used extensively in various real-world scenarios:
-
Cooking and Baking: Scaling recipes up or down requires dividing fractions. If a recipe calls for 1/2 cup of flour and you want to make half the recipe, you need to divide 1/2 by 2.
-
Sewing and Tailoring: Cutting fabric accurately often involves dividing fractions to determine the required lengths.
-
Construction and Engineering: Calculating material quantities and dimensions frequently involves fraction division.
-
Data Analysis: Working with proportions and percentages often involves fraction division.
Further Practice and Resources
Mastering fraction division takes practice. Work through various problems, starting with simpler ones and gradually increasing the complexity. Online resources and educational websites offer numerous practice problems and interactive exercises to enhance your understanding. Remember to always simplify your answers to their lowest terms.
Conclusion: Mastering Fraction Division
We've comprehensively explored the process of dividing 5/14 by 7/8, arriving at the simplest form of 20/49. We've also examined alternative methods and discussed the broader context of fraction operations and their relevance in daily life. Remember, consistent practice and a solid grasp of the fundamental principles are key to mastering fraction division and confidently tackling more complex mathematical problems. Through understanding the underlying concepts and applying the techniques discussed, you'll build a strong foundation in fractions and enhance your problem-solving abilities in various fields.
Latest Posts
Latest Posts
-
What Is The Greatest Common Factor Of 6 And 20
May 24, 2025
-
How Many Btu To Heat 900 Sq Ft
May 24, 2025
-
Where Is The Calculator On The Ww App
May 24, 2025
-
What Is 30 Percent Of 125
May 24, 2025
-
Greatest Common Factor Of 24 And 84
May 24, 2025
Related Post
Thank you for visiting our website which covers about 5/14 Divided By 7/8 In Simplest Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.