45 Is 12 Of What Number
listenit
May 11, 2025 · 4 min read
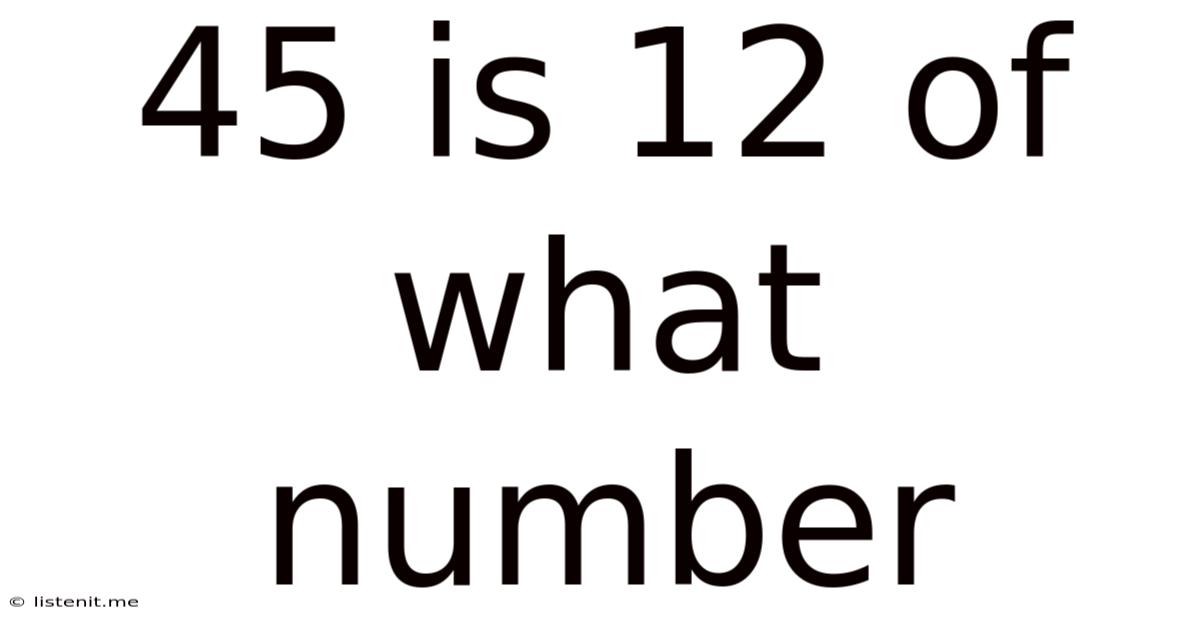
Table of Contents
45 is 12% of What Number? A Comprehensive Guide to Percentage Calculations
Finding the whole when you know a part and its percentage is a fundamental skill in mathematics with broad applications in everyday life, from calculating discounts and sales tax to understanding financial reports and interpreting statistical data. This article will delve into the solution for the problem "45 is 12% of what number?", exploring multiple methods and providing a thorough understanding of the underlying principles of percentage calculations. We'll also discuss the practical applications and potential pitfalls to avoid.
Understanding the Problem: Deconstructing Percentages
Before jumping into the calculations, let's break down the problem statement: "45 is 12% of what number?" This sentence translates into a mathematical equation where we need to find the unknown value (let's call it 'x'). The problem can be represented as:
45 = 0.12 * x
This equation highlights the core relationship between the percentage, the part, and the whole. We have the part (45), the percentage (12%), and we need to solve for the whole (x).
Method 1: Using the Percentage Formula
The most straightforward approach is to use the basic percentage formula, which is:
(Part / Whole) * 100% = Percentage
In our case, we know the part (45) and the percentage (12%). We need to solve for the whole (x). Rearranging the formula to solve for x, we get:
Whole (x) = (Part / Percentage) * 100
Substituting the known values:
x = (45 / 12) * 100
x = 3.75 * 100
x = 375
Therefore, 45 is 12% of 375.
Method 2: Solving the Equation Directly
As mentioned earlier, the problem can be represented by the equation:
45 = 0.12 * x
To solve for x, we can use algebraic manipulation:
-
Divide both sides by 0.12: This isolates x on one side of the equation.
45 / 0.12 = x -
Perform the division: This gives us the value of x.
375 = x
Therefore, once again, we find that x = 375.
Method 3: Using Proportions
The concept of percentages can be easily understood using proportions. We can set up a proportion to solve for the unknown value:
12/100 = 45/x
This proportion states that the ratio of 12 to 100 (representing 12%) is equal to the ratio of 45 to the unknown number (x). To solve for x, we can cross-multiply:
12 * x = 45 * 100
12x = 4500
x = 4500 / 12
x = 375
This method provides another way to arrive at the same solution, reinforcing the underlying relationship between the parts and the whole.
Practical Applications: Real-World Examples
The ability to calculate percentages and solve for the whole is crucial in various real-life situations. Here are a few examples:
-
Sales and Discounts: If a store offers a 20% discount on an item and the discount amount is $30, you can use this method to determine the original price of the item.
-
Taxes: Calculating sales tax or income tax often involves working with percentages. Understanding how to find the original amount before tax is applied is essential for managing personal finances.
-
Financial Investments: Calculating returns on investments, understanding interest rates, and analyzing investment growth all involve working with percentages and proportions.
-
Statistical Analysis: Percentages are frequently used in statistical data to represent proportions and trends. Understanding how to interpret percentage data is vital in various fields, including business, healthcare, and research.
-
Surveys and Polls: Results from surveys and polls are often expressed as percentages. Understanding how to calculate the total number of respondents based on a percentage of responses is essential for accurate interpretation.
Common Mistakes to Avoid
While percentage calculations are relatively straightforward, several common mistakes can lead to inaccurate results. Here are a few pitfalls to watch out for:
-
Incorrect Conversion of Percentages to Decimals: Remember to convert percentages to decimals before performing calculations. For example, 12% should be converted to 0.12.
-
Incorrect Formula Application: Ensure you're using the correct formula and substituting the correct values into the equation.
-
Calculation Errors: Double-check your calculations to avoid arithmetic mistakes, especially when working with decimals.
-
Misinterpretation of the Problem: Carefully read the problem statement to ensure you understand what is being asked. Identify the known values (part and percentage) and the unknown value (the whole).
Expanding Your Understanding: Beyond the Basics
This article has focused on a specific percentage problem. However, the principles discussed here can be applied to a wide range of percentage calculations. You can use similar methods to:
- Calculate the percentage of a number: Find what percentage one number represents of another.
- Calculate percentage increase or decrease: Determine the percentage change between two values.
- Calculate percentage points: Understand the difference between percentage change and percentage points.
Conclusion: Mastering Percentage Calculations
Understanding how to solve problems like "45 is 12% of what number?" is a valuable skill that extends far beyond the classroom. By mastering the various methods presented in this article, you'll gain confidence in handling percentage calculations and confidently tackle real-world problems involving percentages, proportions, and ratios. Remember to practice regularly, paying close attention to detail and avoiding common errors. With consistent effort, you'll become proficient in applying these fundamental mathematical concepts to various scenarios. The ability to accurately and efficiently perform these calculations is a significant asset in numerous aspects of life, from personal finance to professional success.
Latest Posts
Latest Posts
-
What Is The Relationship Between Temperature And Pressure
May 12, 2025
-
How To Find Y Intercept With Slope And A Point
May 12, 2025
-
What Would Happen If The Earth Had No Tilt
May 12, 2025
-
How To Find The Area Under A Normal Distribution Curve
May 12, 2025
-
What Is 4 36 In Simplest Form
May 12, 2025
Related Post
Thank you for visiting our website which covers about 45 Is 12 Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.