40 Percent Of What Number Is 20
listenit
May 13, 2025 · 5 min read
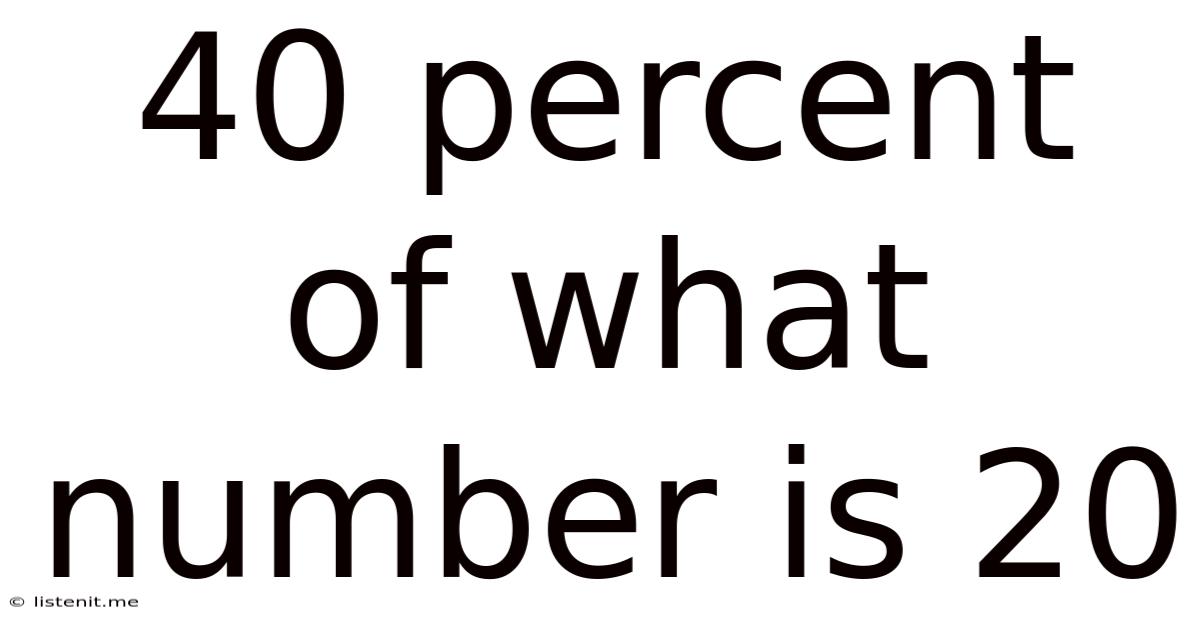
Table of Contents
40 Percent of What Number is 20? A Comprehensive Guide to Percentage Calculations
Solving the equation "40 percent of what number is 20" might seem simple at first glance. However, understanding the underlying principles of percentage calculations is crucial for tackling more complex problems in various fields, from finance and statistics to everyday life scenarios. This comprehensive guide will not only solve this specific problem but also equip you with the knowledge and tools to tackle similar percentage problems with confidence.
Understanding Percentages
Before diving into the solution, let's establish a solid understanding of percentages. A percentage is a fraction or ratio expressed as a number out of 100. For example, 40% means 40 out of 100, which can be written as the fraction 40/100 or the decimal 0.40. This fundamental understanding forms the basis for all percentage calculations.
Key Concepts in Percentage Calculations
- Percentage: The portion of a whole represented as a number out of 100.
- Whole (or Base): The total amount or quantity that the percentage refers to. In our problem, this is the unknown number we're trying to find.
- Part: The portion of the whole represented by the percentage. In our problem, the part is 20.
Solving "40 Percent of What Number is 20?"
We can approach this problem using several methods. Let's explore the most common and effective ones:
Method 1: Using the Equation
The most straightforward method involves setting up an equation:
40% * x = 20
Where 'x' represents the unknown number we're trying to find. To solve for 'x', we follow these steps:
-
Convert the percentage to a decimal: 40% = 0.40
-
Rewrite the equation: 0.40 * x = 20
-
Isolate 'x': Divide both sides of the equation by 0.40:
x = 20 / 0.40
-
Calculate 'x': x = 50
Therefore, 40% of 50 is 20.
Method 2: Using Proportions
Proportions offer another effective way to solve percentage problems. We can set up a proportion as follows:
40/100 = 20/x
This proportion states that the ratio of 40 to 100 is equal to the ratio of 20 to the unknown number (x). To solve for x, we cross-multiply:
40 * x = 20 * 100
40x = 2000
x = 2000 / 40
x = 50
Again, we find that x = 50.
Method 3: Working Backwards from the Percentage
This method involves thinking about the problem in reverse. If 40% of a number is 20, then 1% of that number would be 20/40 = 0.5. To find the whole number (100%), we simply multiply 0.5 by 100:
0.5 * 100 = 50
This method provides a quick and intuitive way to solve the problem, particularly for simpler percentage calculations.
Expanding on Percentage Calculations: Real-World Applications
Understanding percentage calculations is essential in numerous real-world situations. Let's explore some examples:
Finance
- Calculating discounts: If a store offers a 25% discount on an item priced at $80, the discount amount is 25% of $80, which is $20. The final price would be $60.
- Determining interest earned: If you invest $1000 at an annual interest rate of 5%, you'll earn 5% of $1000, or $50, in interest after one year.
- Analyzing financial statements: Percentage calculations are crucial for interpreting financial reports, comparing performance over time, and identifying trends. For example, calculating profit margins, return on investment (ROI), and debt-to-equity ratios all rely heavily on percentage calculations.
Statistics
- Analyzing survey data: Percentages are frequently used to represent survey results. For example, if 60% of respondents answered "yes" to a particular question, this indicates that 60 out of every 100 respondents gave a "yes" response.
- Calculating probabilities: Percentages are often used to express probabilities. For instance, a 70% chance of rain means there's a 70 out of 100 probability of rain.
- Interpreting statistical data: Percentage changes, percentage points, and various statistical measures are expressed using percentages, enabling easy comparison and interpretation of data.
Everyday Life
- Calculating tips: When dining out, calculating a tip (e.g., 15% or 20%) on the bill is a common application of percentages.
- Understanding sales tax: Sales tax is usually expressed as a percentage of the purchase price.
- Determining nutritional values: Nutritional information on food labels often presents values as percentages of recommended daily intakes.
Advanced Percentage Calculations: Tackling More Complex Problems
While the initial problem was relatively straightforward, percentage calculations can become more complex. Let's consider some advanced scenarios:
Calculating Percentage Increase or Decrease
These calculations involve determining the percentage change between two values. The formula is:
((New Value - Old Value) / Old Value) * 100%
For example, if a stock price increases from $50 to $60, the percentage increase is:
(($60 - $50) / $50) * 100% = 20%
Calculating Percentage Points
Percentage points represent the absolute difference between two percentages. For example, if the unemployment rate increases from 5% to 8%, the increase is 3 percentage points, not 3%. This distinction is crucial for accurate interpretation of data.
Solving for the Percentage
Sometimes, you might know the whole and the part, but need to find the percentage. For example, if 15 out of 50 students passed an exam, the percentage of students who passed is:
(15/50) * 100% = 30%
Mastering Percentage Calculations: Tips and Tricks
- Practice Regularly: The more you practice, the more comfortable you'll become with various percentage calculation methods.
- Use a Calculator: For complex calculations, a calculator can significantly improve accuracy and efficiency.
- Understand the Context: Always carefully analyze the problem statement to understand what you're being asked to calculate.
- Check Your Work: It's crucial to double-check your calculations to ensure accuracy, especially in situations where precision is paramount.
Conclusion
Solving "40 percent of what number is 20?" is a stepping stone to mastering percentage calculations. This guide has provided multiple methods for solving this specific problem and expanded on the broader applications of percentage calculations across various fields. By understanding the fundamental concepts and practicing regularly, you can confidently tackle more complex percentage problems and effectively use this crucial skill in your daily life, academic pursuits, and professional endeavors. Remember, the key is to practice consistently and apply your knowledge to diverse real-world scenarios. This will help solidify your understanding and build your confidence in tackling any percentage problem you encounter.
Latest Posts
Latest Posts
-
What Type Of Bond Holds Nitrogen Bases Together
May 13, 2025
-
Why Is Burning A Chemical Change
May 13, 2025
-
Parentheses Are Used To Introduce A Quotation
May 13, 2025
-
Which Orbital Has The Highest Energy
May 13, 2025
-
What Are The Two Landlocked Countries Of South America
May 13, 2025
Related Post
Thank you for visiting our website which covers about 40 Percent Of What Number Is 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.