40 Out Of 75 As A Percentage
listenit
May 09, 2025 · 5 min read
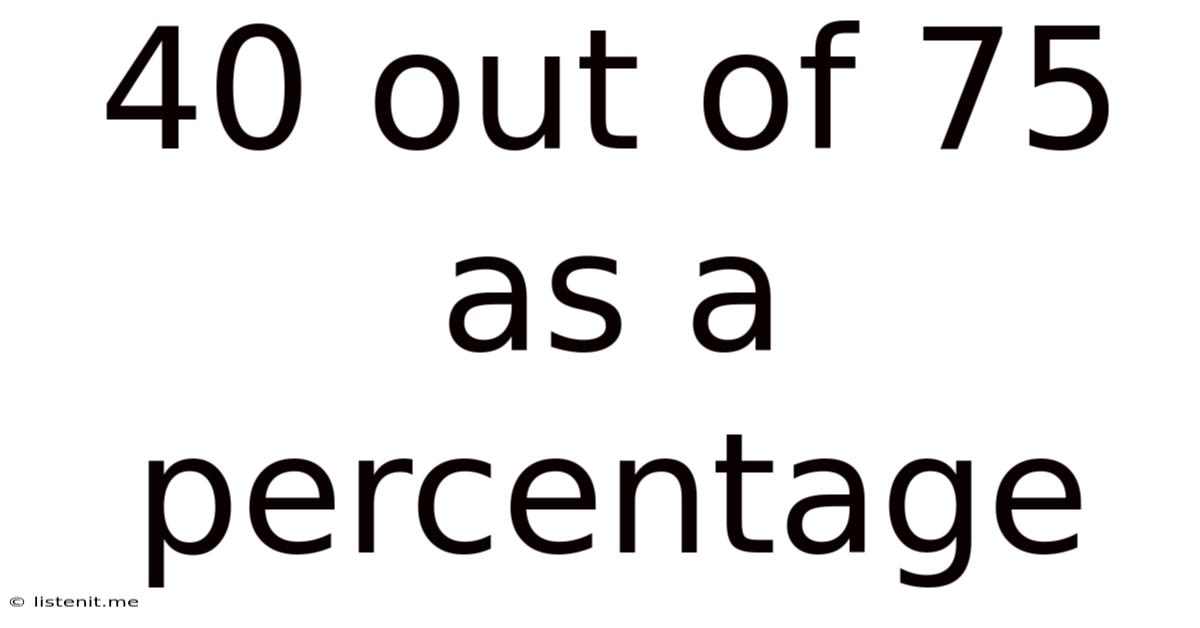
Table of Contents
40 out of 75 as a Percentage: A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill applicable across various fields, from academic assignments and financial planning to everyday decision-making. Understanding how to express a fraction as a percentage is crucial for interpreting data, making comparisons, and understanding proportions. This article will comprehensively guide you through calculating "40 out of 75 as a percentage," explaining the process step-by-step and expanding on the broader concept of percentage calculations.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "per hundred." Therefore, 50% means 50 out of 100, or 50/100, which simplifies to 1/2 or 0.5. Percentages are often used to represent proportions, rates, or changes in values. They provide a standardized way to compare different quantities.
Calculating 40 out of 75 as a Percentage
To determine what percentage 40 represents of 75, we'll follow a straightforward method:
-
Express as a Fraction: First, we express the given numbers as a fraction: 40/75. This means 40 out of a total of 75.
-
Convert to Decimal: Next, divide the numerator (40) by the denominator (75): 40 ÷ 75 = 0.53333...
-
Convert Decimal to Percentage: Multiply the decimal by 100 to convert it to a percentage: 0.53333... × 100 = 53.333...%
-
Rounding: Finally, we round the percentage to an appropriate number of decimal places. For most practical purposes, rounding to two decimal places is sufficient: 53.33%.
Therefore, 40 out of 75 is 53.33%.
Different Methods for Percentage Calculation
While the above method is the most common, there are alternative approaches to calculating percentages. Let's explore a few:
Method 2: Using Proportions
We can set up a proportion to solve this problem. Let 'x' represent the percentage we're trying to find:
40/75 = x/100
To solve for x, cross-multiply:
75x = 4000
x = 4000/75
x ≈ 53.33
Therefore, x ≈ 53.33%, confirming our previous result.
Method 3: Using a Calculator
Most calculators have a percentage function that simplifies the calculation. Simply enter 40 ÷ 75 and then multiply by 100 to get the percentage directly.
Practical Applications of Percentage Calculations
Understanding percentage calculations has broad applications across various aspects of life. Here are some examples:
1. Academic Performance:
Calculating grades, assessing test scores, and determining overall academic performance often involves percentage calculations. For instance, if a student scores 40 out of 75 on a test, understanding that it's equivalent to 53.33% helps gauge their performance relative to the total marks.
2. Financial Management:
Percentage calculations are essential in financial planning, investment analysis, and budgeting. Calculating interest rates, discounts, profit margins, and tax rates all involve percentages. For example, determining the percentage increase or decrease in investment value or calculating loan interest requires a thorough understanding of percentage calculations.
3. Sales and Marketing:
In sales and marketing, percentages are used to track sales performance, analyze market share, and calculate discounts and profit margins. For instance, calculating the percentage increase in sales compared to a previous period, or evaluating the success of a marketing campaign using percentage conversion rates, are critical aspects of business analysis.
4. Data Analysis and Statistics:
Percentages are commonly used in data analysis and statistics to represent proportions, probabilities, and relative frequencies. Understanding how to convert raw data into percentages allows for easier interpretation and comparison. For example, representing survey results or analyzing population statistics often involves calculating percentages.
5. Everyday Life:
Percentages are used in many everyday situations, such as calculating tips in restaurants, determining discounts on sale items, or understanding the nutritional information on food labels. These calculations help us make informed decisions in our daily lives.
Common Percentage Calculation Mistakes
While seemingly simple, percentage calculations can sometimes lead to errors. Here are some common mistakes to avoid:
-
Incorrect Order of Operations: Ensure you perform the division before multiplying by 100. Incorrect order can lead to inaccurate results.
-
Rounding Errors: Be mindful of rounding errors, especially when dealing with multiple percentage calculations. Rounding too early in the process can propagate errors, leading to significantly inaccurate results.
-
Confusing Percentage Change with Absolute Change: Percentage change represents the relative change, whereas absolute change is the difference between two values. Understanding the distinction between these two concepts is crucial for accurate interpretations.
-
Incorrect Interpretation of Percentage Points: A percentage point is the difference between two percentages, not the percentage difference. For instance, an increase from 50% to 55% is a 5 percentage point increase, but a 10% increase relative to the original 50%.
Advanced Percentage Calculations
Beyond the basic calculations, understanding more complex percentage concepts can broaden your analytical capabilities. Some advanced concepts include:
-
Compound Interest: This involves calculating interest on both the principal amount and accumulated interest.
-
Percentage Increase/Decrease: Calculating the percentage change between two values, considering both increases and decreases.
-
Percentage Points: As mentioned before, understanding the difference between percentage points and percentage changes.
-
Weighted Averages: Calculating averages where different data points have different weights or importance.
Mastering percentage calculations, from the simplest to the most advanced, opens doors to more sophisticated analysis and decision-making across various disciplines.
Conclusion
Calculating 40 out of 75 as a percentage – resulting in 53.33% – is a fundamental skill with wide-ranging applications. Understanding the methods involved, avoiding common errors, and exploring advanced concepts allows for confident and accurate interpretation of data and informed decision-making in numerous contexts. By grasping the principles outlined in this guide, you can confidently tackle percentage calculations in your academic, professional, and personal life. Remember to practice regularly to solidify your understanding and improve your speed and accuracy.
Latest Posts
Latest Posts
-
What Are Common Factors Of 18 And 30
May 09, 2025
-
What Adds To 2 And Multiplies To 3
May 09, 2025
-
What Structures Are Formed When Water Molecules Surrounds Individual Ions
May 09, 2025
-
Atoms Of The Same Element Are Exactly Alike
May 09, 2025
-
Which Type Of Wave Is A Sound Wave
May 09, 2025
Related Post
Thank you for visiting our website which covers about 40 Out Of 75 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.