40 Is 50 Of What Number
listenit
May 12, 2025 · 5 min read
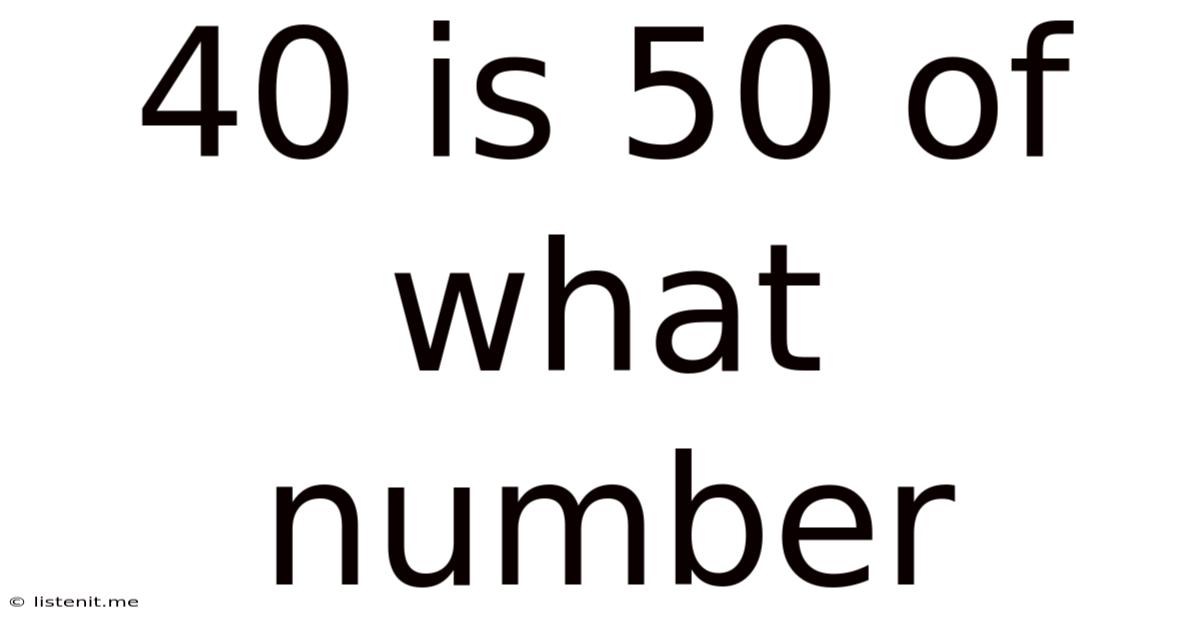
Table of Contents
40 is 50% of What Number? A Deep Dive into Percentage Calculations
This seemingly simple question, "40 is 50% of what number?", opens the door to a fascinating exploration of percentage calculations, their applications in everyday life, and the underlying mathematical principles. While the answer might seem immediately obvious to some, understanding the how and why behind the solution is crucial for mastering various percentage-related problems. This article will not only provide the answer but also delve into the methods of solving such problems, explain the concepts involved, and explore real-world applications.
Understanding Percentages: The Basics
Before we tackle the problem, let's solidify our understanding of percentages. A percentage is a way of expressing a number as a fraction of 100. The symbol "%" represents "per cent" or "out of 100". For example, 50% means 50 out of 100, which can be written as the fraction 50/100 or the decimal 0.5.
Understanding this fundamental concept is key to solving percentage problems. Many problems involve finding a percentage of a number, finding what percentage one number is of another, or finding the original number given a percentage and its resulting value. Our problem falls into the latter category.
Method 1: Using the Percentage Formula
The most straightforward approach to solving "40 is 50% of what number?" is using the basic percentage formula:
Part = Percentage × Whole
In our problem:
- Part: This is the value we already know – 40.
- Percentage: This is also known – 50%, which we convert to a decimal (0.5).
- Whole: This is the unknown value we need to find. Let's represent it with 'x'.
Substituting these values into the formula, we get:
40 = 0.5 × x
To solve for x, we need to isolate it. We can do this by dividing both sides of the equation by 0.5:
x = 40 / 0.5
x = 80
Therefore, 40 is 50% of 80.
Method 2: Using Proportions
Another effective method involves setting up a proportion. A proportion is an equation stating that two ratios are equal. We can represent our problem as:
40/x = 50/100
This proportion states that 40 is to x as 50 is to 100. To solve for x, we can cross-multiply:
40 × 100 = 50 × x
4000 = 50x
Now, divide both sides by 50:
x = 4000 / 50
x = 80
Again, we arrive at the solution: 40 is 50% of 80.
Method 3: Thinking in Reverse
A more intuitive, albeit less formal, approach involves thinking about the problem in reverse. If 40 represents 50%, we know that 50% is half of 100%. Therefore, to find the whole number, we simply double 40:
40 × 2 = 80
This method provides a quick and easy solution, highlighting the direct relationship between percentages and their corresponding whole numbers. However, it's important to note that this method is most effective when dealing with easily recognizable percentages like 50%, 25%, or 10%.
Real-World Applications of Percentage Calculations
Understanding percentage calculations isn't just about solving mathematical problems; it's a crucial skill applicable in numerous real-world scenarios. Here are some examples:
-
Sales and Discounts: Calculating discounts on sale items is a common application. If a store offers a 20% discount on an item originally priced at $100, you would calculate the discount as 0.20 × $100 = $20, and the final price would be $100 - $20 = $80.
-
Taxes and Interest: Calculating taxes or interest on loans or investments requires understanding percentages. For instance, if the sales tax is 6%, you'd calculate the tax on a $50 purchase as 0.06 × $50 = $3.
-
Tips and Gratuities: Calculating tips in restaurants often involves using percentages. A 15% tip on a $60 meal would be 0.15 × $60 = $9.
-
Financial Analysis: Percentage changes are used extensively in financial analysis to track growth or decline in various metrics, such as stock prices, revenue, or profits.
-
Statistical Analysis: Percentages are fundamental in statistical analysis to express proportions, probabilities, and data distributions.
-
Scientific Research: Many scientific calculations and experiments involve using percentages to represent data and results.
Beyond the Basics: More Complex Percentage Problems
While the problem "40 is 50% of what number?" is relatively straightforward, the principles involved can be extended to more complex scenarios. These might involve multiple percentages, unknown percentages, or multiple unknowns requiring simultaneous equations.
For example, consider this: "If a price increases by 10% and then decreases by 15%, what is the net percentage change?" Problems like these require a more nuanced understanding of percentage calculations and often involve a step-by-step approach to break down the problem into manageable parts.
Mastering Percentage Calculations: Tips and Strategies
Mastering percentage calculations requires consistent practice and a strong understanding of the underlying principles. Here are some helpful tips and strategies:
-
Convert Percentages to Decimals: Always convert percentages to their decimal equivalents before performing calculations. This makes the calculations more straightforward.
-
Use the Formula Consistently: Familiarize yourself with the basic percentage formula (Part = Percentage × Whole) and apply it systematically.
-
Check Your Work: Always double-check your calculations to ensure accuracy. Use alternative methods to verify your answers if possible.
-
Practice Regularly: The key to mastering any mathematical concept is consistent practice. Work through a variety of problems to improve your speed and accuracy.
-
Understand the Context: Pay close attention to the wording of percentage problems to understand what is being asked. Clearly identify the known and unknown variables.
Conclusion: The Power of Percentages
The seemingly simple question, "40 is 50% of what number?", provides a valuable entry point into the world of percentage calculations. While the answer is 80, the real value lies in understanding the methods used to arrive at that answer and the broad applications of these calculations in various aspects of life. By mastering percentage calculations, you equip yourself with a powerful tool for navigating numerous real-world situations, from managing personal finances to understanding complex data in various fields. The journey from a basic percentage problem to understanding its implications demonstrates the power of mathematical literacy and problem-solving skills.
Latest Posts
Latest Posts
-
What Would Happen If Photosynthesis Stopped Happening On Earth
May 12, 2025
-
How Many Protons Does Zirconium Have
May 12, 2025
-
Length Of A Polar Curve Formula
May 12, 2025
-
What Does It Mean For A Function To Be Bounded
May 12, 2025
-
Which Electromagnetic Waves Have The Shortest Wavelength
May 12, 2025
Related Post
Thank you for visiting our website which covers about 40 Is 50 Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.