4 Out Of 17 As A Percentage
listenit
May 26, 2025 · 5 min read
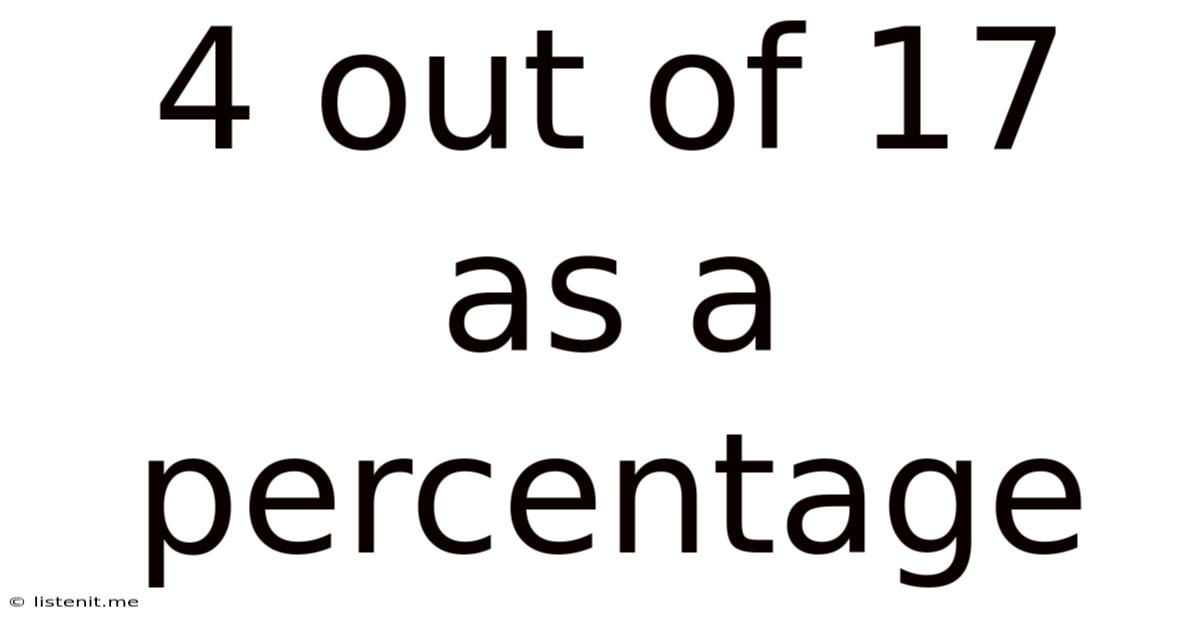
Table of Contents
4 out of 17 as a Percentage: A Comprehensive Guide
Calculating percentages is a fundamental skill applicable across various fields, from everyday budgeting to complex scientific analyses. Understanding how to convert fractions into percentages is crucial for interpreting data, making informed decisions, and communicating numerical information effectively. This comprehensive guide delves into calculating "4 out of 17 as a percentage," explaining the process step-by-step, providing various methods, and exploring related percentage calculations. We will also examine real-world applications to solidify your understanding.
Understanding Percentages
Before we dive into the specific calculation of 4 out of 17, let's establish a solid understanding of percentages. A percentage is a way of expressing a number as a fraction of 100. The word "percent" itself comes from the Latin "per centum," meaning "out of a hundred." Therefore, any percentage can be represented as a fraction with a denominator of 100.
For example, 50% means 50 out of 100, which can be simplified to ½. Similarly, 25% is equivalent to ¼, and 75% is equivalent to ¾. Understanding this fundamental concept is key to mastering percentage calculations.
Calculating 4 out of 17 as a Percentage: Method 1 - The Fraction Method
This is the most straightforward approach. We'll convert the given statement "4 out of 17" into a fraction and then convert that fraction into a percentage.
Step 1: Express as a fraction:
The statement "4 out of 17" can be written as the fraction 4/17.
Step 2: Convert the fraction to a decimal:
To convert a fraction to a decimal, we divide the numerator (the top number) by the denominator (the bottom number):
4 ÷ 17 ≈ 0.23529
Step 3: Convert the decimal to a percentage:
To convert a decimal to a percentage, we multiply the decimal by 100 and add the "%" symbol:
0.23529 × 100 ≈ 23.53%
Therefore, 4 out of 17 is approximately 23.53%. Note that we rounded the result to two decimal places for practical purposes.
Calculating 4 out of 17 as a Percentage: Method 2 - The Proportion Method
This method utilizes the concept of proportions to solve for the unknown percentage.
We can set up a proportion:
4/17 = x/100
Where 'x' represents the percentage we want to find.
To solve for 'x', we cross-multiply:
17x = 400
Now, divide both sides by 17:
x = 400/17 ≈ 23.53
Therefore, 4 out of 17 is approximately 23.53%. This method confirms the result obtained using the fraction method.
Understanding the Significance of Rounding
In our calculations, we rounded the decimal 0.23529 to 0.2353 before converting it to a percentage. The level of rounding depends on the context and the required precision. For many practical applications, rounding to two decimal places (e.g., 23.53%) is sufficient. However, for scientific or financial calculations where high accuracy is crucial, you might need to round to more decimal places or use the exact decimal value.
Real-World Applications of Percentage Calculations
Understanding how to calculate percentages has numerous practical applications in daily life and various professional settings:
-
Finance: Calculating interest rates, discounts, tax rates, profit margins, and investment returns all involve percentage calculations. For instance, understanding the percentage increase or decrease in your investment portfolio is crucial for financial planning.
-
Academics: Grade calculations, test scores, and statistics in research papers frequently use percentages to represent data effectively. For example, if you answered 4 out of 17 questions correctly on a quiz, your score would be approximately 23.53%.
-
Retail: Discounts and sales are often expressed as percentages. A "20% off" sale indicates a 20% reduction in the original price. Understanding these percentages helps consumers make informed purchasing decisions.
-
Science and Statistics: Percentages are used extensively in scientific research and data analysis to represent proportions, probabilities, and error margins. For instance, expressing experimental results as percentages helps researchers communicate their findings accurately.
-
Health and Fitness: Body fat percentage, calorie intake as a percentage of daily needs, and progress towards fitness goals are all frequently expressed using percentages.
-
Everyday Life: Tip calculations in restaurants, splitting bills, calculating the percentage of a budget allocated to different expenses, and even understanding weather forecasts (e.g., a 20% chance of rain) all involve percentage calculations.
Related Percentage Calculations
Mastering the calculation of "4 out of 17" opens the door to understanding other related percentage calculations. Let's explore a few:
-
Calculating the percentage of a larger number: If you wanted to find 23.53% of a larger number (say, 500), you would multiply 500 by 0.2353 (the decimal equivalent of 23.53%). This would give you the value that represents 23.53% of 500.
-
Finding the original number from a percentage: If you know that a certain amount represents a specific percentage of an unknown original number, you can use algebraic equations to solve for the original number.
-
Calculating percentage change: This involves finding the percentage increase or decrease between two numbers. The formula for percentage change is: [(New Value - Old Value) / Old Value] x 100.
-
Calculating percentage points: Percentage points represent the arithmetic difference between two percentages, unlike percentage change which represents a relative difference. For example, an increase from 20% to 25% is a 5 percentage point increase, not a 25% increase.
Improving Your Percentage Calculation Skills
To further hone your percentage calculation skills, consider practicing with various examples. Start with simple fractions and gradually progress to more complex calculations. Utilize online calculators or practice problems to build your confidence and accuracy. Regular practice will help you internalize the methods and improve your speed and efficiency in performing these calculations.
Conclusion
Calculating "4 out of 17 as a percentage" is a straightforward process that can be accomplished through various methods, such as the fraction method or the proportion method. Understanding this fundamental calculation is crucial for numerous applications across various fields. By mastering these methods and exploring related percentage calculations, you will significantly enhance your numerical literacy and ability to interpret and communicate data effectively in both personal and professional settings. Remember, consistent practice and real-world application are key to solidifying your understanding of percentages and their widespread significance.
Latest Posts
Latest Posts
-
Early Stage Ovarian Cancer Ultrasound Color Doppler
May 27, 2025
-
How Does The Hartsfield Jackson Atlanta International Airport Relate To Science
May 27, 2025
-
What Is The Cure For Eda
May 27, 2025
-
What Address Is Used For Ethernet Broadcasts
May 27, 2025
-
Why Do Black People Have Bigger Lips
May 27, 2025
Related Post
Thank you for visiting our website which covers about 4 Out Of 17 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.