4/5 Divided By 6/7 In Simplest Form
listenit
May 09, 2025 · 5 min read
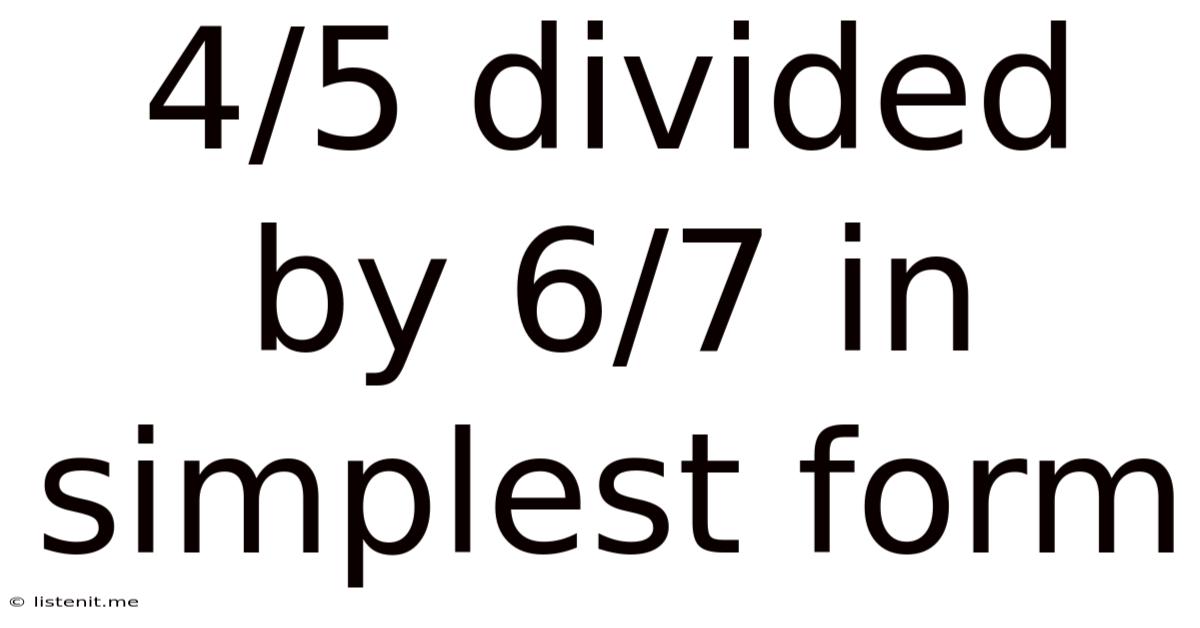
Table of Contents
4/5 Divided by 6/7 in Simplest Form: A Comprehensive Guide
Dividing fractions can seem daunting at first, but with a clear understanding of the process, it becomes straightforward. This article will meticulously guide you through calculating 4/5 divided by 6/7, explaining the steps involved and providing valuable insights into simplifying fractions. We'll delve into the underlying principles, explore alternative methods, and offer practical examples to solidify your understanding. By the end, you'll not only know the answer but also possess a robust understanding of fraction division.
Understanding Fraction Division
Before diving into the specific problem, let's establish a solid foundation in fraction division. The core concept revolves around the reciprocal. When we divide by a fraction, we essentially multiply by its reciprocal. The reciprocal of a fraction is simply the fraction inverted; the numerator becomes the denominator, and the denominator becomes the numerator.
Key Concept: Dividing by a fraction is the same as multiplying by its reciprocal.
For example, dividing by ½ is the same as multiplying by 2/1 (or simply 2). This fundamental principle is the cornerstone of solving any fraction division problem.
Step-by-Step Solution: 4/5 ÷ 6/7
Now, let's tackle the problem at hand: 4/5 divided by 6/7.
Step 1: Find the Reciprocal of the Second Fraction
The second fraction is 6/7. Its reciprocal is 7/6.
Step 2: Rewrite the Division as Multiplication
Our problem now transforms from 4/5 ÷ 6/7 to 4/5 × 7/6.
Step 3: Multiply the Numerators and Denominators
Multiply the numerators together: 4 × 7 = 28 Multiply the denominators together: 5 × 6 = 30
This gives us the fraction 28/30.
Step 4: Simplify the Fraction
The fraction 28/30 is not in its simplest form. To simplify, we need to find the greatest common divisor (GCD) of the numerator (28) and the denominator (30). The GCD is the largest number that divides both 28 and 30 without leaving a remainder.
Finding the GCD can be done through several methods:
-
Listing Factors: List the factors of 28 (1, 2, 4, 7, 14, 28) and the factors of 30 (1, 2, 3, 5, 6, 10, 15, 30). The greatest common factor is 2.
-
Prime Factorization: Break down 28 and 30 into their prime factors:
- 28 = 2 × 2 × 7
- 30 = 2 × 3 × 5
The common prime factor is 2. Therefore, the GCD is 2.
Step 5: Divide the Numerator and Denominator by the GCD
Divide both the numerator (28) and the denominator (30) by the GCD (2):
28 ÷ 2 = 14 30 ÷ 2 = 15
This simplifies the fraction to 14/15.
Therefore, 4/5 divided by 6/7 in its simplest form is 14/15.
Alternative Methods: Visualizing Fraction Division
While the reciprocal method is efficient, visualizing fraction division can enhance understanding. Consider using area models or number lines.
Area Model: Imagine a rectangle representing 4/5. Dividing this by 6/7 involves figuring out how many 6/7 units fit into 4/5. This visual approach can be helpful for grasping the concept, although it might be less practical for complex fractions.
Real-World Applications: Why is Fraction Division Important?
Understanding fraction division isn't just an academic exercise; it's a crucial skill with numerous real-world applications:
-
Cooking and Baking: Scaling recipes up or down requires accurate fraction division. If a recipe calls for 2/3 cup of flour and you want to make half the recipe, you need to divide 2/3 by 2.
-
Sewing and Crafting: Cutting fabric or other materials often involves precise fractional measurements. Dividing lengths of material accurately is essential for creating projects that fit correctly.
-
Construction and Engineering: Many construction and engineering projects rely on precise measurements, requiring calculations with fractions and division. Understanding fraction division ensures accuracy in these projects.
-
Finance: Managing budgets and investments involves working with fractions and percentages. Dividing fractions helps in understanding proportional relationships in financial contexts.
Expanding on Fraction Simplification: Strategies and Techniques
Simplifying fractions is a fundamental skill in mathematics, and mastering it improves accuracy and efficiency in calculations. Here are some key strategies and techniques:
-
Finding the Greatest Common Divisor (GCD): As demonstrated earlier, finding the GCD is crucial for simplifying fractions to their lowest terms. Methods like listing factors and prime factorization are effective ways to determine the GCD.
-
Using Prime Factorization: Expressing numbers as products of their prime factors provides a systematic approach to finding the GCD. This method is particularly useful for larger numbers.
-
Euclidean Algorithm: The Euclidean algorithm is a highly efficient method for finding the GCD of two numbers, especially when dealing with larger numbers. It involves repeatedly applying the division algorithm until the remainder is zero.
-
Simplifying Fractions with Variables: The principles of simplification extend to fractions with variables. Factoring the numerator and denominator and canceling common factors are key strategies.
Troubleshooting Common Mistakes in Fraction Division
Even experienced mathematicians can make mistakes when dividing fractions. Here's a look at common errors and how to avoid them:
-
Flipping the Wrong Fraction: Remember, only the second (divisor) fraction is flipped to its reciprocal. Flipping the first fraction will lead to an incorrect answer.
-
Incorrect Multiplication: Errors in multiplying the numerators and denominators after converting to multiplication can occur. Double-check your calculations carefully.
-
Failing to Simplify: Leaving the answer in an unsimplified form is a common mistake. Always simplify the final fraction to its lowest terms.
-
Misunderstanding the Concept: Ensure a thorough understanding of the underlying principles of fraction division before tackling complex problems.
Conclusion: Mastering Fraction Division
Dividing fractions, though initially challenging, becomes a manageable task with practice and a clear understanding of the underlying principles. The step-by-step approach, combined with understanding the concept of reciprocals and simplifying fractions, empowers you to confidently solve these types of problems. By mastering fraction division, you enhance your mathematical skills and gain a valuable tool applicable in various real-world scenarios. Remember to practice regularly, utilize different methods to deepen your understanding, and always double-check your work to minimize errors. With consistent effort, fraction division will become second nature.
Latest Posts
Latest Posts
-
In Some Cells Mitosis Occurs Without Cytokinesis
May 09, 2025
-
1 To The Power Of 8
May 09, 2025
-
Differentiate Between Cell Wall And Cell Membrane
May 09, 2025
-
An Electron Cannot Have The Quantum Numbers
May 09, 2025
-
Common Factors Of 16 And 48
May 09, 2025
Related Post
Thank you for visiting our website which covers about 4/5 Divided By 6/7 In Simplest Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.