4/5 Divided By 1/3 In Fraction Form
listenit
May 09, 2025 · 5 min read
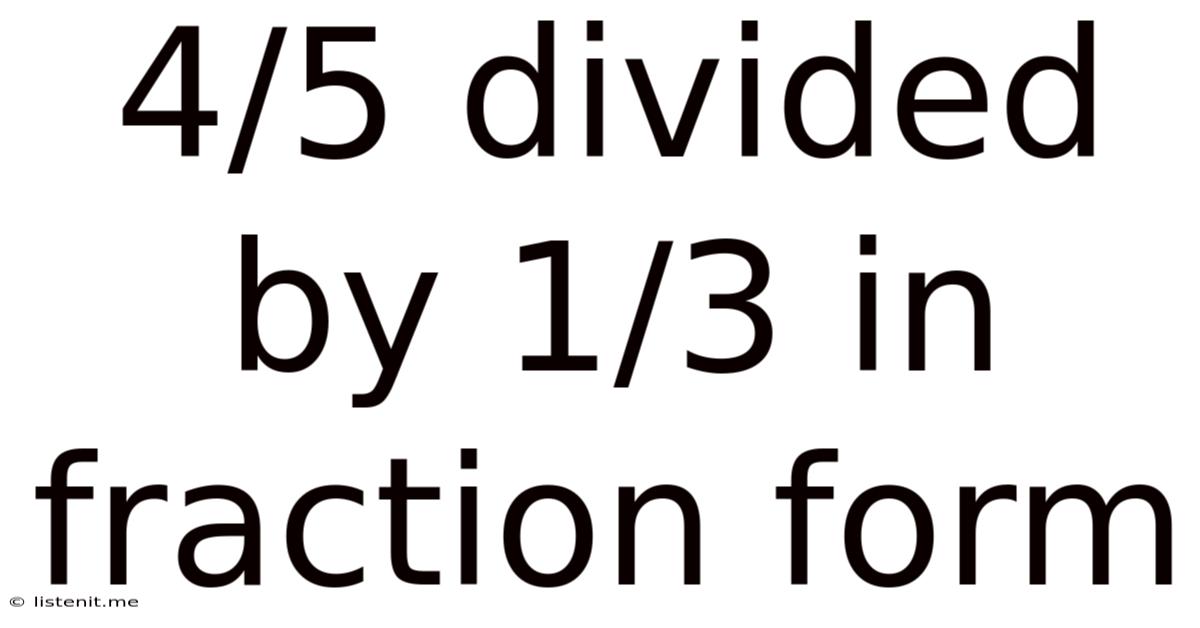
Table of Contents
4/5 Divided by 1/3 in Fraction Form: A Comprehensive Guide
Dividing fractions can seem daunting, but with a clear understanding of the process, it becomes straightforward. This article will thoroughly explore how to divide 4/5 by 1/3, explaining the concept in detail, providing step-by-step solutions, and offering various approaches to solidify your understanding. We'll also delve into the underlying principles and explore related concepts to build a strong foundation in fraction arithmetic.
Understanding Fraction Division
The core concept behind dividing fractions revolves around the idea of finding out "how many times" one fraction fits into another. When we divide 4/5 by 1/3, we're essentially asking: "How many times does 1/3 fit into 4/5?"
This differs from multiplying fractions. Multiplication finds the product of two fractions, while division finds how many times one fraction is contained within the other.
The Reciprocal Method: The Standard Approach
The most common method for dividing fractions involves using the reciprocal. The reciprocal of a fraction is simply the fraction flipped upside down. For example, the reciprocal of 1/3 is 3/1 (or simply 3).
Here's how to solve 4/5 divided by 1/3 using this method:
-
Find the reciprocal of the second fraction: The reciprocal of 1/3 is 3/1.
-
Change the division to multiplication: Replace the division sign (÷) with a multiplication sign (×).
-
Multiply the first fraction by the reciprocal of the second fraction:
(4/5) ÷ (1/3) = (4/5) × (3/1)
-
Multiply the numerators (top numbers) together: 4 × 3 = 12
-
Multiply the denominators (bottom numbers) together: 5 × 1 = 5
-
Simplify the result: The resulting fraction is 12/5. This can be expressed as a mixed number: 2 2/5.
Therefore, 4/5 divided by 1/3 equals 12/5 or 2 2/5.
Visualizing the Division: A Pictorial Approach
Imagine you have a pizza cut into 5 equal slices. You have 4 of these slices (4/5 of the pizza). Now, imagine you want to divide this 4/5 into portions that are each 1/3 of a pizza. How many of these 1/3 portions can you get from your 4/5?
This visual representation helps grasp the concept of fraction division. While not a formal calculation method, it provides an intuitive understanding of what's happening mathematically.
Alternative Approaches: Understanding the Underlying Principles
While the reciprocal method is efficient, understanding the underlying principles strengthens your grasp of fraction division. Let's explore a slightly different approach:
-
Find a common denominator: A common denominator for 5 and 3 is 15.
-
Convert the fractions to equivalent fractions with the common denominator:
4/5 becomes 12/15 (multiply numerator and denominator by 3) 1/3 becomes 5/15 (multiply numerator and denominator by 5)
-
Rewrite the division problem: The problem now becomes: (12/15) ÷ (5/15)
-
Divide the numerators: 12 ÷ 5 = 12/5
This approach highlights the division of the numerators after ensuring the fractions have the same denominator. It’s less efficient than the reciprocal method, but illuminates the underlying concept of comparing parts of a whole.
Applying Fraction Division in Real-World Scenarios
Fraction division appears frequently in everyday situations:
-
Cooking: If a recipe calls for 1/3 cup of sugar and you have 4/5 of a cup, how many times can you make the recipe? (Answer: 2 2/5 times – you can make the recipe twice with some sugar left over).
-
Sewing: If you need 1/3 yard of fabric for a project and you have 4/5 of a yard, how many projects can you complete? (Answer: 2 2/5 projects).
-
Construction: If a task requires 1/3 of a day and you have 4/5 of a day available, how many tasks can you complete? (Answer: 2 2/5 tasks).
These examples demonstrate the practical application of dividing fractions.
Further Exploration: Complex Fraction Division
Let's expand our understanding to tackle more complex scenarios involving nested or complex fractions.
Example: (4/5) ÷ (2/3 ÷ 1/2)
In this example, we have a nested division within the problem. To solve this, follow the order of operations (PEMDAS/BODMAS), performing the division within the parentheses first:
-
Inner Division: (2/3) ÷ (1/2) = (2/3) × (2/1) = 4/3
-
Outer Division: (4/5) ÷ (4/3) = (4/5) × (3/4) = 12/20 = 3/5
Therefore, (4/5) ÷ (2/3 ÷ 1/2) = 3/5.
Example: ( (4/5)/(1/3) ) / (1/2)
Here, the fraction is more complex due to the placement of the division signs. We still follow the order of operations. Let's tackle this step by step:
-
Innermost Division: (4/5) ÷ (1/3) = (4/5) × (3/1) = 12/5
-
Outer Division: (12/5) ÷ (1/2) = (12/5) × (2/1) = 24/5
Therefore, ( (4/5)/(1/3) ) / (1/2) = 24/5 or 4 4/5.
Mastering Fraction Division: Tips and Practice
Mastering fraction division requires consistent practice. Here are some tips:
-
Practice regularly: The more you practice, the more comfortable you'll become with the process.
-
Visualize the problem: Use diagrams or real-world examples to aid your understanding.
-
Break down complex problems: For complex fraction problems, break them into smaller, manageable steps.
-
Check your answers: Always check your answers to ensure accuracy.
-
Utilize online resources: Many websites and apps offer practice problems and tutorials on fraction division.
By consistently practicing and understanding the underlying principles, you'll build confidence and mastery in solving fraction division problems. Remember, the key is to practice regularly and utilize different techniques to solidify your understanding. The more you work with fractions, the easier they will become.
Latest Posts
Latest Posts
-
What Is One Fifth In Decimal Form
May 09, 2025
-
Eight More Than Twice A Number Is Eight
May 09, 2025
-
Greatest Common Factor Of 12 And 60
May 09, 2025
-
How To Find An Equation Of A Line Parallel
May 09, 2025
-
How Many Real Solutions Does The System Of Equations Have
May 09, 2025
Related Post
Thank you for visiting our website which covers about 4/5 Divided By 1/3 In Fraction Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.