4 5 Divided By 1 2
listenit
May 25, 2025 · 5 min read
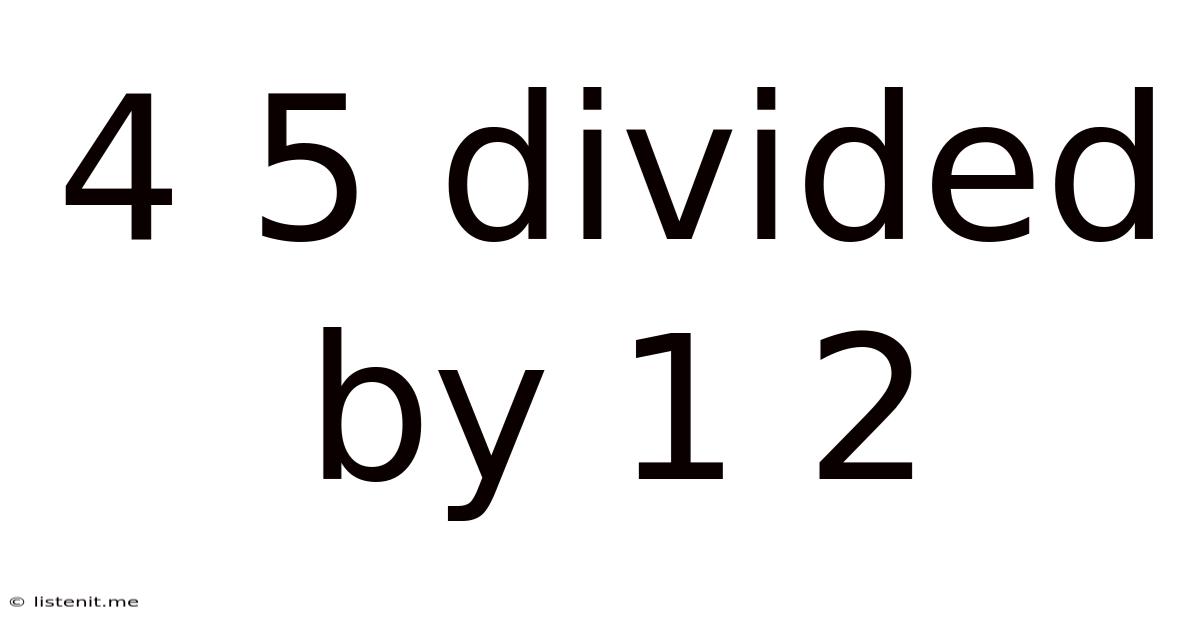
Table of Contents
4/5 Divided by 1/2: A Deep Dive into Fraction Division
Dividing fractions can seem daunting, but with a clear understanding of the underlying principles, it becomes a straightforward process. This article will thoroughly explore the division of 4/5 by 1/2, explaining the method, providing alternative approaches, and extending the concept to more complex scenarios. We'll also delve into the practical applications of fraction division in everyday life and various fields.
Understanding Fraction Division: The "Keep, Change, Flip" Method
The most common method for dividing fractions is the "keep, change, flip" (or "keep, switch, flip") method. This technique simplifies the division process by transforming it into a multiplication problem.
Here's how it works:
-
Keep: Keep the first fraction exactly as it is. In our case, this is 4/5.
-
Change: Change the division sign (÷) to a multiplication sign (×).
-
Flip: Flip (or find the reciprocal of) the second fraction. The reciprocal of 1/2 is 2/1 (or simply 2).
Therefore, 4/5 ÷ 1/2 becomes 4/5 × 2/1.
Performing the Multiplication
Now that we've transformed the division problem into a multiplication problem, we can proceed with the calculation:
4/5 × 2/1 = (4 × 2) / (5 × 1) = 8/5
This improper fraction, 8/5, can be converted into a mixed number:
8 ÷ 5 = 1 with a remainder of 3. Therefore, 8/5 = 1 3/5.
So, 4/5 divided by 1/2 equals 1 3/5.
Alternative Approaches: Visualizing Fraction Division
While the "keep, change, flip" method is efficient, visualizing fraction division can provide a deeper understanding of the concept. Let's consider the problem geometrically:
Imagine a rectangle representing the whole (1). Dividing this rectangle into 5 equal parts gives us sections representing 1/5 each. Four of these sections represent 4/5.
Now, consider dividing 4/5 into halves (1/2). This means we want to find out how many halves fit into 4/5. If we divide each of the four 1/5 sections in half, we get 8 smaller sections, each representing 1/10. Since each 1/2 is equivalent to 5/10, we can see that we have 8/10, which simplifies to 4/5. However, this visual approach isn't directly showing the division of 4/5 by 1/2.
A more effective visual approach would involve representing 4/5 as a collection of objects. Let's say we have 4 pizzas, each cut into 5 slices. Dividing by 1/2 means we're finding out how many half-pizzas we have. We have 4 pizzas * 5 slices/pizza = 20 slices. Each half-pizza is 2.5 slices, so we have 20 slices / 2.5 slices/half-pizza = 8 half-pizzas. That's equivalent to 8/2 = 4 whole pizzas.
The discrepancy arises from a slightly different interpretation of the problem. The initial visual representation may not be directly suitable for all scenarios.
Applying the Concept: Real-World Examples
Fraction division appears in various aspects of daily life and specialized fields:
-
Cooking: A recipe calls for 4/5 cups of flour, but you only want to make half the recipe. You would divide 4/5 by 1/2 to find the amount of flour needed: 4/5 ÷ 1/2 = 8/5 = 1 3/5 cups.
-
Sewing: You have 4/5 yards of fabric and need to cut it into pieces that are 1/2 yard long. Dividing 4/5 by 1/2 tells you how many pieces you can cut: 1 3/5 pieces (meaning you can cut one full piece and a smaller piece that's 3/5 of a yard).
-
Construction: A project requires 4/5 of a ton of cement, and you want to spread the work over two days. Dividing 4/5 by 1/2 gives the amount needed for each day: 8/5 = 1 3/5 tons per day.
-
Engineering: In engineering calculations involving ratios, proportions, and scaling, fraction division is frequently employed.
-
Finance: When dealing with portions of investments or calculating fractional shares, fraction division becomes crucial.
Extending the Concept: Dividing More Complex Fractions
The "keep, change, flip" method applies to more complex fractions as well. For example:
(3/4) / (2/5) = (3/4) x (5/2) = 15/8 = 1 7/8
(1 1/2) / (2/3) = (3/2) / (2/3) = (3/2) x (3/2) = 9/4 = 2 1/4
Remember to convert any mixed numbers to improper fractions before applying the "keep, change, flip" method.
Addressing Potential Confusion: The Importance of Order
It's crucial to remember that fraction division is not commutative. This means that the order of the fractions matters. 4/5 ÷ 1/2 is not the same as 1/2 ÷ 4/5.
1/2 ÷ 4/5 = (1/2) x (5/4) = 5/8
Conclusion: Mastering Fraction Division
Mastering fraction division empowers you to tackle a wide range of mathematical problems effectively. The "keep, change, flip" method provides a simple and efficient approach, while visual representations can enhance understanding. Remember to apply the method consistently, paying attention to the order of fractions. With practice, fraction division will become second nature, enabling you to confidently solve problems in various contexts. Understanding this fundamental concept opens doors to more advanced mathematical concepts and applications in various fields. The ability to confidently and correctly divide fractions is a vital skill that enhances problem-solving capabilities across numerous disciplines and daily life situations. Therefore, dedicated practice and a clear understanding of the underlying principles are key to mastering this crucial arithmetic operation.
Latest Posts
Latest Posts
-
4 To The Power Of 15
May 26, 2025
-
What Is The Percentage Of 22 Out Of 30
May 26, 2025
-
How To Find Sides Of A Triangle With One Side
May 26, 2025
-
What Date Is 20 Weeks From Now
May 26, 2025
-
30 Days After October 2 2024
May 26, 2025
Related Post
Thank you for visiting our website which covers about 4 5 Divided By 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.