4/3 Divided By 2 In Fraction
listenit
May 18, 2025 · 5 min read
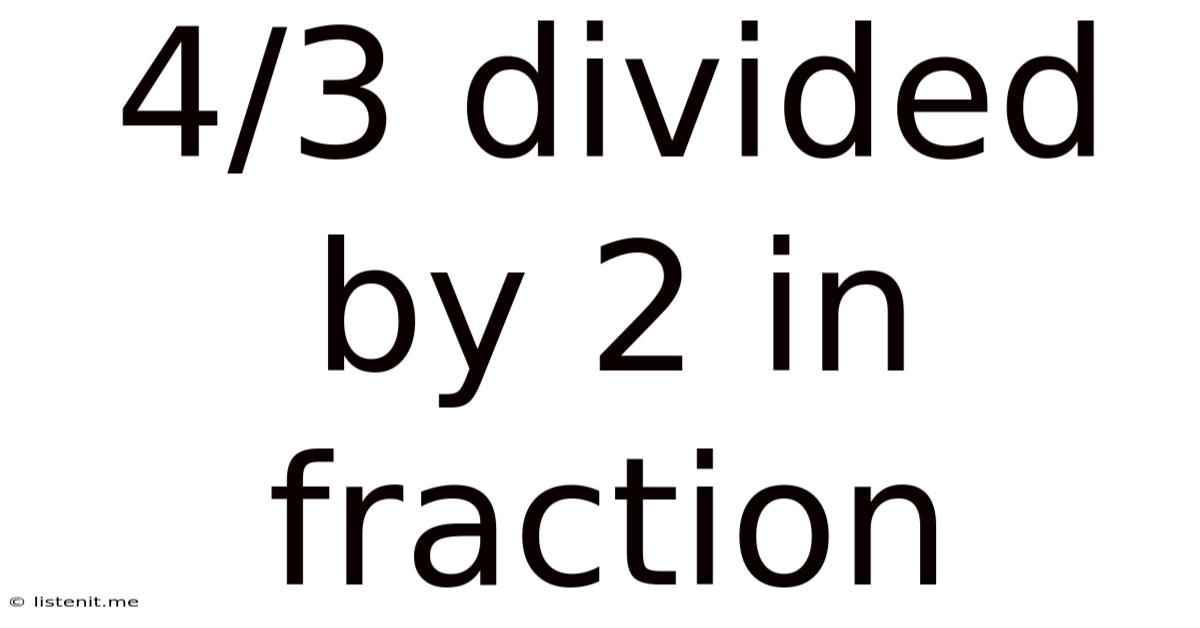
Table of Contents
4/3 Divided by 2: A Deep Dive into Fraction Division
Dividing fractions can seem daunting, but with a clear understanding of the process and a bit of practice, it becomes straightforward. This article will explore the seemingly simple problem of 4/3 divided by 2, breaking down the steps, explaining the underlying principles, and offering various approaches to solve similar problems. We'll also delve into the broader context of fraction division, providing you with a solid foundation for tackling more complex fraction calculations.
Understanding Fraction Division
Before tackling 4/3 divided by 2, let's establish the fundamental principle behind dividing fractions. The key concept is to reciprocate the divisor (the number you're dividing by) and then multiply. This means flipping the second fraction upside down and changing the division sign to a multiplication sign.
This seemingly simple rule stems from the definition of division itself. Division is essentially the inverse operation of multiplication. When we ask "What is 4/3 divided by 2?", we're essentially asking "What number, when multiplied by 2, equals 4/3?". The process of reciprocating and multiplying directly addresses this question.
Solving 4/3 Divided by 2: Step-by-Step
Let's now solve our problem: 4/3 ÷ 2.
Step 1: Rewrite the whole number as a fraction.
Every whole number can be expressed as a fraction with a denominator of 1. Therefore, we rewrite 2 as 2/1. Our problem now becomes:
4/3 ÷ 2/1
Step 2: Reciprocate the divisor (the second fraction).
We flip the second fraction, 2/1, upside down, making it 1/2.
Step 3: Change the division sign to a multiplication sign.
Our problem is now:
4/3 x 1/2
Step 4: Multiply the numerators (top numbers) and the denominators (bottom numbers).
Multiply the numerators: 4 x 1 = 4 Multiply the denominators: 3 x 2 = 6
This gives us the fraction 4/6.
Step 5: Simplify the fraction (if possible).
Both 4 and 6 are divisible by 2. Dividing both the numerator and the denominator by 2 simplifies the fraction to its lowest terms:
4/6 = 2/3
Therefore, 4/3 divided by 2 equals 2/3.
Alternative Approaches to Fraction Division
While the reciprocal-and-multiply method is the most common and generally preferred approach, there are alternative ways to think about fraction division. These alternative methods can enhance understanding and provide different perspectives.
Using the "Keep, Change, Flip" Method
This popular mnemonic device helps remember the steps:
- Keep the first fraction as it is (4/3).
- Change the division sign to a multiplication sign (x).
- Flip (reciprocate) the second fraction (2/1 becomes 1/2).
This method simplifies the process into easily memorable steps, reducing the chance of errors.
Visualizing with Models
For a more intuitive understanding, especially for beginners, you can use visual models like fraction circles or bars. Representing 4/3 and then dividing it into two equal parts visually demonstrates the result of 2/3. While not practical for complex problems, this method builds strong conceptual understanding.
Expanding on Fraction Division: More Complex Examples
Now that we've mastered 4/3 divided by 2, let's explore slightly more complex scenarios to solidify our understanding.
Example 1: Dividing a Mixed Number by a Fraction
Let's consider the problem: 1 1/2 ÷ 1/4.
Step 1: Convert the mixed number to an improper fraction.
1 1/2 is equivalent to (1 x 2 + 1)/2 = 3/2
Step 2: Apply the reciprocal-and-multiply method.
3/2 ÷ 1/4 becomes 3/2 x 4/1
Step 3: Multiply and simplify.
(3 x 4) / (2 x 1) = 12/2 = 6
Therefore, 1 1/2 divided by 1/4 equals 6.
Example 2: Dividing a Fraction by a Mixed Number
Let's tackle this problem: 2/5 ÷ 2 1/3.
Step 1: Convert the mixed number to an improper fraction.
2 1/3 is equivalent to (2 x 3 + 1)/3 = 7/3
Step 2: Apply the reciprocal-and-multiply method.
2/5 ÷ 7/3 becomes 2/5 x 3/7
Step 3: Multiply and simplify.
(2 x 3) / (5 x 7) = 6/35
Therefore, 2/5 divided by 2 1/3 equals 6/35.
Practical Applications of Fraction Division
Understanding fraction division isn't just about solving textbook problems. It has practical applications in various real-world scenarios:
- Cooking and Baking: Dividing recipes to adjust serving sizes often involves dividing fractions.
- Sewing and Crafts: Calculating fabric or material needs often requires fraction division.
- Construction and Engineering: Precise measurements in construction and engineering frequently involve fractions and their division.
- Data Analysis: Working with fractions and their divisions is essential in certain data analysis techniques.
Troubleshooting Common Mistakes
Several common errors can occur when dividing fractions. Being aware of these pitfalls can prevent inaccuracies:
- Forgetting to reciprocate: Failing to flip the second fraction is a frequent mistake. Always remember the crucial step of reciprocating the divisor.
- Incorrect multiplication: Errors in multiplying numerators and denominators are also common. Double-check your calculations to ensure accuracy.
- Not simplifying the fraction: Always simplify your final answer to its lowest terms for a complete and accurate solution.
Conclusion: Mastering Fraction Division
Dividing fractions, though initially appearing complex, becomes manageable with a systematic approach and understanding of the underlying principles. The reciprocal-and-multiply method, along with the "Keep, Change, Flip" mnemonic, provides a straightforward way to solve these problems. By practicing various examples and understanding the different approaches, you'll gain confidence and proficiency in handling fraction division, opening up a wider range of mathematical problem-solving capabilities. Remember to always check your work and simplify your answers to their lowest terms for accuracy. With consistent practice, fraction division will become second nature.
Latest Posts
Latest Posts
-
Risks Of Lung Biopsy In Elderly
Jun 05, 2025
-
What Is Worse For Liver Sugar Or Alcohol
Jun 05, 2025
-
How To Regulate Period On Spironolactone
Jun 05, 2025
-
Can Thc Be Absorbed Through Skin
Jun 05, 2025
-
Compared Human Full Grown Earless Monitor Lizard
Jun 05, 2025
Related Post
Thank you for visiting our website which covers about 4/3 Divided By 2 In Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.