4 3 Divided By 1 6
listenit
May 24, 2025 · 4 min read
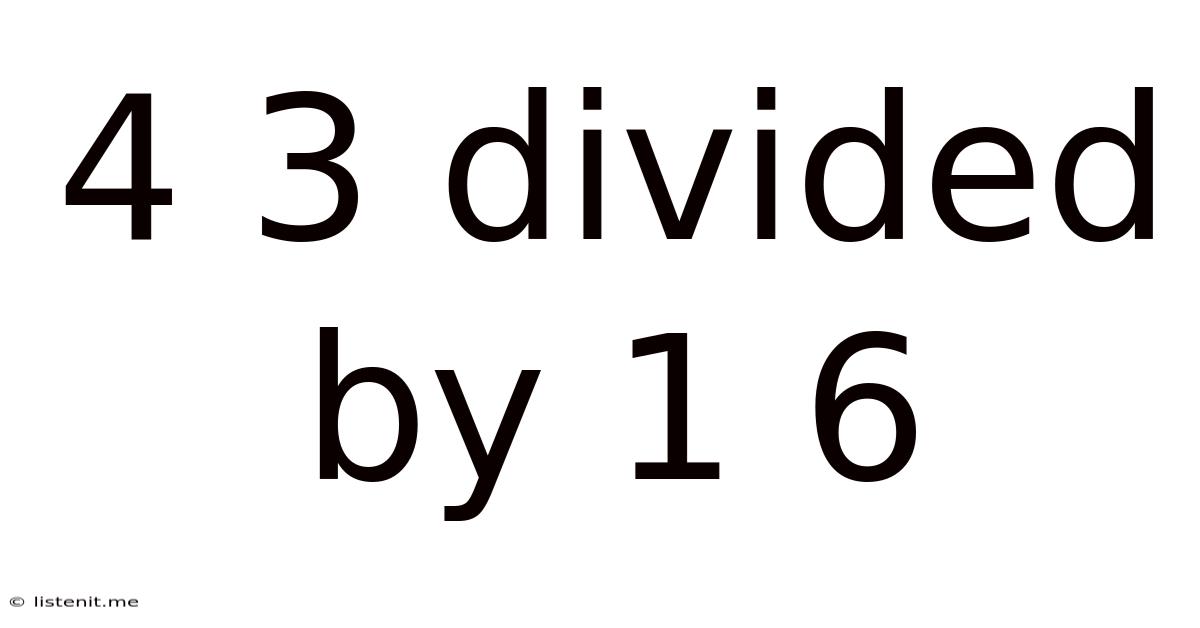
Table of Contents
Decoding 4 3/16: A Deep Dive into Fraction Division
This article will comprehensively explore the seemingly simple mathematical problem of dividing 4 3/16 by various numbers, delving into the fundamental principles of fraction manipulation, different solution methods, and real-world applications. We'll go beyond a simple answer, providing a thorough understanding of the process, enabling you to confidently tackle similar problems in the future.
Understanding Mixed Numbers and Improper Fractions
Before tackling the division, let's solidify our understanding of mixed numbers and improper fractions. A mixed number, like 4 3/16, combines a whole number (4) and a fraction (3/16). An improper fraction has a numerator larger than or equal to its denominator. To perform division effectively, it's often simpler to convert mixed numbers into improper fractions.
To convert 4 3/16 into an improper fraction:
- Multiply the whole number (4) by the denominator (16): 4 * 16 = 64
- Add the numerator (3) to the result: 64 + 3 = 67
- Keep the same denominator: 16
Therefore, 4 3/16 is equal to the improper fraction 67/16.
Dividing 4 3/16 by Different Numbers
Now let's explore how to divide 67/16 by various numbers. We'll examine different scenarios, demonstrating various approaches to ensure a complete understanding.
1. Dividing 4 3/16 by a Whole Number:
Let's divide 4 3/16 by 2. Using the improper fraction 67/16:
(67/16) ÷ 2 = 67/16 * (1/2) = 67/32
To convert this back to a mixed number:
- Divide the numerator (67) by the denominator (32): 67 ÷ 32 = 2 with a remainder of 3
- The whole number is 2.
- The remainder (3) becomes the numerator, and the denominator remains 32.
Therefore, 4 3/16 divided by 2 is 2 3/32.
2. Dividing 4 3/16 by a Fraction:
Let's divide 4 3/16 by 1/4. Again, using the improper fraction 67/16:
(67/16) ÷ (1/4) = 67/16 * (4/1) = 268/16
Simplifying the fraction by dividing both numerator and denominator by their greatest common divisor (4):
268/16 = 67/4
Converting to a mixed number:
67 ÷ 4 = 16 with a remainder of 3
Therefore, 4 3/16 divided by 1/4 is 16 3/4.
3. Dividing 4 3/16 by a Mixed Number:
Let's divide 4 3/16 by 2 1/2. First, convert both mixed numbers into improper fractions:
4 3/16 = 67/16 2 1/2 = 5/2
Now, perform the division:
(67/16) ÷ (5/2) = 67/16 * (2/5) = 134/80
Simplifying the fraction by dividing both numerator and denominator by their greatest common divisor (2):
134/80 = 67/40
Converting to a mixed number:
67 ÷ 40 = 1 with a remainder of 27
Therefore, 4 3/16 divided by 2 1/2 is 1 27/40.
4. Dividing 4 3/16 by a Decimal:
Let's divide 4 3/16 by 0.5. First, convert 4 3/16 to a decimal:
4 3/16 = 4 + (3/16) = 4 + 0.1875 = 4.1875
Now perform the division:
4.1875 ÷ 0.5 = 8.375
Alternatively, we can convert 0.5 to a fraction (1/2) and proceed as before:
(67/16) ÷ (1/2) = 67/16 * 2/1 = 134/16 = 67/8
Converting to a decimal:
67 ÷ 8 = 8.375
Therefore, 4 3/16 divided by 0.5 is 8.375.
Real-World Applications of Fraction Division
The ability to confidently divide fractions and mixed numbers is crucial in numerous real-world scenarios. Here are just a few examples:
- Baking and Cooking: Recipes often require precise measurements. If a recipe calls for a certain amount of an ingredient, and you want to make only half the recipe, you'll need to divide the quantities by 2, potentially involving fractions.
- Construction and Engineering: Accurate measurements are paramount in construction and engineering. Dividing lumber or calculating material requirements often involves fractions and mixed numbers.
- Sewing and Tailoring: Cutting fabric to exact specifications necessitates precise calculations, frequently utilizing fraction division.
- Finance and Budgeting: Dividing your budget into categories and tracking expenses often requires handling fractions or decimals representing proportions of your overall budget.
Advanced Concepts and Further Exploration
This article has covered the fundamentals of dividing 4 3/16 by various numbers. To delve deeper, consider exploring these advanced concepts:
- Complex Fractions: Fractions within fractions.
- Working with Negative Fractions: Understanding how to handle negative signs in fraction division.
- Recurring Decimals: Exploring the relationship between fractions and recurring decimals.
- Applications in Algebra: Using fraction division to solve algebraic equations.
Conclusion
Mastering fraction division is a cornerstone of mathematical literacy. By understanding the conversion between mixed numbers and improper fractions, and applying the correct steps for division, you can confidently tackle any problem involving fraction division. The methods illustrated in this article, along with the provided real-world examples, will empower you to approach similar calculations with assurance and precision. Remember to practice regularly to solidify your understanding and develop your skills. This comprehensive guide has provided a solid foundation; continue exploring and experimenting to build your expertise further. With consistent effort, you'll find that fraction division becomes an intuitive and manageable process.
Latest Posts
Latest Posts
-
What Is 10 Of 6 Million
May 24, 2025
-
Round 14 593 To The Nearest Ten
May 24, 2025
-
1 4 Of X Is 6
May 24, 2025
-
What Is 40 Percent Of 30 Dollars
May 24, 2025
-
19 Months Is How Many Years
May 24, 2025
Related Post
Thank you for visiting our website which covers about 4 3 Divided By 1 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.