3y 9x 12 Slope Intercept Form
listenit
May 11, 2025 · 4 min read
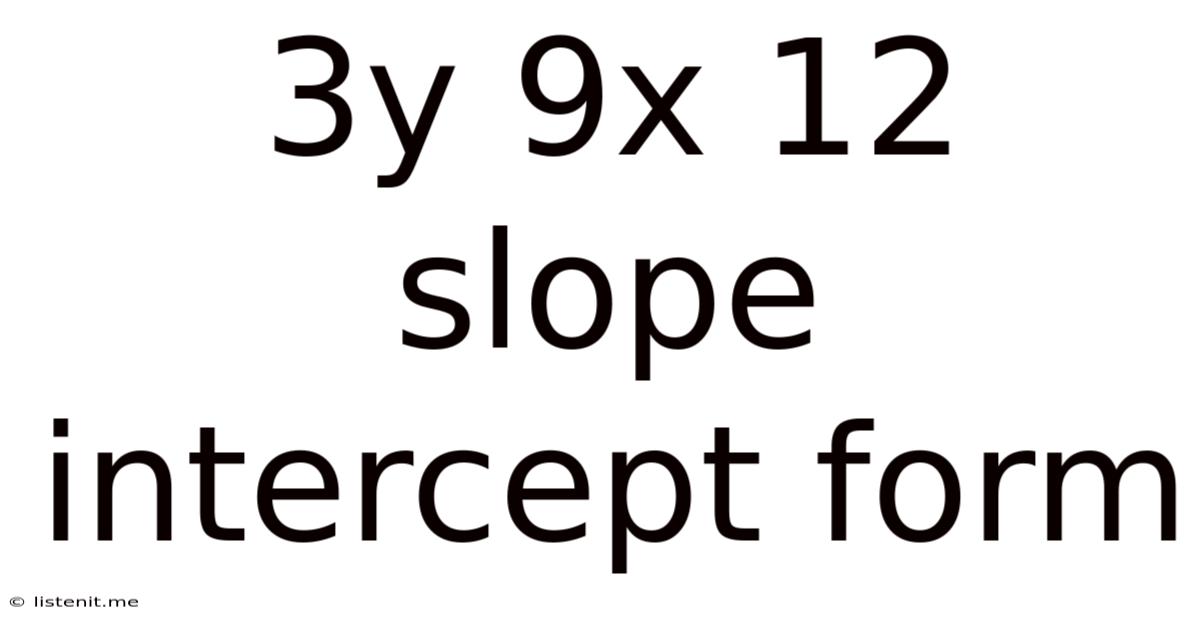
Table of Contents
Deconstructing the 3y + 9x = 12 Equation: A Deep Dive into Slope-Intercept Form
The equation 3y + 9x = 12 might seem deceptively simple at first glance. However, understanding its underlying structure and transforming it into slope-intercept form reveals crucial information about the line it represents. This article provides a comprehensive exploration of this equation, covering its conversion to slope-intercept form (y = mx + b), the significance of the slope (m) and y-intercept (b), graphing the line, and extending the understanding to related concepts.
Understanding Slope-Intercept Form (y = mx + b)
Before diving into the specifics of 3y + 9x = 12, let's solidify our understanding of the slope-intercept form of a linear equation: y = mx + b.
- y: Represents the dependent variable, typically plotted on the vertical axis of a graph.
- x: Represents the independent variable, typically plotted on the horizontal axis.
- m: Represents the slope of the line. The slope indicates the steepness and direction of the line. A positive slope means the line ascends from left to right, while a negative slope means it descends. The slope is calculated as the change in y divided by the change in x (rise over run).
- b: Represents the y-intercept, which is the point where the line intersects the y-axis (where x = 0).
Transforming 3y + 9x = 12 into Slope-Intercept Form
Our goal is to manipulate the equation 3y + 9x = 12 to fit the y = mx + b format. This involves isolating 'y' on one side of the equation. Let's break down the process step-by-step:
-
Subtract 9x from both sides: This moves the x term to the right side of the equation. 3y + 9x - 9x = 12 - 9x 3y = -9x + 12
-
Divide both sides by 3: This isolates 'y' and simplifies the equation. 3y / 3 = (-9x + 12) / 3 y = -3x + 4
Now we have the equation in slope-intercept form: y = -3x + 4.
Interpreting the Slope and Y-Intercept
By comparing our transformed equation to y = mx + b, we can extract valuable information:
-
Slope (m) = -3: This indicates a negative slope, meaning the line descends from left to right. The magnitude of the slope (3) tells us that for every 1 unit increase in x, y decreases by 3 units.
-
Y-intercept (b) = 4: This means the line intersects the y-axis at the point (0, 4).
Graphing the Line
Now that we have the slope and y-intercept, graphing the line is straightforward:
-
Plot the y-intercept: Start by plotting the point (0, 4) on the y-axis.
-
Use the slope to find another point: Since the slope is -3, we can move 1 unit to the right (increase x by 1) and 3 units down (decrease y by 3) from the y-intercept. This gives us the point (1, 1).
-
Draw the line: Draw a straight line through the two points (0, 4) and (1, 1). This line represents the equation 3y + 9x = 12.
Finding the X-intercept
The x-intercept is the point where the line intersects the x-axis (where y = 0). To find it, we can substitute y = 0 into the slope-intercept equation:
0 = -3x + 4 3x = 4 x = 4/3
Therefore, the x-intercept is (4/3, 0).
Parallel and Perpendicular Lines
Understanding the slope allows us to identify relationships between lines:
-
Parallel Lines: Parallel lines have the same slope but different y-intercepts. Any line parallel to y = -3x + 4 will have a slope of -3.
-
Perpendicular Lines: Perpendicular lines have slopes that are negative reciprocals of each other. The negative reciprocal of -3 is 1/3. Therefore, any line perpendicular to y = -3x + 4 will have a slope of 1/3.
Applications and Real-World Examples
Linear equations like 3y + 9x = 12 have numerous applications in various fields:
-
Physics: Describing the relationship between distance, speed, and time.
-
Economics: Modeling supply and demand curves.
-
Engineering: Representing the relationship between variables in design and construction.
-
Computer Science: Used in algorithms and data structures.
Extending the Understanding: Systems of Equations
The equation 3y + 9x = 12 can be part of a system of linear equations. Solving a system of equations involves finding the point (or points) where the lines intersect. For instance, consider the system:
3y + 9x = 12 y = 2x - 1
We can solve this system using substitution or elimination methods to find the coordinates where the two lines intersect.
Advanced Concepts: Linear Transformations and Matrices
At a more advanced level, the equation 3y + 9x = 12 can be represented using matrices and linear transformations. These concepts are fundamental in linear algebra and have wide applications in computer graphics, machine learning, and other fields.
Conclusion
The seemingly simple equation 3y + 9x = 12 reveals a wealth of information when analyzed through the lens of slope-intercept form. Understanding the slope, y-intercept, and the process of converting between different forms of linear equations is crucial for various mathematical and real-world applications. This article has provided a comprehensive exploration of this equation, equipping you with the knowledge to confidently tackle similar problems and delve into more advanced concepts in linear algebra. Remember to practice converting equations and graphing lines to solidify your understanding. The more you practice, the more intuitive these concepts will become.
Latest Posts
Latest Posts
-
Why Do Electric Field Lines Never Cross
May 13, 2025
-
1 10 As A Percent And Decimal
May 13, 2025
-
Can All Minerals Be A Gemstone
May 13, 2025
-
Multicellular Heterotrophs Without A Cell Wall
May 13, 2025
-
What Are The Gcf Of 48
May 13, 2025
Related Post
Thank you for visiting our website which covers about 3y 9x 12 Slope Intercept Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.