36 Out Of 45 Is What Percentage
listenit
May 09, 2025 · 4 min read
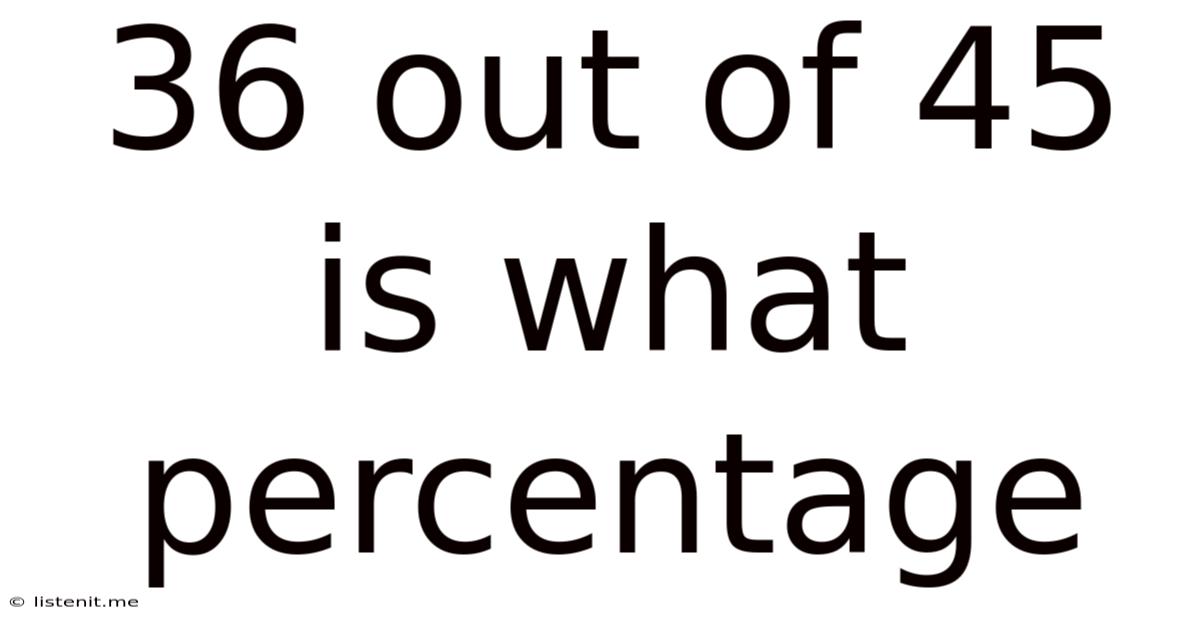
Table of Contents
36 out of 45 is What Percentage? A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill applicable across numerous fields, from everyday budgeting to complex scientific analyses. Understanding how to determine what percentage 36 out of 45 represents is not just about solving a single problem; it's about grasping the underlying principles that allow you to tackle countless similar calculations. This comprehensive guide will break down the process step-by-step, providing you with not only the answer but also a deep understanding of percentage calculations.
Understanding Percentages
Before diving into the specifics of 36 out of 45, let's solidify our understanding of percentages. A percentage is simply a fraction expressed as a number out of 100. The symbol "%" signifies "per hundred" or "out of 100." For example, 50% means 50 out of 100, which is equivalent to ½ or 0.5.
Calculating the Percentage: Step-by-Step
The process of calculating the percentage that 36 represents out of 45 involves three main steps:
Step 1: Set up the Fraction
First, we represent the problem as a fraction. The part (36) becomes the numerator, and the whole (45) becomes the denominator:
36/45
Step 2: Convert the Fraction to a Decimal
To convert the fraction to a decimal, we divide the numerator (36) by the denominator (45):
36 ÷ 45 = 0.8
Step 3: Convert the Decimal to a Percentage
Finally, we convert the decimal (0.8) to a percentage by multiplying it by 100 and adding the "%" symbol:
0.8 x 100 = 80%
Therefore, 36 out of 45 is 80%.
Alternative Calculation Methods
While the above method is the most straightforward, there are alternative approaches you can use, particularly helpful for mental calculations or when dealing with more complex scenarios.
Method 1: Simplifying the Fraction
Before dividing, we can simplify the fraction 36/45 by finding the greatest common divisor (GCD) of both numbers. The GCD of 36 and 45 is 9. Dividing both the numerator and the denominator by 9, we get:
36 ÷ 9 = 4 45 ÷ 9 = 5
This simplifies the fraction to 4/5. Now, converting 4/5 to a decimal:
4 ÷ 5 = 0.8
Then, converting the decimal to a percentage:
0.8 x 100 = 80%
This method demonstrates that simplifying fractions can make the division easier, especially when dealing with larger numbers.
Method 2: Using Proportions
Another approach involves using proportions. We can set up a proportion:
36/45 = x/100
Where 'x' represents the percentage we want to find. To solve for 'x', we cross-multiply:
45x = 3600
Then, divide both sides by 45:
x = 3600 ÷ 45 = 80
Therefore, x = 80%, confirming our previous result.
Practical Applications of Percentage Calculations
Understanding percentage calculations is crucial in many real-world situations. Here are some examples:
- Grade Calculation: If you answered 36 questions correctly out of 45 on a test, your score is 80%.
- Sales and Discounts: A store offering an 80% discount means you pay only 20% of the original price.
- Financial Analysis: Analyzing financial statements often involves calculating percentage changes in revenue, expenses, and profits.
- Scientific Research: Scientists frequently use percentages to represent data and analyze experimental results.
- Surveys and Polls: Results from surveys and polls are often presented as percentages.
Beyond the Basics: Handling More Complex Scenarios
While the example of 36 out of 45 provides a clear foundation, percentage calculations can become more intricate. Let's explore some more challenging scenarios:
- Calculating Percentage Increase or Decrease: This involves finding the percentage change between two values. For example, if sales increased from 100 to 120, the percentage increase is calculated as: [(120-100)/100] x 100% = 20%.
- Finding the Original Value: If a product is on sale for $60 after a 20% discount, the original price can be found by solving the equation: 0.8x = 60, where 'x' is the original price. Solving for x, we get x = $75.
- Calculating Compound Interest: Compound interest involves calculating interest on both the principal amount and accumulated interest. This requires more complex formulas.
- Working with Percentages of Percentages: This can involve nested percentage calculations, requiring careful attention to the order of operations.
Mastering these more advanced techniques requires practice and a solid understanding of the fundamental principles discussed earlier.
Tips for Accurate Percentage Calculations
- Double-check your work: Always review your calculations to avoid errors.
- Use a calculator: For complex calculations, a calculator can greatly improve accuracy and efficiency.
- Understand the context: Pay close attention to the specific context of the problem to ensure you're using the correct formula and interpreting the results appropriately.
- Practice regularly: Consistent practice is key to developing proficiency in percentage calculations.
Conclusion
Calculating the percentage that 36 represents out of 45—which is 80%—is a straightforward yet fundamental skill. This article not only provides the solution but also explores the underlying principles, alternative calculation methods, and practical applications of percentage calculations. By understanding these concepts, you'll be equipped to confidently tackle a wide range of percentage problems across various domains. Remember to practice regularly and utilize the tips provided to improve your accuracy and efficiency. With consistent effort, mastering percentage calculations will become second nature.
Latest Posts
Latest Posts
-
7 4 7 As A Improper Fraction
May 09, 2025
-
X 3 X 2 1 Graph
May 09, 2025
-
How Do You Write 1 5 As A Decimal
May 09, 2025
-
Do Weak Acids Have Weak Conjugate Bases
May 09, 2025
-
78 As A Fraction In Simplest Form
May 09, 2025
Related Post
Thank you for visiting our website which covers about 36 Out Of 45 Is What Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.