35 Out Of 38 As A Percentage
listenit
May 24, 2025 · 5 min read
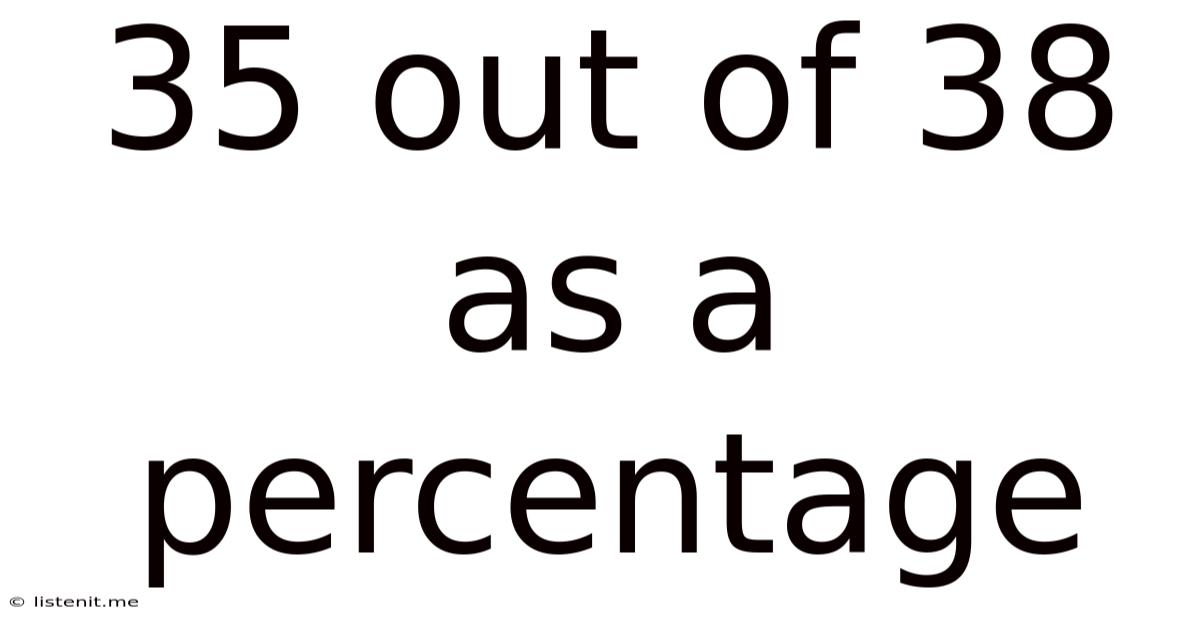
Table of Contents
35 out of 38 as a Percentage: A Comprehensive Guide to Percentage Calculations
Calculating percentages is a fundamental skill with wide-ranging applications in various aspects of life, from academic assessments to financial transactions and everyday decision-making. Understanding how to convert fractions and ratios into percentages is crucial for interpreting data, making comparisons, and understanding proportions. This comprehensive guide delves into the specifics of calculating "35 out of 38 as a percentage," offering various methods and explaining the underlying principles. We'll also explore related percentage calculations and provide practical examples to solidify your understanding.
Understanding Percentages: The Basics
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" literally means "out of one hundred." The symbol used to represent percentage is the percent sign, "%". Therefore, 25% is equivalent to 25/100 or 0.25.
Method 1: Using the Basic Percentage Formula
The most straightforward way to calculate 35 out of 38 as a percentage is using the fundamental percentage formula:
(Part / Whole) x 100% = Percentage
In this case:
- Part: 35 (the number of successful events or items)
- Whole: 38 (the total number of events or items)
Substituting these values into the formula:
(35 / 38) x 100% = 92.105%
Therefore, 35 out of 38 is approximately 92.11%.
Method 2: Converting the Fraction to a Decimal
Another approach involves first converting the fraction 35/38 into a decimal, and then multiplying by 100% to obtain the percentage.
- Divide the part by the whole: 35 ÷ 38 ≈ 0.92105
- Multiply the decimal by 100%: 0.92105 x 100% ≈ 92.11%
This method provides the same result as the previous one, confirming the accuracy of our calculation.
Understanding the Result: What Does 92.11% Mean?
The calculated 92.11% signifies that 35 represents approximately 92.11% of 38. This percentage can be interpreted in various contexts. For instance, if you scored 35 out of 38 on a test, your score would be 92.11%. Similarly, if 35 out of 38 products passed quality control, the pass rate would be 92.11%. The percentage provides a clear and concise way to represent the proportion.
Rounding and Significant Figures
In the calculations above, we rounded the result to two decimal places (92.11%). The level of precision needed depends on the context. In some situations, rounding to the nearest whole number (92%) might be sufficient, while others might require more decimal places for greater accuracy. Always consider the level of accuracy required for the specific application.
Practical Applications of Percentage Calculations
The ability to calculate percentages is essential in numerous real-world scenarios:
- Academic Performance: Calculating grades, test scores, and overall academic achievements.
- Financial Management: Computing interest rates, discounts, taxes, profits, and losses.
- Data Analysis: Interpreting statistical data, conducting surveys, and presenting research findings.
- Retail and Sales: Calculating discounts, profit margins, and sales tax.
- Everyday Life: Calculating tips, comparing prices, and understanding proportions in recipes or measurements.
Advanced Percentage Calculations: Related Problems
Let's explore some related percentage problems to further enhance your understanding:
1. Finding the Part:
If you know the percentage and the whole, you can calculate the part using this formula:
(Percentage/100) x Whole = Part
For example, what is 20% of 38?
(20/100) x 38 = 7.6
2. Finding the Whole:
If you know the percentage and the part, you can calculate the whole using this formula:
(Part / Percentage) x 100 = Whole
For example, if 35 is 92.11% of a certain number, what is that number?
(35 / 92.11) x 100 ≈ 38
3. Percentage Change:
Calculating percentage change (increase or decrease) is crucial in various contexts:
Percentage Change = [(New Value - Old Value) / Old Value] x 100%
For example, if a price increased from $20 to $25, the percentage increase is:
[(25 - 20) / 20] x 100% = 25%
4. Percentage Point Difference:
It's important to distinguish between percentage change and percentage point difference. A percentage point difference simply represents the difference between two percentages, while percentage change indicates the relative change between two values. For instance, an increase from 20% to 25% is a 5 percentage point difference, but a 25% percentage increase.
Using Technology for Percentage Calculations
While manual calculations are valuable for understanding the underlying principles, technology can greatly simplify the process, especially for more complex calculations or large datasets. Spreadsheets like Microsoft Excel and Google Sheets offer built-in functions for calculating percentages, making these computations fast and efficient. Calculators, both physical and digital, also provide easy access to percentage calculations.
Error Handling and Accuracy
When dealing with percentage calculations, accuracy is paramount. Pay close attention to the following:
- Rounding: Round numbers appropriately based on the required level of precision. Avoid premature rounding during intermediate calculations, as this can lead to inaccuracies in the final result.
- Significant Figures: Maintain an appropriate number of significant figures throughout your calculations to ensure accuracy.
- Unit Consistency: Ensure all units are consistent to avoid errors.
Conclusion: Mastering Percentage Calculations
Calculating percentages is a fundamental mathematical skill applicable in many areas of life. Understanding the basic formula, various calculation methods, and the ability to apply these techniques to different scenarios will significantly enhance your problem-solving skills and data interpretation abilities. By mastering percentage calculations, you will gain a stronger grasp of quantitative information and improve your decision-making in various contexts, both personal and professional. Remember to practice regularly to solidify your understanding and improve your speed and accuracy. This guide has served as a comprehensive introduction to percentage calculations, and by applying the principles outlined here, you'll be well-equipped to tackle any percentage-related problem with confidence.
Latest Posts
Latest Posts
-
How Many 2 5 Are In 1 1 2
May 24, 2025
-
What Is The Gcf Of 40 And 32
May 24, 2025
-
Greatest Common Factor Of 18 36 And 45
May 24, 2025
-
72k A Year Is How Much Biweekly
May 24, 2025
-
Greatest Common Factor Of 9 And 4
May 24, 2025
Related Post
Thank you for visiting our website which covers about 35 Out Of 38 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.