35 Of F Is 14 What Is F
listenit
May 12, 2025 · 4 min read
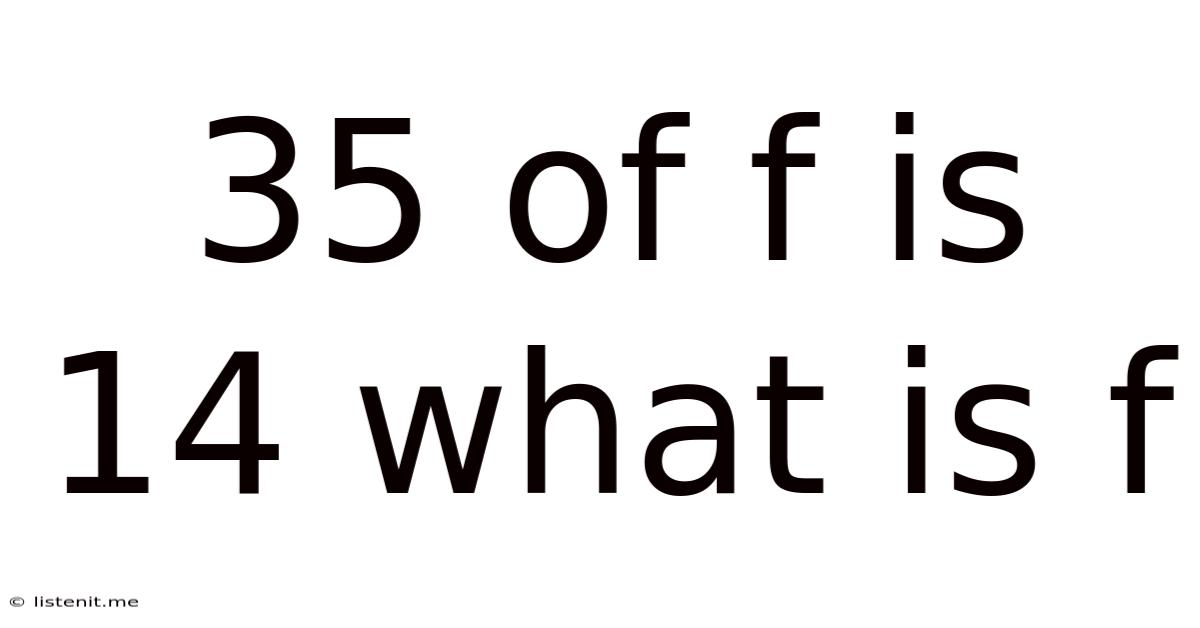
Table of Contents
35% of f is 14: What is f? Solving Percentage Problems
This article will guide you through solving the equation "35% of f is 14," explaining the process step-by-step and exploring various methods to arrive at the solution. We'll also delve into the broader context of percentage problems, offering tips and techniques for tackling similar equations in the future. Understanding percentages is crucial in many aspects of life, from calculating discounts and taxes to understanding financial statements and statistical data. This guide aims to empower you with the knowledge and skills to confidently solve percentage problems.
Understanding the Problem: 35% of f = 14
The core of the problem lies in translating the written statement into a mathematical equation. "35% of f is 14" can be written as:
0.35 * f = 14
This equation expresses the relationship between the percentage (35%), the unknown value (f), and the resulting value (14). Our goal is to isolate 'f' and find its numerical value.
Method 1: Solving using Algebraic Manipulation
This is the most straightforward method for solving the equation. We'll use basic algebraic techniques to isolate 'f'.
1. Convert the percentage to a decimal:
35% is equivalent to 0.35 (divide the percentage by 100).
2. Rewrite the equation:
Our equation becomes: 0.35f = 14
3. Isolate 'f':
To isolate 'f', we need to divide both sides of the equation by 0.35:
f = 14 / 0.35
4. Calculate the value of 'f':
Performing the division:
f = 40
Therefore, the value of 'f' is 40.
Method 2: Using Proportions
Proportions offer another approach to solve percentage problems. We can set up a proportion to represent the relationship between the percentage, the unknown value, and the given result.
1. Set up the proportion:
We can write the proportion as:
35/100 = 14/f
This proportion states that the ratio of 35 to 100 is equal to the ratio of 14 to f.
2. Cross-multiply:
Cross-multiplying the proportion gives us:
35f = 14 * 100
35f = 1400
3. Solve for 'f':
Divide both sides of the equation by 35:
f = 1400 / 35
f = 40
Again, we find that the value of 'f' is 40.
Method 3: Using the Percentage Formula
The basic percentage formula is:
(Part / Whole) * 100 = Percentage
In our case:
- The percentage is 35%
- The part is 14
- The whole is 'f' (what we want to find)
1. Substitute the values into the formula:
(14 / f) * 100 = 35
2. Solve for 'f':
1400 / f = 35
1400 = 35f
f = 1400 / 35
f = 40
Once more, we arrive at the solution: f = 40.
Verification of the Solution
Let's verify our solution by substituting f = 40 back into the original equation:
0.35 * 40 = 14
This confirms that our solution is correct.
Expanding the Understanding: Percentage Concepts
Understanding percentages goes beyond simply solving equations. Let's explore some key concepts:
Percentage Increase and Decrease
Percentage increase or decrease calculations are frequently encountered in various applications. These involve finding the change in a value as a percentage of the original value.
- Percentage Increase: [(New Value - Original Value) / Original Value] * 100
- Percentage Decrease: [(Original Value - New Value) / Original Value] * 100
Calculating Percentage of a Number
To calculate a percentage of a number, simply convert the percentage to a decimal and multiply it by the number. For example, 20% of 50 is 0.20 * 50 = 10.
Finding the Original Value after a Percentage Change
If you know the final value after a percentage increase or decrease, you can work backward to find the original value. This often requires using algebraic manipulation similar to the methods shown above.
Practical Applications of Percentage Calculations
Percentage calculations are essential in many real-world scenarios:
- Finance: Calculating interest rates, loan repayments, profits, and losses.
- Retail: Determining discounts, sales tax, and profit margins.
- Science: Expressing experimental results and statistical data.
- Everyday Life: Understanding tips, taxes, and comparing prices.
Tips for Solving Percentage Problems
- Clearly define the unknown: Identify what you're trying to find.
- Translate the problem into an equation: Convert the words into mathematical symbols.
- Use appropriate methods: Choose the most efficient method based on the problem's structure.
- Check your answer: Substitute the solution back into the original equation to verify its correctness.
- Practice regularly: The more you practice, the more confident and efficient you'll become.
Conclusion: Mastering Percentage Calculations
Solving "35% of f is 14" demonstrates the fundamental principles of percentage problems. By understanding the different methods and applying the key concepts discussed in this article, you can confidently tackle a wide range of percentage calculations encountered in various aspects of life. Remember to practice regularly, and you will master this essential mathematical skill. The ability to quickly and accurately calculate percentages is a valuable asset in both personal and professional contexts.
Latest Posts
Related Post
Thank you for visiting our website which covers about 35 Of F Is 14 What Is F . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.