35 Is 70 Percent Of What Number
listenit
May 10, 2025 · 5 min read
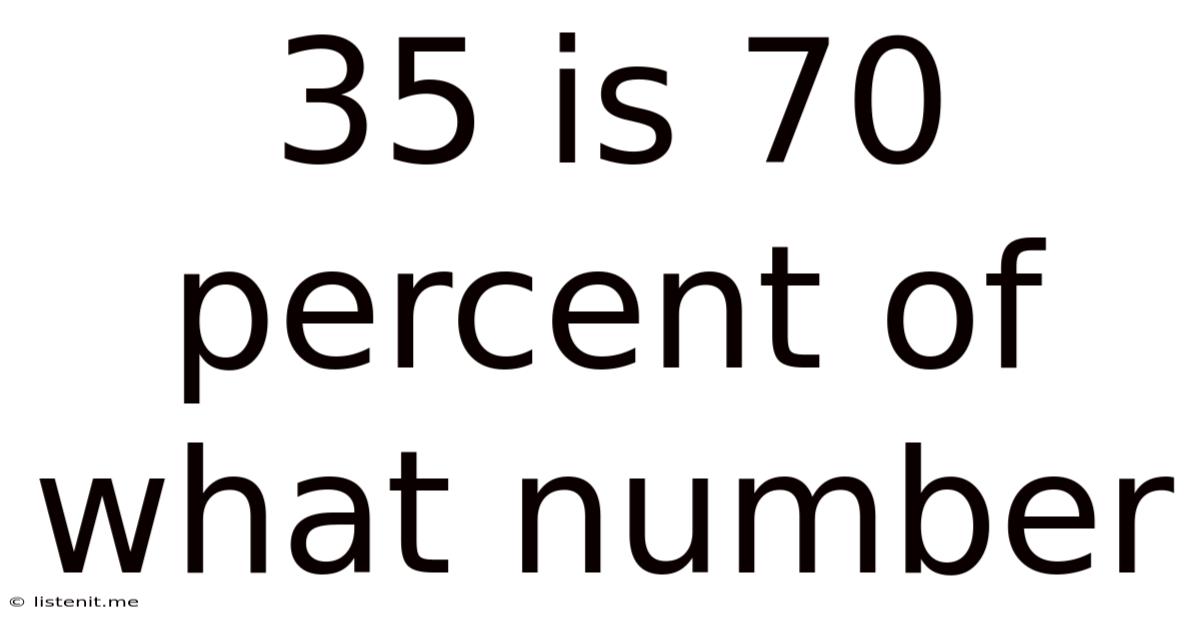
Table of Contents
35 is 70 Percent of What Number? A Comprehensive Guide to Percentage Calculations
Solving percentage problems is a fundamental skill applicable across various fields, from everyday budgeting to complex financial analysis. This article will delve into the solution of the problem "35 is 70 percent of what number?", explaining not only the answer but also the underlying principles and multiple methods for tackling similar percentage questions. We’ll explore different approaches, including the algebraic method, the unitary method, and the practical application of these techniques. We'll also touch on the importance of accurate percentage calculations in real-world scenarios.
Understanding the Problem: Deconstructing the Percentage
The question "35 is 70 percent of what number?" essentially asks us to find the whole when we know a part and the percentage that part represents. This is a common type of percentage problem. To solve it, we need to understand the relationship between the percentage, the part, and the whole.
Let's break down the elements:
- Part: This is the known value, which is 35 in this case.
- Percentage: This represents the proportion of the whole, expressed as a percentage (70%).
- Whole: This is the unknown value we need to find. Let's represent this with the variable 'x'.
Method 1: The Algebraic Approach
The most straightforward way to solve this problem is by setting up an algebraic equation. We can translate the problem into an equation as follows:
70% of x = 35
First, convert the percentage to a decimal by dividing by 100:
0.70x = 35
Now, solve for x by dividing both sides of the equation by 0.70:
x = 35 / 0.70
x = 50
Therefore, 35 is 70 percent of 50.
This method is precise and easily adaptable to different percentage problems. Simply replace the known values with the numbers from your specific problem, and you can solve for the unknown.
Method 2: The Unitary Method
The unitary method is a more intuitive approach, particularly useful for those less comfortable with algebra. It involves finding the value of 1% first, and then scaling up to find the value of 100%.
-
Find the value of 1%: If 70% of a number is 35, then we can find 1% by dividing 35 by 70:
35 / 70 = 0.5
This means 1% of the number is 0.5.
-
Find the value of 100%: To find the whole number (100%), multiply the value of 1% by 100:
0.5 * 100 = 50
Therefore, the whole number is 50. Again, we arrive at the same conclusion: 35 is 70 percent of 50.
The unitary method provides a step-by-step process that's easy to follow and understand, making it a valuable alternative to the algebraic method.
Method 3: Using Proportions
This method leverages the concept of ratios and proportions to solve percentage problems. We can set up a proportion to represent the relationship between the known values and the unknown value:
70/100 = 35/x
This equation states that the ratio of 70 to 100 (70%) is equal to the ratio of 35 to the unknown number (x). To solve for x, we cross-multiply:
70x = 35 * 100
70x = 3500
x = 3500 / 70
x = 50
Once again, we confirm that 35 is 70 percent of 50. This method highlights the proportional relationship inherent in percentage calculations.
Practical Applications of Percentage Calculations
Understanding percentage calculations is crucial in various real-world scenarios. Here are a few examples:
- Financial Calculations: Calculating discounts, interest rates, taxes, and profit margins all involve percentages. For example, determining the original price of an item after a 20% discount requires similar calculations to the problem we just solved.
- Data Analysis: Percentages are essential for representing data in reports, graphs, and charts. Understanding percentage changes helps in tracking trends and making informed decisions. For instance, calculating the percentage increase or decrease in sales revenue over time.
- Scientific Calculations: Many scientific experiments and studies involve analyzing data expressed as percentages. For example, determining the percentage of a particular element in a compound or calculating the success rate of a medical treatment.
- Everyday Life: We use percentages daily – calculating tips in restaurants, understanding sale prices, or figuring out the percentage of a task that's been completed.
Mastering percentage calculations ensures accurate and efficient problem-solving in these and many other areas.
Common Mistakes to Avoid
Several common errors can lead to inaccurate results when working with percentages. Let's address some of them:
- Incorrect Conversion: Failing to convert percentages to decimals (or fractions) before performing calculations is a major source of errors. Remember to always divide the percentage by 100 to obtain its decimal equivalent.
- Mixing Up Parts and Wholes: Carefully identify the part (known value) and the whole (unknown value) before setting up the equation or proportion. Confusion in these designations will lead to incorrect solutions.
- Arithmetic Errors: Simple arithmetic mistakes can significantly impact the outcome. Double-check your calculations to ensure accuracy. Use a calculator if necessary.
- Misinterpreting the Problem: Carefully read and understand the problem statement. Make sure you're correctly identifying what is being asked for.
Expanding Your Skills: More Complex Percentage Problems
While the problem "35 is 70 percent of what number?" provides a fundamental understanding of percentage calculations, more complex problems might involve:
- Multiple Percentages: Problems involving consecutive percentages (e.g., a 10% discount followed by a 5% discount) require a more nuanced approach.
- Percentage Increase/Decrease: Calculating the percentage increase or decrease between two values requires subtracting the values and then expressing this difference as a percentage of the original value.
- Compound Interest: Calculating compound interest involves applying a percentage repeatedly over a period of time, requiring a slightly more advanced formula.
By mastering the fundamental principles illustrated in this article, you’ll build a strong foundation to tackle more advanced percentage problems.
Conclusion: Mastering Percentages for Success
Solving percentage problems like "35 is 70 percent of what number?" is a valuable skill with widespread applications. Whether you're dealing with financial matters, analyzing data, or tackling everyday calculations, a solid understanding of percentages is essential. This article explored various methods – the algebraic method, the unitary method, and the proportions method – providing you with diverse tools to approach such problems effectively. By avoiding common mistakes and practicing regularly, you can build confidence and accuracy in your percentage calculations, paving the way for success in various aspects of life and work. Remember to practice regularly and apply these methods to a variety of problems to reinforce your understanding and build proficiency.
Latest Posts
Latest Posts
-
Do Bacteria Contain Dna Or Rna
May 10, 2025
-
How Many Protons Does B Have
May 10, 2025
-
Which State Of Matter Has The Slowest Moving Particles
May 10, 2025
-
How To Do Absolute Value On Ti 84 Plus Ce
May 10, 2025
-
1 8 To The Power Of
May 10, 2025
Related Post
Thank you for visiting our website which covers about 35 Is 70 Percent Of What Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.